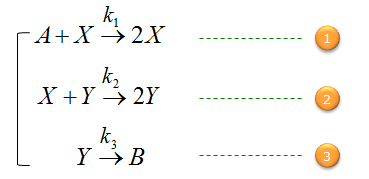|
Engineering Math - Differential Equation |
||
|
Chemical Reaction
One of the difficulties of modeling chemical reactions with differential equation would be that setting the governing equation is not always simple and intuitive. I would suggest you to do some further readings if you are interested in modeling chemical reactions more seriously.
Following table would help you with figuring out a governing equation that will be used for the example in this page. This table is from the reference linked here. I would strongly suggest you to read this reference because it would give you not only for setting up the governing equation but also for analysing a sequence of related chemical reactions at a system level.
NOTE : Before look into the derivation of the equation, it would be good to have some intuitive understandings on the solution of the differential equation for this model. Check out this page and see how the solution graph changes as the parameters in the equation changes.
Now let's look into an example. I got this example reaction sequence from the reference linked here and explained it in my way in this note.
Assume that you have a tank which contains the chemicals named A, X, Y, B and all of these are undergoing chemical reactions as shown below.
Your job is to build a set of differential equations predicting the concentration of each chemicals along with time.
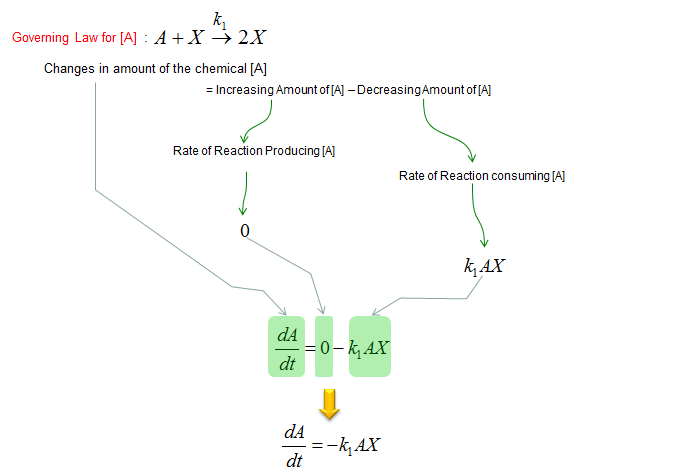
First, let's build a differential equation for the chemical A. To do this, first identify all the chemical reactions which either consumes or produce the chemical (i.e, identify all the chemical reactions in which the chemical A is involved). And then build a differential equation according to the governing equation as shown below.
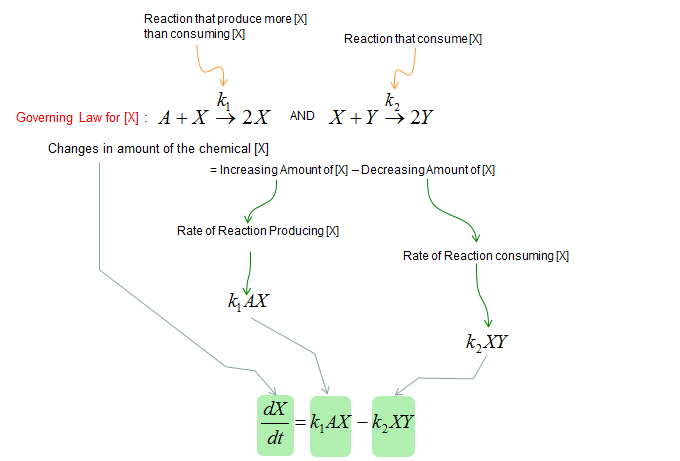
Next, let's build a differential equation for the chemical X. To do this, first identify all the chemical reactions which either consumes or produce the chemical (i.e, identify all the chemical reactions in which the chemical X is involved). And then build a differential equation according to the governing equation as shown below.
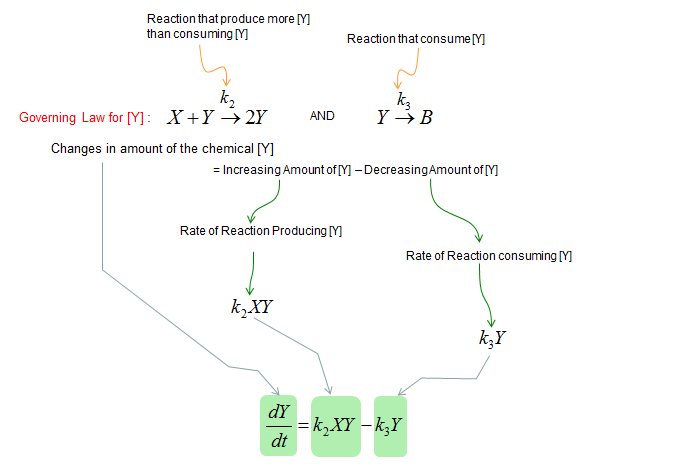
Next, let's build a differential equation for the chemical Y. To do this, first identify all the chemical reactions which either consumes or produce the chemical (i.e, identify all the chemical reactions in which the chemical Y is involved). And then build a differential equation according to the governing equation as shown below.
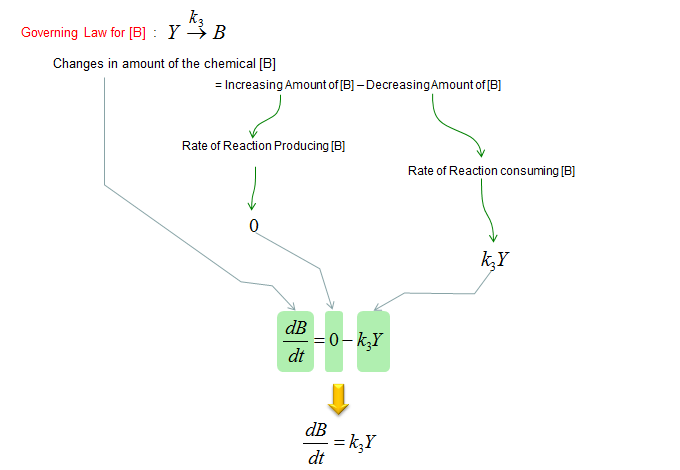
Next, let's build a differential equation for the chemical B. To do this, first identify all the chemical reactions which either consumes or produce the chemical (i.e, identify all the chemical reactions in which the chemical B is involved). And then build a differential equation according to the governing equation as shown below.
Now we got all the differential equations representing the concentration of each individual chemicals. The last step is to put all the equations together as a simulteneous equation as shown below.
NOTE : Even though it is not exactly same equation, I put the graphical solution of similar differential equation on this note in www.slide4math.com.
Reference :
[1] From Processes to ODEs by Chemistry (Luca Cardelli, Microsoft Research) [2] Math 231:Introduction to Ordinary Differential Equations (H. Finotti, The University of Tennessee) [3] 14.3: Concentration and Rates (Differential Rate Laws)
|
||