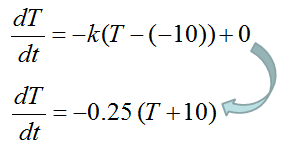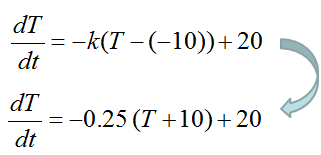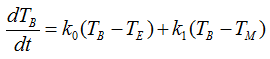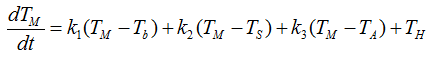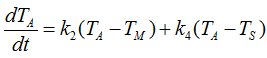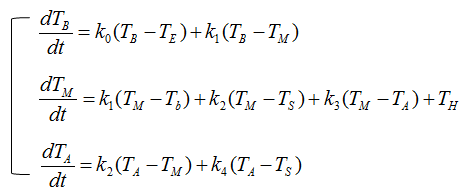In this section, I will show you some of the examples of building differential equations for cooling & heating. As I mentioned in Governing Equation page, the most important step for cooling/heating case as well is to figure out proper governing equation (governing law). The fundamentals of Cooling problem is based on Newton's Law of Cooling. (I will add some comments on this in my own words later when I have time, but for now I would suggest you to google some basics of Newton's Law of Cooling if you are not familiar with the concept).
Newton's Law of Cooling says that the temperature of an object changes at a rate proportional to the difference between its own temperature and the temperature of its surroundings. As an equation, dT/dt = -k(T - Ta), where Ta is the ambient temperature and k is a positive constant. The minus sign does the physical work. A body hotter than its surroundings has T - Ta > 0, so its temperature falls, and a colder body warms up. All three examples below start from this one line and add a heat source or more rooms to it.
Cooling with No Temperature input
This example can be the most simplest case of Cooling problem and it would show you the essense of Newton's Law of cooling. The situation can be illustrated as shown below. Let's assume that you have a hot drink (like hot coffee) and put it on the table and put a thermometer in it and let it alone for several hours. You would know (from experience) that the temperature will gradually decrease. This example would explain how the temperature would change.
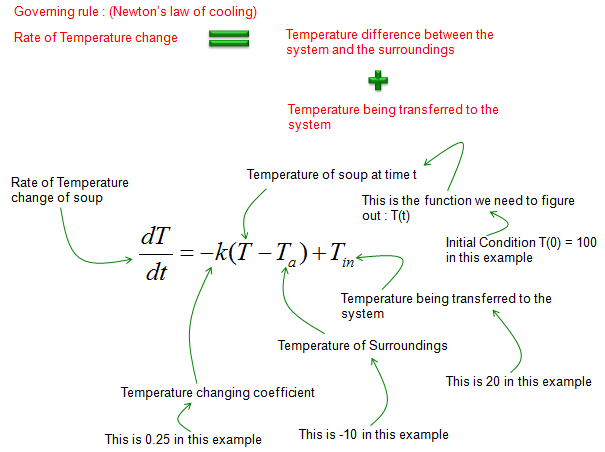
The governing equation for this case can be illustrated as below. Try to follow each and every parts including all the arrows in this illustration and comments, and you would automatically get a differential equation for the situation.
If you just convert the governing law shown above into a matehmatical form, you would get the differential equation as shown below.
Let's solve this equation. With the new variable u = T + 10, the equation becomes du/dt = -0.25u, so u decays exponentially. The initial condition T(0) = 100 gives u(0) = 110, and the solution is T(t) = -10 + 110 e-0.25t. The soup approaches the ambient temperature of -10 degrees C but never goes below it. The time constant is 1/k = 4 time units. After each ln(2)/k, about 2.77 time units, the gap between the soup and the surroundings is halved. The page does not state the time unit, so it is whatever unit k is measured in, for example hours if k = 0.25 per hour.
The whole cooling curve is one exponential : T(t) = Ta + (T(0) - Ta) e-kt. Only the gap to the ambient temperature decays, and the ambient temperature is the final value.k sets the speed, not the end point : A larger k cools the soup faster, but it still ends at Ta. The time constant 1/k is the time the gap needs to shrink to about 37 percent.The equation is linear and first order : One initial value, T(0), is enough to fix the solution.
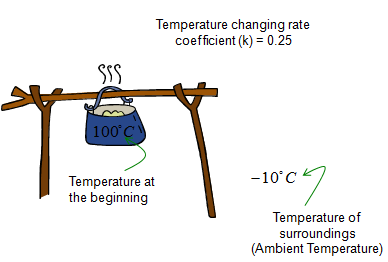
Cooling with Temperature input
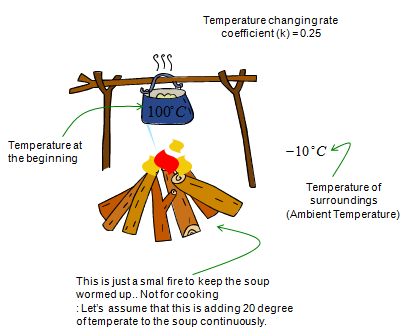
This example is just a little extension to previous example. In this situation, a simple heat source is added. So you would have two factors influencing on the system. One factor is removing heat (cooling) and the other factor is adding heat (heating). The situation can be illustrated as shown below.
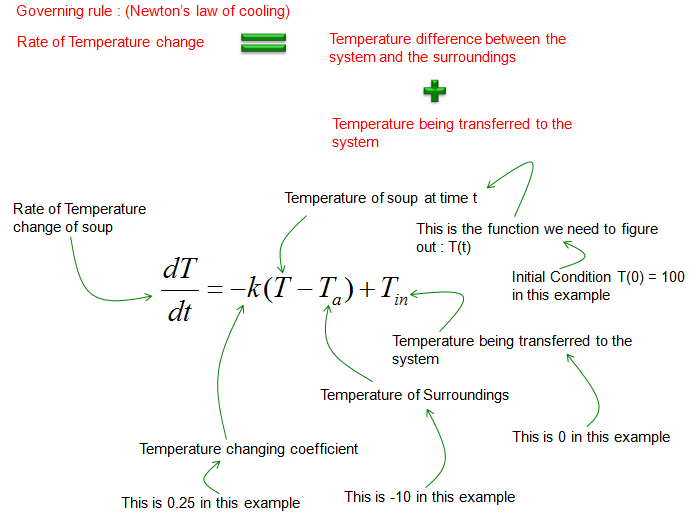
The governing equation for this case can be illustrated as below. Try to follow each and every parts including all the arrows in this illustration and comments, and you would automatically get a differential equation for the situation.
If you just convert the governing law shown above into a matehmatical form, you would get the differential equation as shown below.
The heat source changes where the temperature settles, not how fast it gets there. At the final temperature dT/dt = 0, so -0.25(T + 10) + 20 = 0 and T = 70 degrees C. The solution is T(t) = 70 + 30 e-0.25t. The soup cools from 100 toward 70 degrees C with the same time constant of 4 time units, because k has not changed. Note one detail about units. Tin is a heating rate, measured in degrees per unit time, even though the diagram calls it a temperature. That is why it adds directly to dT/dt.
A constant heat input shifts the final temperature : The final value becomes Ta + Tin/k. Here that is -10 + 20/0.25 = 70 degrees C.The decay rate is unchanged : The heater does not appear in the homogeneous part of the equation, so the exponential still has the rate k.The initial value decides the direction : Soup that starts above 70 degrees C cools down to it, and soup that starts below 70 degrees C warms up to it.
Home Heating
This example would show you a more realistic case but would look much more complicated than the examples shown above. However, don't get scared of it just by the complexity. However complicated a situation look, you can always break the situation into several component which is simple enough for you to attack. Once you get the several simple blocks, just figure out the governing equation for each of the simple block and figure out the differential equation for it.
When you complete building the differential equation for all the simpler component blocks, you can simply put all those equations together and get a complete system equation.
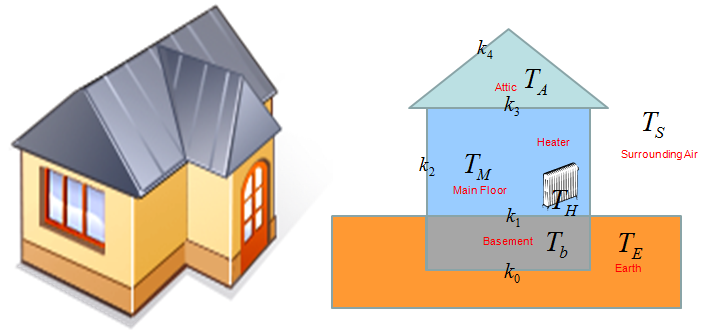
The situatioin we have to solve is to deduce the mathematical model to represent the temperature over time inside a house. It can be illustrated as shown below. This house is made up of several sectors - Basement, Main Floor,Attic and Surrounding Air. Each of these components has a couple of boundaries with the other components and each of the boundary has different heat tranfer rate.
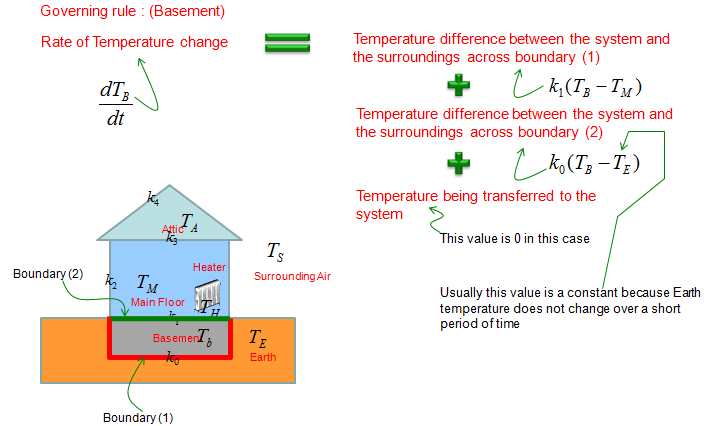
First, let's deduce the differential equation for the basement. It can be illustrated as shown below. Try to follow each and every parts including all the arrows in this illustration and comments, and you would automatically get a differential equation for the situation.
If you combine all the factors described in the illustration into an equation, you would get a differential equation as shown below.
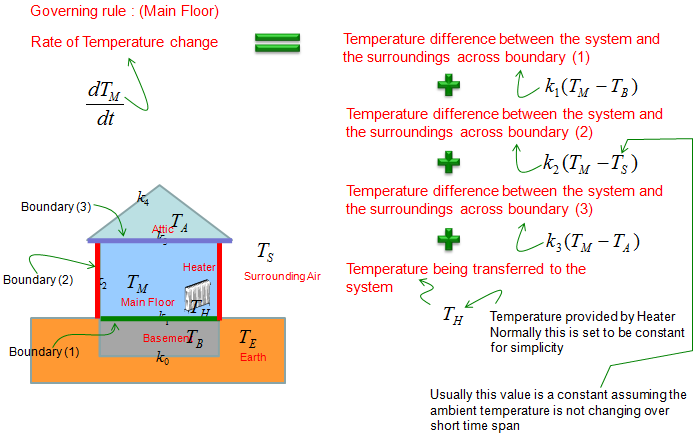
Next, let's deduce the differential equation for the Main Floor. It can be illustrated as shown below. Try to follow each and every parts including all the arrows in this illustration and comments, and you would automatically get a differential equation for the situation.
If you combine all the factors described in the illustration into an equation, you would get a differential equation as shown below.
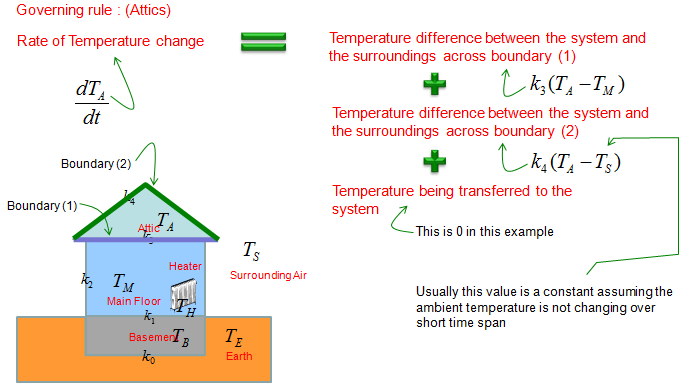
First, let's deduce the differential equation for the Attic. It can be illustrated as shown below. Try to follow each and every parts including all the arrows in this illustration and comments, and you would automatically get a differential equation for the situation.
If you combine all the factors described in the illustration into an equation, you would get a differential equation as shown below.
Now if you just put together all the individual equations for each individual component, you would get a system equation (simultaneous equation) as shown below.
Before you use this system, check two details against the single room examples. The first detail is the sign. Newton's Law of Cooling has a minus sign, dT/dt = -k(T - Ta), but the equations above write +k0(TB - TE) and so on. With positive k, that sign makes a warm basement heat up even faster, and every temperature grows without limit. The correct form is dTB/dt = -k0(TB - TE) - k1(TB - TM), and the same minus sign applies to every k term of the main floor and of the attic. The heater term +TH keeps its plus sign.
The second detail is the attic equation. It uses k2 for the boundary between the attic and the main floor. But the attic diagram and the main floor equation both use k3 for that boundary, and k2 belongs to the main floor walls. So the attic equation should read dTA/dt = -k3(TA - TM) - k4(TA - TS).
With both corrections, the system is linear, dT/dt = AT + b, with T = [TB, TM, TA]T. The matrix is A = [[-(k0 + k1), k1, 0], [k1, -(k1 + k2 + k3), k3], [0, k3, -(k3 + k4)]], and the input vector is b = [k0TE, k2TS + TH, k4TS]T. For positive k values, A is symmetric and all its eigenvalues are negative. So every room settles at the steady state T = -A-1b, whatever temperatures the rooms start from.
Each room is one first-order equation : A house with three rooms gives three coupled equations, and each boundary adds one k term to the two rooms it separates.Every heat loss term carries a minus sign : The term -k(T - Tneighbor) pulls a room toward its neighbor. A plus sign there describes a system that runs away.The coupling matrix is symmetric : The boundary k1 appears in both the basement and the main floor equations with the same value, and so does k3 for the attic.Constant outside temperatures act as inputs : TE, TS and the heater TH go into the vector b, and they set the final room temperatures.