|
Engineering Math - Differential Equation |
||
|
Physiologically Based Pharmacokinetic Model (Oxytetracycline Residues in Sheep)
This is a typical real life problem that can be extended from the mixing problems (tank problems) that we saw in previous examples.
This example came from the following reference. If you want to get further details, refer to following source.
J. vet. Pharmacol. Therap. 26, 55–63, 2003.
A physiologically based pharmacokinetic model for oxytetracycline residues in sheep
A. L. CRAIGMILL Food Animal Residue Avoidance Databank, Environmental Toxicology Extension, University of California, Davis, CA 95616,USA
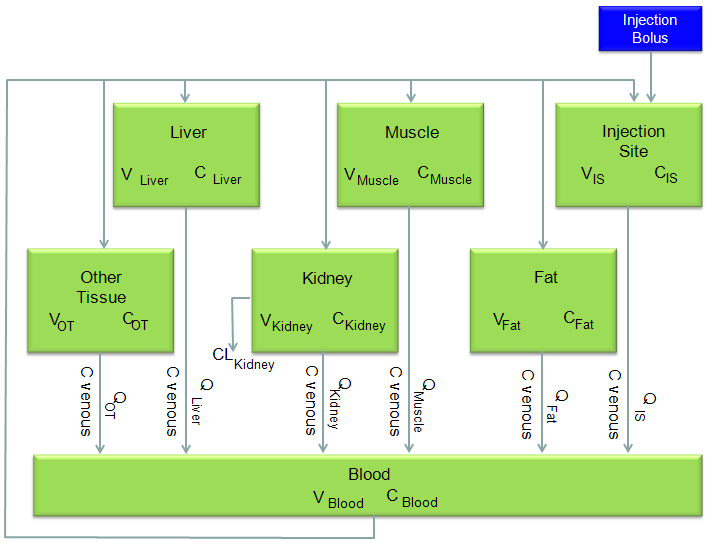
This is to model to see how a chemical injected into a body of an animal spread into all the organs and how the concentration of the chemical changes over time in each organs. The diagram for the model is shown below. It would look complicated... it is. But this is real life problem and most of real life problems are much more complicated than the one you see in the textbook. But point is that even such a complicated model like this are based on the same logic that you learned from the text book. Of course it is not easy to recognize the direct relationship between the real life problem and the text book examples. However, don't get disappointed if you don't recognize the relationship within 5 mins or even within a couple of hours. For the realife problem like this, it would take a least several months just to understand the details and reach the point where you can draw mathematical formula. So very important characteristics that you should have in addition to mathematical skills is to have 'persistence', 'perseverance'.
Anyway... if you consider each organs of the following diagram to be a tank of mixing problem that we covered in previous examples, this model can be just a mixing problem with 7 tanks.
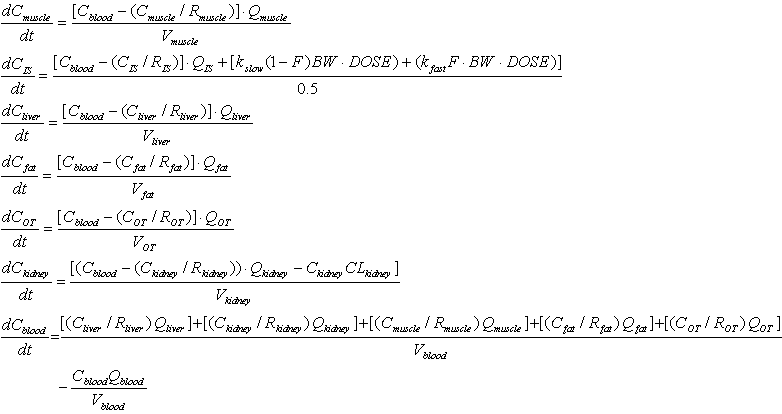
I would not want to describe each and every steps to draw out the differential equations from this model. I would just show the final outcome of the model from the reference. Just look at the equation and see if you can understand overal logics.
|
||