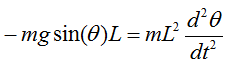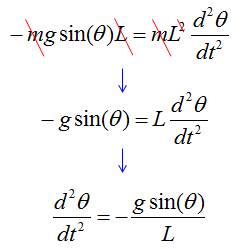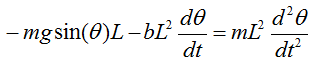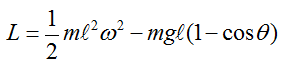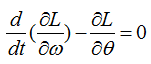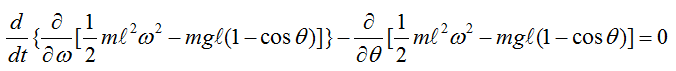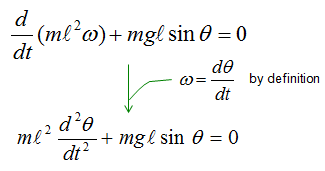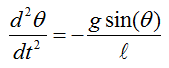|
Engineering Math - Differential Equation |
||
|
Simple Pendulum - Newtonian
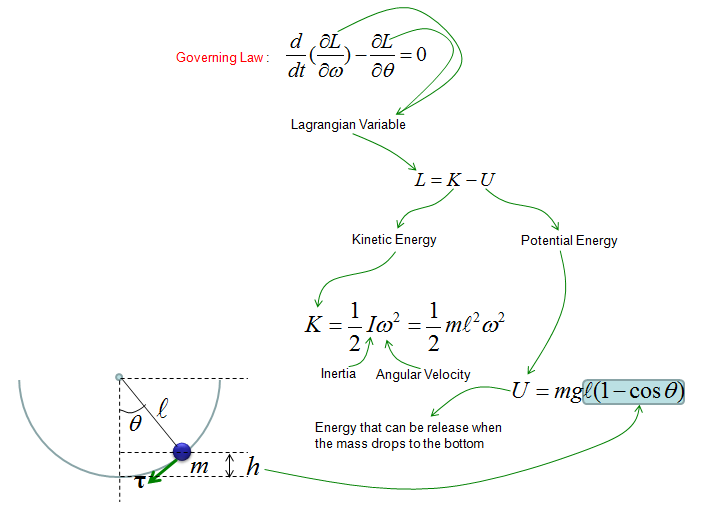
Now let's look at another famous example, 'Simple Pendulum (Single Pendulum)'. Governing Law is same as other dynamic system saying "Total Force being applied to a moving body represents the motion of the body". Basic format is derived from F = ma. The only difference is that Pendulum is for rotational motion whereas F=ma is for linear movement, but the basic concept is same.
NOTE : Before look into the derivation of the equation, it would be good to have some intuitive understandings on the solution of the differential equation for this model. Check out this page and see how the solution graph changes as the parameters in the equation changes.
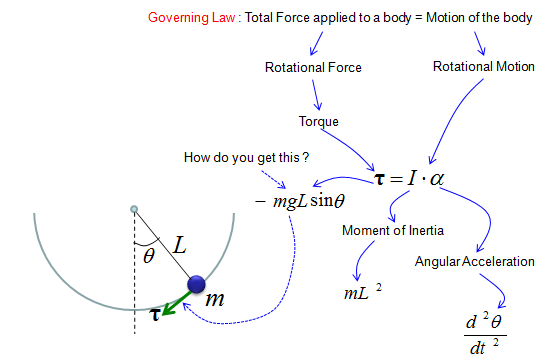
Following is each components of the government equation for the simple pendulum.
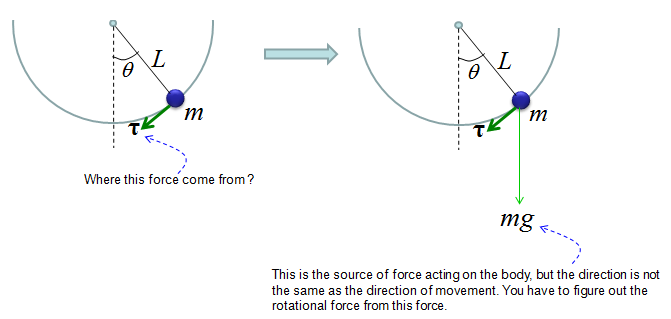
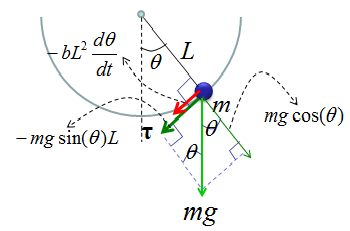
As shown above, the key factor in the governing equation is Torque and you may ask "Where does this Torque come from ?". In another word, what is the source of the torque. The source of the torque comes from the gravity from the Earth since we don't apply any additional force to the pendulum. You just lifted up the pendulum and just let it go. You didn't push the pendulum and just let it go. So the only source of the driving force is gravitational force. The gravitational force is applied in the direction as shown on the right side of illustration below.
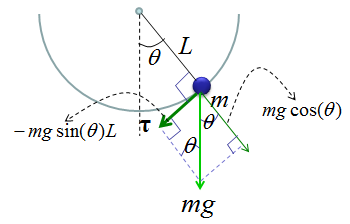
Then how can I derive the torque from the gravitational force ? If you just draw a couple of additional arrows as shown below, you would easily figure out the Torque from high school trigonometry.
With this understanding and the first illustration, you would get a differential equation as follows.
With a little bit of methematical touch, you would get much simpler equation as show below.
The equation shown above is the pendulum with no damping (e.g, no resistence by air and any other frictions). Now let's look at the case where the damping gets involved. You would the differential equation with damping just by adding an additional arrow show in red below.
If you just 'READ' the illustration shown above, you would get the following differential equation.
Solution :
Graphical solution for a simplified differential equation for this kind of undamped pendulum is in my visual note (www.slide4math.com) : solution 1, solution 2
|
||