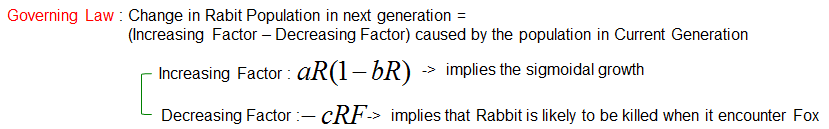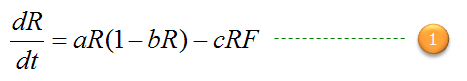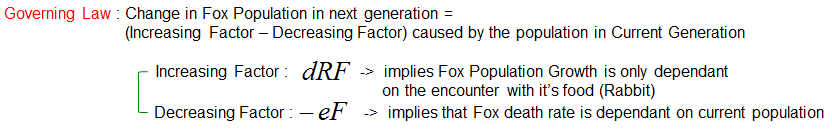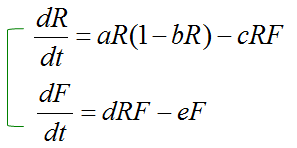|
Engineering Math - Differential Equation |
||
|
Prey and Predator Model
Let's start with an Intuitive approach. Let's assume that you are oberving a Rabit population and Fox population in an area. And by common sense and observation, you would know Fox hunts Rabits meaning Fox is the predator and Rabit is the prey in the area.
Without using any math and just using your intuition, think of what would happen if the number of Fox would increase in the area ? You may easily think that the number of Rabit will decrease because more and more rabbits will be killed by Fox. It is easy. Then, will all the rabit will be eaten by Fox and they will completely disappear ? The answer to this question is not easy. The answer can be 'Maybe Yes, Maybe No. The answer would depend on the population changes of Fox and how fast the fox eats away rabits etc. To get the answer to this kind of tricky question you need to use mathematical modeling and understand the exact relationship between the two populations.
Again only using your intuition, think of what will happen when the birth rate of Rabit increases and the number of Rabit increases ? You may easily guess that the number of Fox will increase as well because they get food more easily. Then, will this situation goes forever ? Will fox hunt rabit such easily forever ? Probably not, because as fox hunt rabit more easily and the number of fox increases, at some point the number of rabit may decrease since too many rabits are hunted. Decreasing number of rabbit means decreasing food for Fox and eventually the number of Fox will decrease as well.
Now you may roughly understand the inter-relationship between Rabbit population and Fox population. But if I ask you about exactly when the rabbit popuation would grow or shrink or exactly when the fox popuation would grow or shrink. You cannot answer this questions without exact mathematical modeling of those population changes.
In this section, we will derive very basic models of these population changes using differential equation.
First let's think of the rule (Governing Law) for the population change of the rabit. It can be described as follows.
Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the rabbit as follows.
Now let's think of the rule (Governing Law) for the population change of the fox. It can be described as follows.
Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the fox as follows.
Now you have a two equations for rabbit and fox population. However, you cannot solve the two equation separately because Rabbit population equation has fox population as a part of the equation and Fox population equation has rabbit population as a part of the equation.
To get the solution for the two equation, you have to combine the two into a system equation (simultaneous equation) as show below and solve the system equation. For now, don't worry about solving the proplem. If you just understand the meaning of this equation, my goal is done. I will give you a graphical solution for this equation later.
|
||