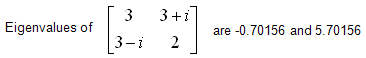Hermitian Matrix

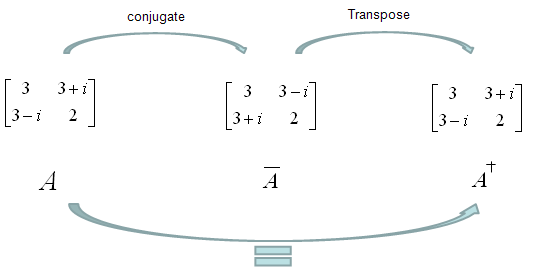
Hermitian Matrix is a special type of  matrix, which is same as its conjugate transpose as expressed below.

In orther words, a Hermitian Matrix has following properties

• The entries on the main diagonal are real.
• The element in the ith row and jth column is equal to the complex conjugate of the element in the jth row and ith column
• Eigenvalues of all Hermitian Matrix are all real

One example of Hermintian Matrix is as follows. In this example, if you conjugate the matrix A and then transpose it, the result is same as the original matrix (A). So you can say the matrix 'A' is a Hermitian matrix.

One of the important characteristics of Hermitian Matrix is that Eigenvalues of all Hermitian Matrix are all real as shown in the following example.

Related Reading : Hermitian Conjugate, Conjugate Transpose