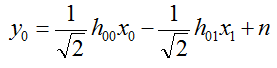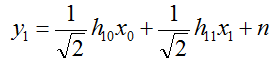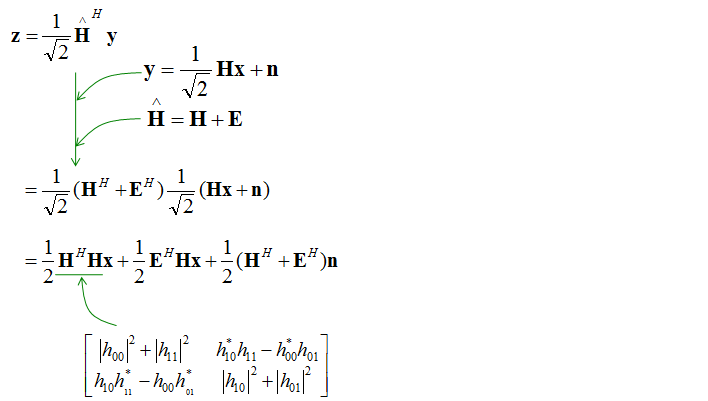4G/LTE - Diversity

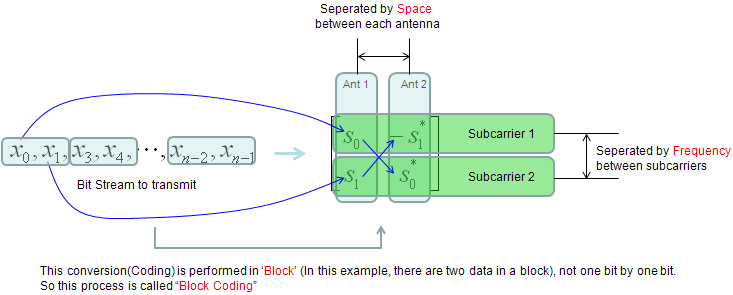
SFBC (Space Frequency Block Coding)

SFBC is a kind of coding scheme for TX diversity and I hope you can figure out the meaning of SFBC directly from following illustration. Just connect the words in red -:). Regarding the mapping from Bit Stream (represented in x and symbol sequence represented in s, I am assuming BPSK case)

Following is the SFBC for 4 Antenna case which is simple extension of 2 antenna case as shown above. Regarding the mapping from Bit Stream (represented in x and symbol sequence represented in s, I am assuming BPSK case)

Analysis for SFBC

Now let's try to go through formal analysis technique (mathematical analysis) for SFBC. If you are not strongly interested, just skip this part before you get bored. Even if you are strongly interested, don't expect to understand all of this just from the first reading if you are new to this kind of analysis. It would take several month to get familiar with these. It is not because mathematical part is so tough.. but because it would be tricky to interpret the meaning of those mathematical forms and correlate them to physical entities. (If you have high school math and basic linear algebra in university, you would be good enough in terms of mathematical skills for this).

Mathematical framework for this section came from Performance of Space-Frequency Block Codes in 3GPP Long Term Evolution by Liang Heng and illustration/descriptions are mine.

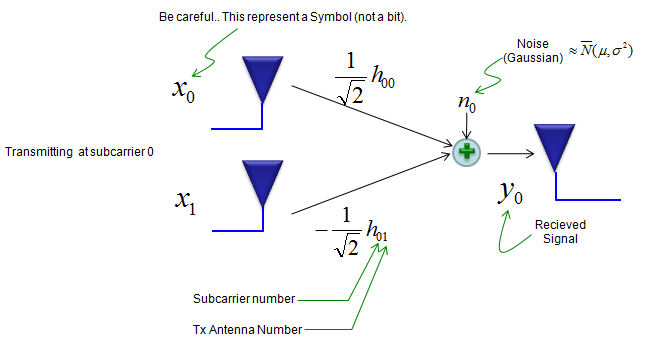
For simplicity, let's look into the case with two transmitter antenna and one reciever antenna to perform the transmission in diversity. It can be illustrated as shown below.

Now let's suppose channel coefficient of each diversity path is shown as below and two symbols x0,x1 is being transmitted at the sub carrier 0. (Take care of the index number attached to each channel coefficient h.)

We can represent the received signal y0 as shown below. If you can convert this equation in your mind into an illustration as above, it mean you would have good understanding of the meaning of the equation. This kind of mental conversion practice is important because it would help a lot when you read formal paper or thesis on this field.

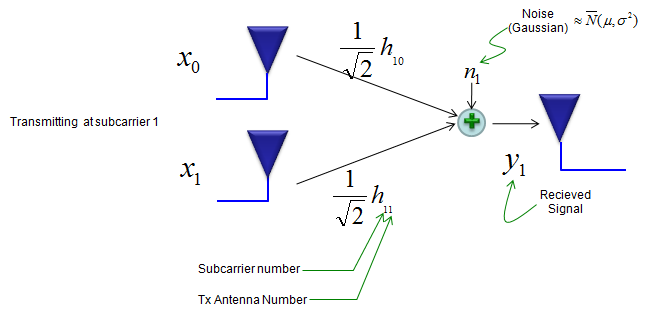
Now let's suppose channel coefficient of each diversity path is shown as below and two symbols x0,x1 is being transmitted at the sub carrier 1. (Take care of the index number attached to each channel coefficient h.)

We can represent the received signal y1 as shown below.

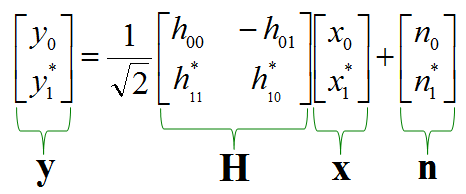
Now you have two equations representing y0, y1. You can combine the two equations into one matrix equation as shown below. If you are not familiar with this combining process, go through the basic linear algebra course.

You can simplifiy this matrix equation as follows if you replace each of the vector and matrix with vector/matrix symbols. A lot of papers and text book would just start with this kind of equations. So it would be extremly difficult for you to understand the meaning of the equation if you are not familiar with all the conversion steps we went through above.

Since we don't know real values in the channel matrix, we have to estimate (calculate by an algorithm) the channel matrix. The estimated matrix can be represented as shown below.

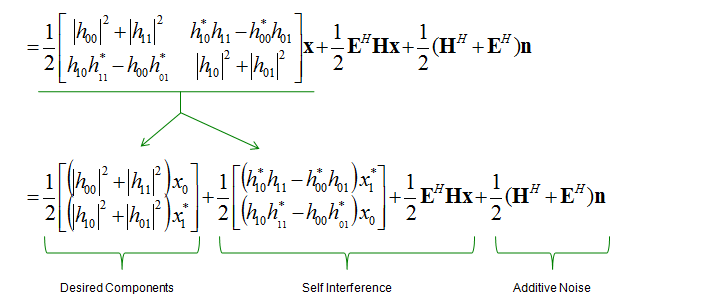
With these matrix, you can figure out the desired signal by a special technique called maximum likelyhood decoding as shown below. Questions is how we get the first equation.. this would require at least several month of investigation (I will try to get back to this later). For now, just take this as given.