4G/LTE - PHY Channel

  

 

 

 

SSS (Secondary Synchronization Channel)

 

SSS is a specific physical layer signal that is used for radio frame synchronization. It has characterstics as listed below.

  • Mapped to 72 active sub carriers(6 resource blocks), centered around the DC subcarrier in slot 0 (Subframe 0) and slot 10 (Subframe 5) in FDD.
    • The sequence of SSS in subframe 0 and the one in subframe 5 are different from each other
  • Made up of 62 Scrambling Sequence (based on m-sequence)
    • The value in odd indexed resource element and the one in even indexed resource elements is generated by different equation
  • Used for Downlink Frame Synchronization
  • One of the critical factors determining Physical Cell ID

May Not be a big issues for most of the case since it would be working fine for most of the device that you have for test. Otherwise it would have not been given to you for test.

However, If you are a developer working at early stage of LTE chipset, this would be one of the first signal you have to implement.

 

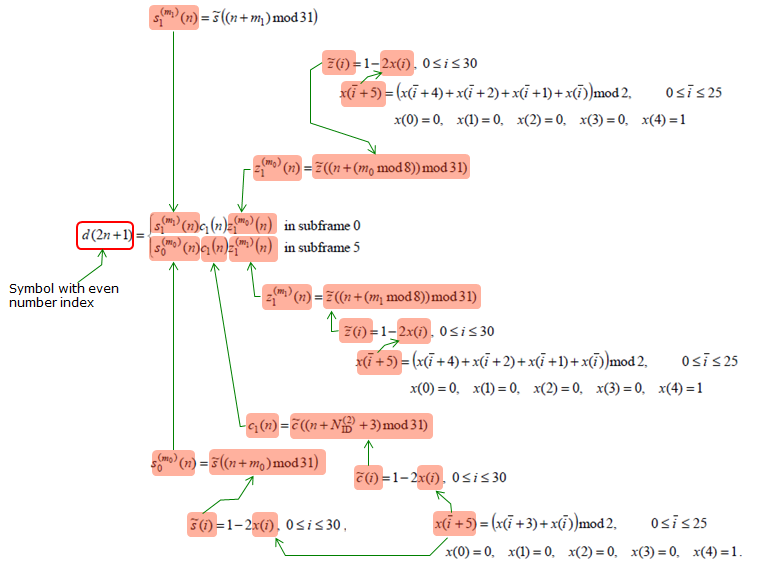
The exact PSS symbol calculation is done by the following formula as described in 36.211 - 6.11.2. For the specific example of generated PSS, refer to Matlab : Toolbox : LTE : SSS page.

 

 

 

Symbol Generation of SSS

 

 

 

< Resource Element Mapping >

 

 

 

< Matlab code for SSS Generation >

 

Following is the Matlab code for SSS Generation. This is only for the SSS in subframe 0 and I think you can easily modify this to generate the sequence for subframe 5.

    clear all;

     

    NID1 = 0;

    NID2 = 0;

    q_prime = floor(NID1/30);

    q = floor(((NID1+q_prime*(q_prime+1)/2))/30);

    m_prime = NID1 + q *(q+1)/2;

    m0 = mod(m_prime, 31);

    m1 = mod(m0 + floor(m_prime/31)+1,31);

     

    %%%%%%%%%%%%%%%%% generate d_even() sequence %%%%%%%%%%%%%%%%

    % Generate the sequence x_s() : x() for calculating s_tilda()

    x_s = zeros(1,31);

    x_s(1:5) = [0 0 0 0 1];

     

    for i = 0:25

        x_s((i+5)+1) = mod(x_s(i+2+1)+x_s(i+1),2);

    end;

     

    % Generate the sequence x_c() : x() for calculating c_tilda()

    x_c = zeros(1,31);

    x_c(1:5) = [0 0 0 0 1];

     

    for i = 0:25

        x_c((i+5)+1) = mod(x_c(i+3+1)+x_c(i+1),2);

    end;

     

    % Generate the sequence s_tilda()

    s_tilda = zeros(1,31);

    for i = 0:30

        s_tilda(i+1) = 1 - 2*x_s(i+1);

    end;

     

    % Generate the sequence c_tilda()

    c_tilda = zeros(1,31);

    for i = 0:30

        c_tilda(i+1) = 1 - 2*x_c(i+1);

    end;

     

    % Generate s0_m0_even()

    s0_m0_even = zeros(1,31);

    for n = 0:30

        s0_m0_even(n+1) = s_tilda(mod(n+m0,31)+1);

    end;

     

    % Generate c0_even()

    c0_even = zeros(1,31);

    for n = 0:30

        c0_even(n+1) = c_tilda(mod(n+NID2,31)+1);

    end;

     

    % Calculate d_even_sub0

    d_even_sub0 = s0_m0_even .* c0_even;

     

    %%%%%%%%%%%%%%%%% generate d_odd() sequence %%%%%%%%%%%%%%%%

    % Generate the sequence x_s() : x() for calculating s_tilda()

    x_z = zeros(1,31);

    x_z(1:5) = [0 0 0 0 1];

     

    for i = 0:25

        x_z((i+5)+1) = mod(x_z(i+4+1) + x_z(i+2+1) + x_z(i+1+1)+ x_z(i+1),2);

    end;

     

    % Generate the sequence z_tilda()

    z_tilda = zeros(1,31);

    for i = 0:30

        z_tilda(i+1) = 1 - 2*x_z(i+1);

    end;

     

    % Generate s1_m1_odd()

    s1_m1_odd = zeros(1,31);

    for n = 0:30

        s1_m1_odd(n+1) = s_tilda(mod(n+m1,31)+1);

    end;

     

    % Generate c1_odd()

    c1_odd = zeros(1,31);

    for n = 0:30

        c1_odd(n+1) = c_tilda(mod(n+NID2+3,31)+1);

    end;

     

    % Generate z1_m0_odd()

    z1_m0_odd = zeros(1,31);

    for n = 0:30

        z1_m0_odd(n+1) = z_tilda(mod(n+mod(m0,8),31)+1);

    end;

     

    % Calculate d_odd_sub0

    d_odd_sub0 = s1_m1_odd .* c1_odd .* z1_m0_odd;

     

    % Calculate d_sub0

    d_sub0 = zeros(1,62);

    d_sub0(1:2:end-1) = d_even_sub0;

    d_sub0(2:2:end) = d_odd_sub0;

     

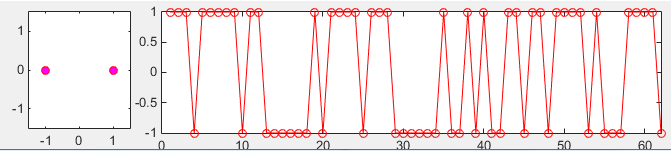
    subplot(1,5,1);

    plot(real(d_sub0),imag(d_sub0),'ro','MarkerFaceColor',[1 0 1]);axis([-1.5 1.5 -1.5 1.5]);

    subplot(1,5,[2 5]);

    plot(real(d_sub0),'ro-');xlim([0 length(d_sub0)]);

     

 

    Following is numberical output of d_sub0

     

    1  1  1  -1  1  1  1  1  1  -1  1  1  -1  -1  -1  -1  

    -1  -1  1  -1  1  1  1  1  -1  1  1  1  -1  -1  -1  -1  

    -1  -1  1  -1  -1  1  -1  1  -1  -1  1  1  -1  1  1  -1  

    1  1  1  1  -1  1  -1  -1  -1  1  1  1  1  -1

     

 

 

< Python Code for SSS generation >

 

Following is the Python code to generate SSS. It generate two sequences with given NID1 and NID2, one for subframe 0 and the other one for subframe 5.

NOTE : The sequence generated by this code is tested to work with SSS detection from I/Q captured from eNB Simulator (Amarisoft Callbox)

    def generate_sss(NID1,NID2):

     

        q_prime = np.floor(NID1/30)

        q = np.floor(((NID1+q_prime*(q_prime+1)/2))/30)

        m_prime = NID1 + q *(q+1)/2

        m0 = m_prime % 31

        m1 = (m0 + np.floor(m_prime/31) + 1) % 31

     

        # generate d_even() sequence

        x_s = np.zeros(31)

        x_s[:5] = [0, 0, 0, 0, 1]

        for i in range(26):

            x_s[i+5] = (x_s[i+2] + x_s[i]) % 2

     

        x_c = np.zeros(31)

        x_c[:5] = [0, 0, 0, 0, 1]

        for i in range(26):

            x_c[i+5] = (x_c[i+3] + x_c[i]) % 2

     

        s_tilda = 1 - 2*x_s

        c_tilda = 1 - 2*x_c

        s0_m0_even = np.zeros(31)

        s1_m1_even = np.zeros(31)

        for n in range(31):

            s0_m0_even[n] = s_tilda[int((n+m0)%31)]

            s1_m1_even[n] = s_tilda[int((n+m1)%31)]

     

        c0_even = np.zeros(31)

        for n in range(31):

            c0_even[n] = c_tilda[int((n+NID2)%31)]

     

        d_even_sub0 = s0_m0_even * c0_even

        d_even_sub5 = s1_m1_even * c0_even

     

        # generate d_odd() sequence

        x_z = np.zeros(31)

        x_z[:5] = [0, 0, 0, 0, 1]

        for i in range(26):

            x_z[i+5] = (x_z[i+4] + x_z[i+2] + x_z[i+1] + x_z[i]) % 2

     

        z_tilda = 1 - 2*x_z

        s1_m1_odd = np.zeros(31)

        s0_m0_odd = np.zeros(31)

        for n in range(31):

            s1_m1_odd[n] = s_tilda[int((n+m1)%31)]

            s0_m0_odd[n] = s_tilda[int((n+m0)%31)]

     

        c1_odd = np.zeros(31)

        for n in range(31):

            c1_odd[n] = c_tilda[int((n+NID2+3)%31)]

     

        z1_m0_odd = np.zeros(31)

        z1_m1_odd = np.zeros(31)

        for n in range(31):

            z1_m0_odd[n] = z_tilda[int((n+m0%8)%31)]

            z1_m1_odd[n] = z_tilda[int((n+m1%8)%31)]

     

        d_odd_sub0 = s1_m1_odd * c1_odd * z1_m0_odd

        d_odd_sub5 = s0_m0_odd * c1_odd * z1_m1_odd

     

        # calculate d_sub0

        d_sub0 = np.zeros(62)

        d_sub0[::2] = d_even_sub0

        d_sub0[1::2] = d_odd_sub0

        sss0 = d_sub0

     

        d_sub5 = np.zeros(62)

        d_sub5[::2] = d_even_sub5

        d_sub5[1::2] = d_odd_sub5

        sss5 = d_sub5

     

        return sss0, sss5

     

 

 

 

SSS Detection Algorithm

 

The SSS detection algorithm can be illustrated as below. As shown here, you need to an accurate result of PSS detection and frequency error estimation which is explained in this note.

 

 

 

 

Reference :

 

[1] Synchronization and Cell Search