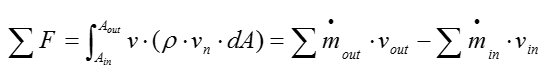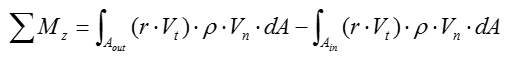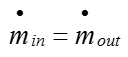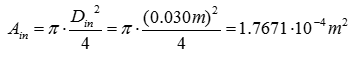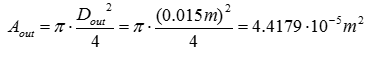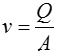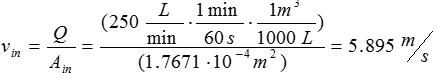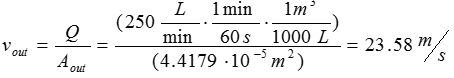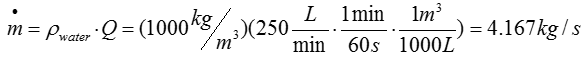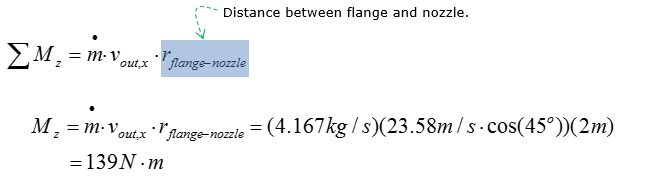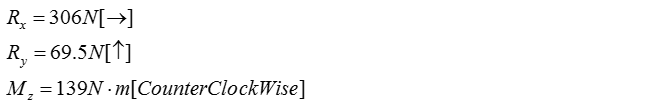Mechanical Engineering

  

 

 

 

Fluid Mechanics : Linear and Angular Momentum

 

Linear and angular momentum equations are used to calculate the reaction forces and moments exerted by the control volume to maintain static equilibrium under applied forces and/or moments by the working fluid(s)

 

In engineering and real-life, examples of linear and angular momentum equation application include:

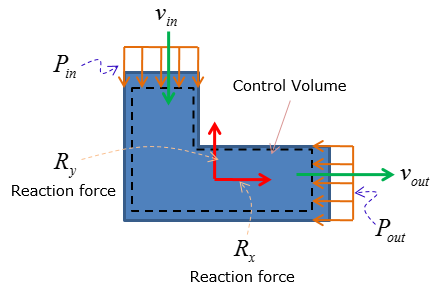
  • Calculating the reaction moment on a rotating jet hose that feeds water to grass to maintain constant speed of rotation
  • Analyzing the reaction forces and moments supplied by screws that support fluid-powered systems, such as a jet engine on an airplane

 

 

Linear momentum equation

 

The linear momentum equation is used to calculate the reaction forces on a control volume to maintain static equilibrium

 

 

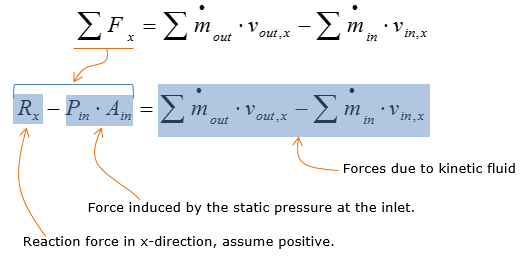
The equation is initially stated (in general)as following for steady-state condition:

Meaning of some important terms in this equation is as follows :

 

The equation above states that sum of the forces are equal to the difference between mass flow rate times velocity parallel to the force at the outlet and inlet of the control volume

Static pressure of the working fluid at the inlet and outlet are also elements of forces on the control volume, affecting the magnitude of reaction forces: static pressure always acts into the control volume

 

 

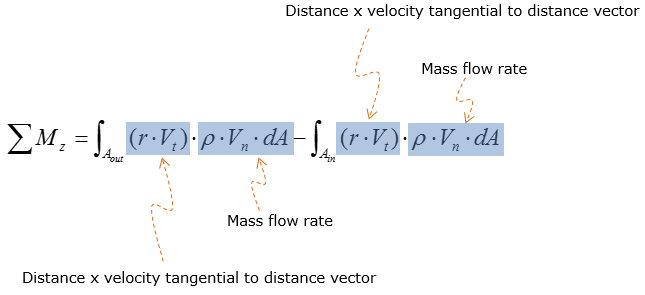
Angular momentum equation

 

The angular momentum equation is used to calculate the reaction moment on the control volume. Unlike the linear momentum equation, the static pressure at the inlet and outlet of the control volume does not affect the magnitude of the reaction moment. To calculate reaction moment, one must compute the distance between the inlet/outlet of the control volume and the location of the support system. For fluid-powered systems, screws are the most typical hardware used as support system that induce reaction forces and moments.

 

 

Meaning of some important terms in this equation is as follows :

 

 

 

Example 1 >

 

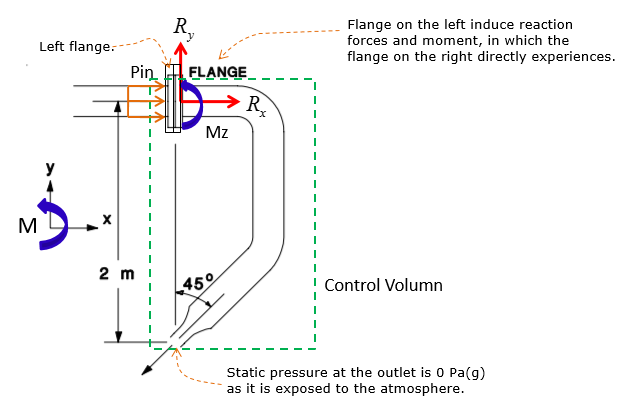
Water flows through the pipe shown at a rate of 250 litres/minute. It discharges to atmosphere at the nozzle outlet. The pipe has an inside diameter of 30 mm and the nozzle an inside diameter of 15 mm. The water pressure at the flange is 300 kPa(g). Determine the forces and moments the left flange exerts on the right flange. The pipe lies in the horizontal plane. Neglect the weight of the pipe itself and the water inside it.

 

 

Step 1: List the assumptions

  • Assume 1D flow where the velocity varies in one direction. This means no integral is required
  • The system is at steady-state where no accumulation is occurring in the control volume:
  • mass flow rate at the inlet and outlet are equal as expressed below

  • Water is incompressible: density of water is constant. Then the volumetric flow rate of water is also equal at the inlet and outlet of control volume. 

 

Step 2: Analyze the inlet and outlet properties

    As the cross-sectional area of the inlet and outlet are required to calculate the reaction forces, start off by calculating the cross-sectional area at the inlet and outlet of the control volume:

    Apply the given volumetric flow rate and the calculated cross-sectional areas to calculate the velocity of water at the inlet and outlet:

    Rearrange the volumetric flow rate equation above for v

    Use the velocity expression above to calculate the inlet and outlet velocities of water. Convert the given volumetric flow rate to m^3/s to compute for velocities in m/s. Recall that volumetric flow rate is equal at the inlet and outlet as the flow is assumed to be steady-state and water is incompressible.

       

    Calculate the mass flow rate through the system. Recall that the mass flow rate at the inlet and outlet of the control volume are equal based on steady-state assumption.

 

Step 3: Calculate the reaction forces

    Now that the velocity and cross-sectional area at the inlet and outlet are computed, linear momentum equation is now ready to be used to calculate the reaction forces induced by the flange, both in the x and y direction.

     

    Consider the reaction force analysis in the x-direction. Let Rx be the reaction force in the x-direction

     

    Expand and simplify the expression of forces due to kinetic fluid. This step is used to prepare the equation for plug and chug analysis.

     

     

    Consider the reaction force analysis in the y-direction. Let Ry be the reaction force in the y-direction.

     

    Reaction force in y-direction, assume positive. Since the outlet is at atmospheric pressure, there is no static pressure that creates force into the control volume.

     

    Expand on the linear momentum equation for Ry and then calculate Ry.

 

Step 4: calculate the reaction moment

    Since the flange is right beside the inlet, the forces on the inlet does not induce a rotational moment on the control volume. However, the outlet of the control volume is located 2m below the inlet, inducing a rotational moment since there is water flowing out of the nozzle (outlet in this case). The nozzle is oriented 45 degrees below horizontal, which indicates that only the horizontal component of the water velocity induces the force that creates the rotational moment about the flange.

    Then the reaction moment generated by the flange is calculated by multiplying the force and the vertical distance from the  flange.

     

 

Now let's summarize all the result we got. The magnitude of reaction forces and moment are stated below.