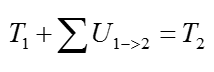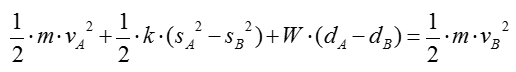|
Mechanical Engineering |
|||||||||||||
|
Conservation of Work and Energy
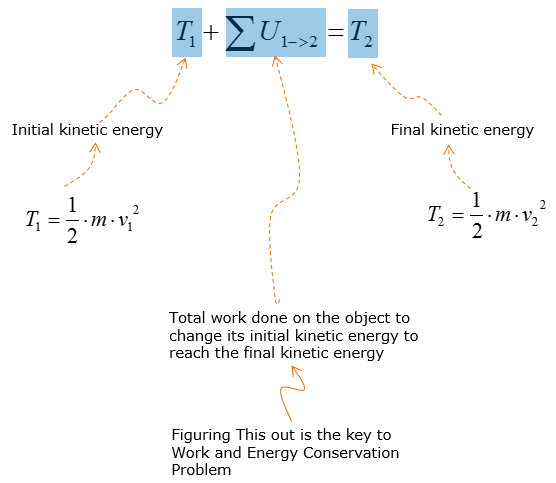
Conservation of Work and Energy equation is used to analyze the change in velocity of an object in motion based on its displacement due to applied force(s). The conservation equation is almost always preferred over kinematic equations as the magnitude of acceleration is not required to calculate initial or final velocity of an object. This is also known as principle of work and energy and this can be represented in equation as follows.
What does this mean ? What should I do to solve this equation ? A little bit expansion of the equation as follows would help you to understand overall meaning of the equation/
The equation above explains that the velocity of an object at state 2 is affected by the total applied work onto the object at state 1. Total work on/against the object can be done by weight, spring, couple moment, applied force, friction, etc.
What can we apply this for ? / Why we need to know about this ?
There are many fields you can apply this technique for, but followings are a couple of typical application of this technique.
Roller-coaster design:
Rocket design:
Example 1 >
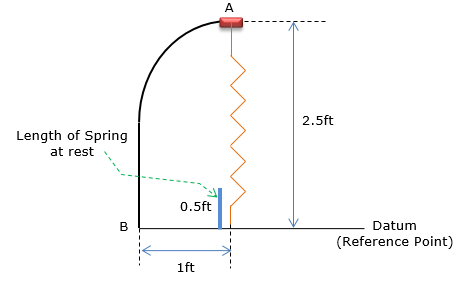
The 5-lb collar is released from rest at A and travels along the frictionless guide. Determine the speed of the collar when it strikes the stop B. The overall picture of the mode is illustrated as follows.
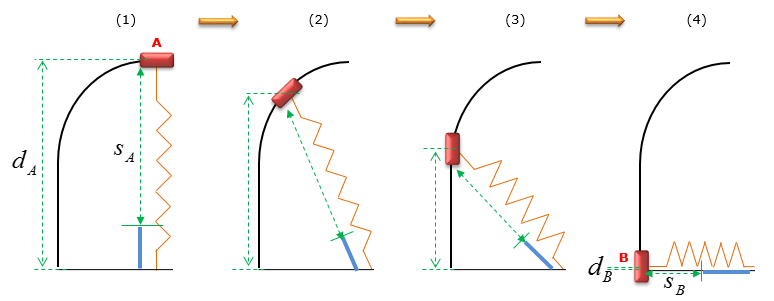
Just to give you some intuitive understandins on how the object moves in this model, I added some additional snapshots as follows.
Followings are the constants that are given :
Followings are the set of variables (parameters) that are given :
Spring does work ON the collar, since the resultant velocity is higher than the initial velocity.
The principle of work and energy is the governing equation as the initial and final length of the spring are the known quantities
The equation that describes this situation can be written as follows.
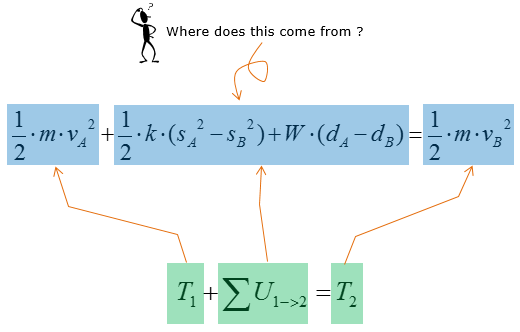
What does this mean ? How this equation is related to the standard equation explained at the beginning ? Following illustration would help you with this.
If we simplify this equation and rearrange the equation with reference to the velocity at point B, we can get an equation as shown below.
Now it is time to plug into all the specific numbers that are given to you in problem description and you would get the solution as follows.
|
|||||||||||||