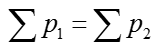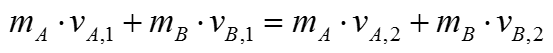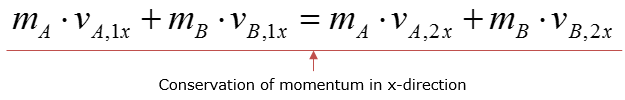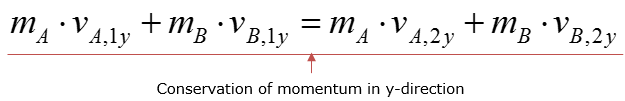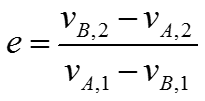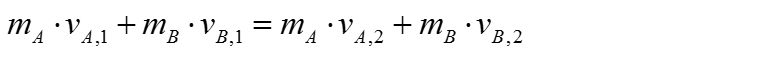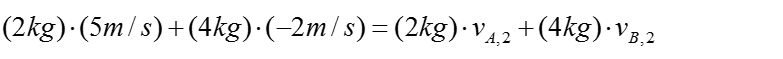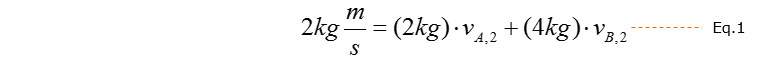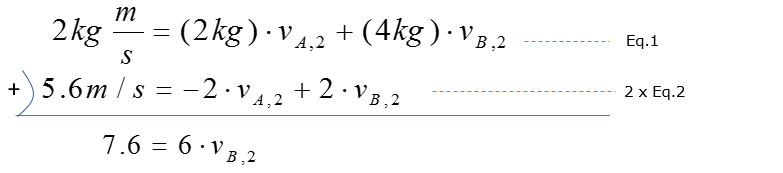Mechanical Engineering

Conservation of Momentum

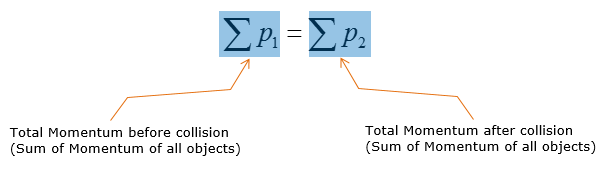
Conservation of momentum equation states that the momentum (represented as p) of two objects are conserved after collision. It can be represented as below in mathematical form.

The meaning of this simple equation is as follows and it is one of the most important physical properites in studying Dynamics.

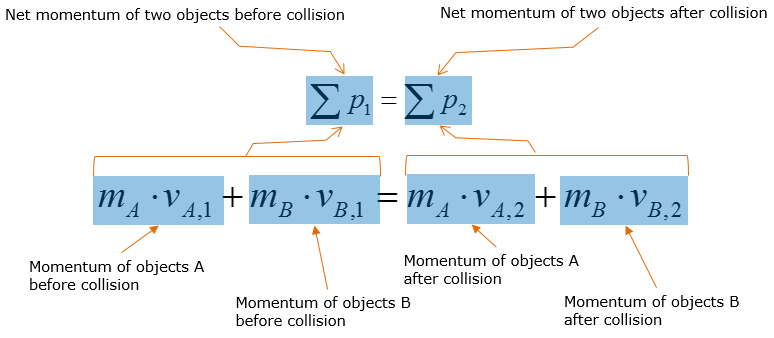
Getting a little bit further into this equation, let's assume that two objects be A and B collide against each other, then the expression above is expanded to

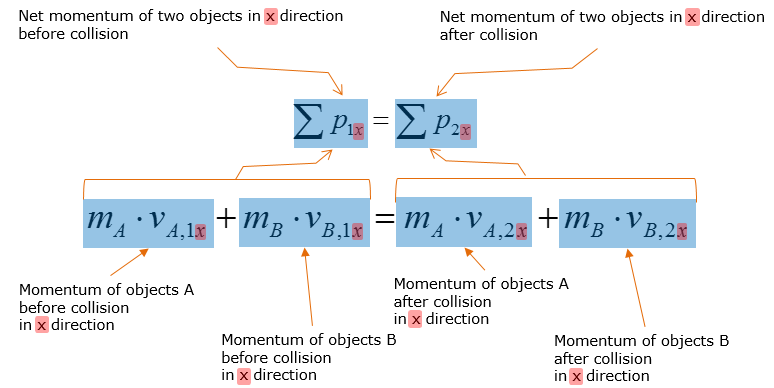
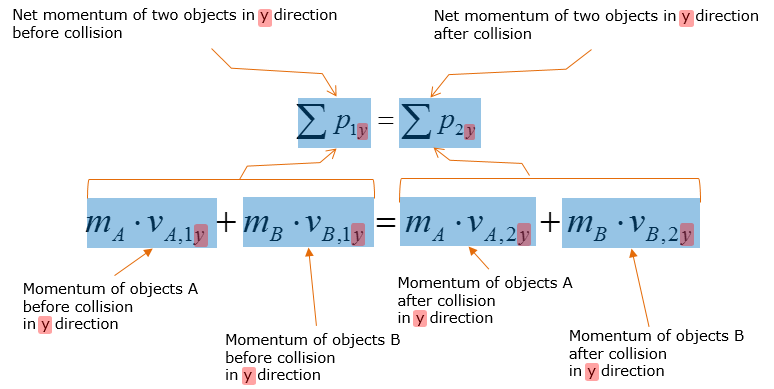
What does this mean ? How this equation is related to the original governing equation shown at the beginning of the page. It can be illustrated as follows.

The equation can only applied 1 dimensionally, meaning that if velocity of the objects have both x and y components before/after collision, the x and y components need to be analyzed separately

This kind of expansion (extending from 1 demension to 2 dimension) can be related to the original governing equation as follows :

Before solving problems with the conservation of momentum equation, there are other theories to learn. One of them is called 'Coefficient of Restitution' that is represented as follows :

The coefficient is used to represent the degree of kinetic energy loss in two objects after collision – the equation is applied for the momentum analysis across the line of impact

When e = 0: Plastic collision has occurred. Two objects are embedded after collision and move as one object.

        e = 1: Elastic collision. Both the momentum and kinetic energy are conserved after collision for both objects.

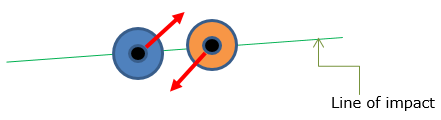
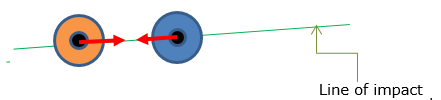
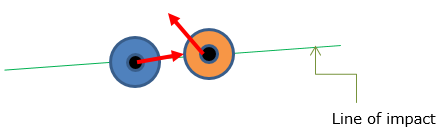
Types of Impact

When two object collide against each other, they hit (impact) in a few different mode as described below :

• Central impact: Center of mass (indicated as black dot) for the two bodies lie along the line of impact – velocity of objects have no effect on this type of impact

• Direct impact: The velocity of the two bodies are directed along the line of impact before collision

• Oblique impact: The velocity of one or two of the bodies is/are directed at an angle from the line of impact

What can we apply this for ? / Why we need to know about this ?

Collision analysis – velocity of object(s) before and after collision. One of the most practical concept in real-life situations(other than engineering) and laboratory research

Engineering Application(s):

• Calculating the velocity of the car after it rebounds from collision to analyze the efficiency of the bumper: Lower the velocity after rebounding, the more efficient the bumper
• Air hockey and pool are some of the most practical real-life applications to this concept

Example 1 >

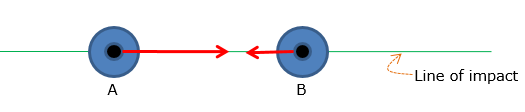
Disk A has a mass of 2 kg and is sliding forward on the smooth surface with a velocity of 5 m/s when it strikes the 4kg disk B, which is sliding towards A at 2 m/s, with direct central impact. If the coefficient of restitution between the disks is e = 0.4, compute the velocities of A and B just after collision.

Since collision is involved, conservation of momentum and coefficient of restitution are the governing equations to calculate the velocity of objects A and B after collision.

State the given parameters:

State the governing equations and put it into its simplest form after back-substituting the given parameters  – the two velocities will be solved by combining the two governing equations, Eq.1 and Eq.2:

If you were to solve the system of equations by hand, you can do the following:

-Solve for vB,2 first. -> Eq.1+2*Eq.2 to eliminate vA,2.

From this you get the final result as follows :

Back-substitute the value above into Eq.1 to solve for vA,2 -> vA,2 = -1.53m/s

Therefore the velocity of object A and B after collision is -1.53m/s and 1.27m/s, respectively

NOTE : Once you get the Eq1 and Eq2, you can get the solution with Matlab as follows :