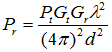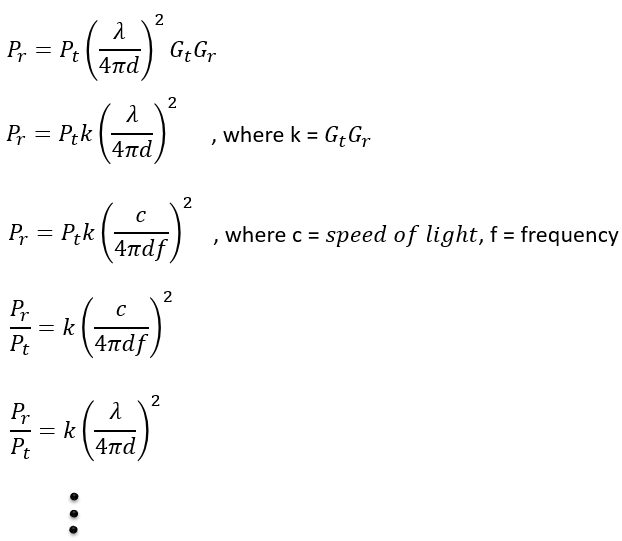|
RF |
||
|
Radio Range(Frris' Transmission Equation)
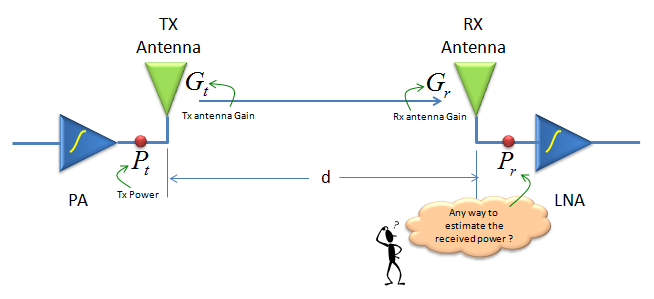
Frris' Transmission Equation is an equation that shows the relationship between the received power and various factors influencing the received power. To get a clearer understanding, let's think of a communication system that is made up of one transmitter RF front end and one reciever front end as illustrated below.
With all of these variables (factors), the received power (Pr) can be estimated by the equation shown below. This is Frris' Transmission Equation.
Following is the equation expressed in dB scale and that's why all the power and Gain parameters are combined by '+' or '-'. You don't have to memorize this equation, just try to understand some basic charicteristics. Just looking at the equation, you would notice
If you represent the same equation in linear scale, it can be represented as follows. As I said, the equation shown above is in dB scale meaning 'Log' scale. If you convert the Log scale into linear scale with high school math, you should get the following equation.
By rearranging this equation, you can represent the same equation in many different forms as shown below. You would see many different form of this equation on various different document. It would take some time until you realize all those seeminly different equation basically mean same thing. (You can see an application of this equation in Path Loss Model in Free Space in Fading page).
Rule of Thumb
|
||