|
LDPC
LDPC stands for "Low-Density Parity-Check". It's a method used in communication systems for encoding and decoding data to detect and correct errors. LDPC codes are a type of linear error-correcting code that has found extensive application in modern communication technologies. LDPC codes are a powerful and efficient method for error correction in digital communication systems, enabling reliable data transmission even in challenging and noisy environments.
Here are some key points about LDPC:
- Error Correction: LDPC codes are particularly effective for correcting data transmission errors in noisy communication channels. They are used in scenarios where accurate data transmission is critical, such as in satellite communication, wireless networks, and data storage.
- Sparse Parity-Check Matrix: The 'low-density' in LDPC refers to the parity-check matrix used in these codes, which has a relatively small number of non-zero elements. This sparsity is what makes LDPC codes computationally efficient for error correction.
- Decoding Algorithm: LDPC codes are usually decoded using iterative probabilistic decoding algorithms, such as the belief propagation (BP) algorithm. These algorithms are efficient and can handle a large number of errors.
- Applications: LDPC codes are widely used in modern communication standards, including Wi-Fi (as part of the IEEE 802.11 standard), 5G cellular networks, and digital television (DVB-T2 and DVB-S2).
- History and Development: LDPC codes were first introduced by Robert G. Gallager in his doctoral dissertation at MIT in 1960. However, they were not widely used until the 1990s when advancements in digital technology made their implementation more feasible.
- Performance: LDPC codes are known for their near-Shannon-limit performance. The Shannon limit is a theoretical maximum efficiency for data communication in a channel with a given level of noise.
This note is about LDPC with the perspective of the implementation in 5G/NR. Followings are the topics to be covered in this note
NOTE : However in detail I try to describe the process, it would not be enough to understand every single step of this process unless you really try things on yourself. But implementing these kind of thing on our own is a huge challenge. As a stepping stone between high level conceptual understand and real implementation, I wrote a simulation based tutorial for this process with the help of AI (Gemini and Cursor). This tutorial would show you step by step process from Transport
Block Size to
a complete H matrix, even complete system equation H c = 0. Check out this note.
NR selected LDPC for the data channels (PDSCH and PUSCH ) due to its excellent performance and suitability for high-throughput, parallel processing.
High Level Procedure of LDPC Encoding
This is about LDPC encoding process at the very highlevel based on my own understanding.
This procedure shows that NR LDPC encoding is not a single fixed code. It is a structured family of codes. The encoder first treats the transport block as the input constraint. It then chooses the LDPC “template” that best fits that constraint, so the same physical mechanism can support very different TBS and code-rate points without redefining the whole parity-check matrix every time.
The key idea is the separation between a small base graph and a large practical matrix. The base graph is the high-level structure that defines how variable nodes and check nodes are connected. Once the base graph is decided, the encoder does not build a brand-new design from scratch. It “lifts” the base graph by a lifting size, so each base-graph entry expands into a block made of circularly shifted identity matrices. This is how the final H matrix becomes large enough for real
payload sizes while keeping the structure regular and implementation-friendly.
After that, encoding becomes a constraint satisfaction problem in a very concrete form. You are looking for a codeword vector c that makes all parity checks pass, which is expressed as H · c = 0. So the whole flow can be viewed as: pick the right structural template for the target operating point, scale it up using a standardized lifting rule, and then generate parity bits so the resulting codeword satisfies the parity-check equations.
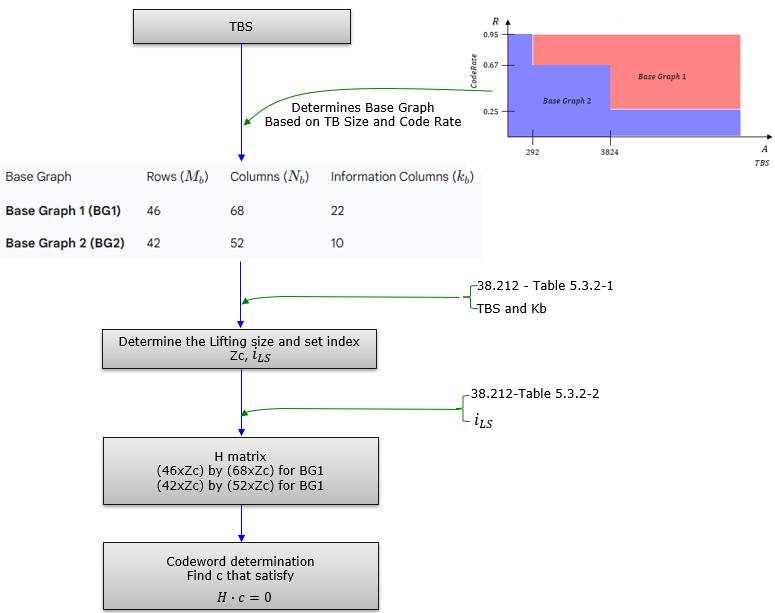
Now let me verbalize this diagram and it goes as follows
- Overall flow (what the diagram is trying to teach)
- Start from a payload requirement (TBS) and a protection requirement (code rate)
- Choose a standardized LDPC “template” (Base Graph)
- Scale that template to the exact needed size (Lifting)
- Build the parity-check matrix H from the lifted structure
- Encode by finding a codeword c that satisfies the parity constraints
- 1) Input: TBS
- TBS is the anchor parameter
- It represents the amount of transport data to be protected by LDPC
- TBS is used together with code rate
- Because “small vs large block” and “low vs high rate” drive different best structures
- 2) Base Graph selection (BG1 vs BG2)
- Base Graph is selected based on TBS and code rate
- The figure emphasizes a region split where BG2 tends to cover smaller / different rate regions and BG1 covers larger / other regions
- The Base Graph defines the mother structure size
- BG1 has its own (Mb, Nb, kb)
- BG2 has its own (Mb, Nb, kb)
- Practical meaning
- This step decides the “shape” of the LDPC code before any scaling happens
- 3) Lifting decision (Zc, iLS)
- Once BG is fixed, choose the lifting size
- Zc is the expansion factor
- Choose the lifting set index
- iLS selects which standardized lifting size entry is used
- Practical meaning
- This step turns “one base template” into “many usable code sizes” in a controlled way
- 4) Construct the full parity-check matrix H
- Build H by lifting the base graph
- Each base-graph entry expands into a Zc × Zc block
- Either a zero block or a shifted-identity type block
- Resulting matrix dimensions scale with Zc
- For BG1: (46 · Zc) × (68 · Zc)
- For BG2: (42 · Zc) × (52 · Zc)
- Practical meaning
- The base graph gives the pattern, lifting gives the real size
- 5) Codeword determination (encoding constraint)
- Encoding is framed as satisfying parity checks
- Find codeword c such that H · c = 0
- Practical meaning
- Parity bits are chosen so the final vector lies in the valid LDPC code space defined by H
Core Principle - Sparsity
Simply put, the final goal of LDPC is to find out parity bits that satisfy the following equation: H × cT = 0 (modulo 2). This equation is the foundation of Low-Density Parity-Check (LDPC) codes, ensuring that a codeword c adheres to the parity-check constraints defined by the parity-check matrix H. The example in the image illustrates this principle through the encoding process,
where
the objective is to compute parity bits p given information
bits s, such that the resulting codeword c satisfies this equation. Let’s elaborate on this as the core principle of LDPC, particularly in the context of 3GPP’s 5G NR, and explore its broader significance.
- LDPC codes are defined by a parity-check matrix (H). This matrix is "low-density," meaning it contains very few '1's and mostly '0's.
- Each row in H represents a parity-check equation, which is a simple XOR sum of a subset of the transmitted bits (codeword bits) that must equal zero for a valid codeword.
- Each column corresponds to a specific bit in the codeword.
- The sparsity is crucial because it allows for efficient iterative decoding algorithms.
As a simple example, let's assume that we have a data s = [s1, s2, s3, s4] = [1, 0, 1, 1], meaning there are 4 bits of data (k = 4) and want to encode this to a codeword c = [s1, s2, s3, s4, p1, p2, p3, p4]. The final goal of LDPC is to find the p1, p2, p3, p4 to meet the condition
H × cT = 0 (modulo 2).
The complicated part of LDPC in real application (as in 5G) is about how to construct H matrix and How to decode the received LDPC data into original message.
NOTE :If We Define the Precondition to H × cT = 1, It Would Not Work?
You're asking an interesting question about modifying the fundamental condition of LDPC codes from H × cT = 0 to H × cT = 1. Let’s explore why this change would not work in the context of LDPC codes, particularly as they are implemented in 3GPP’s 5G NR, and what the practical implications would be.
Understanding the Standard Condition: H × cT = 0
In LDPC codes (and linear block codes in general), the condition H × cT = 0 (with operations in GF(2), i.e., modulo 2) ensures that the codeword c satisfies all parity-check equations defined by the parity-check matrix H. This condition is fundamental for several reasons:
- Parity Checks: Each row of H represents a parity-check equation. For example, if a row of H has 1s in positions 1, 3, and 5, the corresponding equation is c1 + c3 + c5 = 0, meaning the sum of those bits (modulo 2) must be 0 (an even number of 1s).
- Error Detection: At the receiver, if H × rT ≠ 0 for a received vector r, it indicates errors, and the decoder uses this to correct them.
- Systematic Structure: The condition allows for systematic encoding, where the codeword c contains the original information bits plus parity bits that make the parity checks hold.
This setup ensures that the code has a well-defined structure, enabling efficient encoding, decoding, and error correction.
What Happens If We Change to H × cT = 1?
If we redefine the condition to H × cT = 1, we’re fundamentally altering the rules of the code. Let’s break down why this wouldn’t work:
- Linear Codes: LDPC codes are linear block codes, meaning the set of valid codewords forms a vector space (a subspace of {0,1}n). For a linear code, the all-zero codeword c = [0, 0, …, 0] must always be a valid codeword because it trivially satisfies H × 0T = 0.
- With H × cT = 1:
- If c = [0, 0, …, 0], then H × 0T = 0, which does not equal 1. So, the all-zero codeword would not be valid.
- This violates the linearity property, as the set of codewords would no longer form a vector space (since the zero vector is not included).
- Practical Impact: Linearity is crucial for efficient encoding and decoding. Without it, many standard algorithms (like syndrome decoding or belief propagation in LDPC) would break down.
- Standard Case (H × cT = 0): Each row of H enforces a parity check where the sum of the bits (where H has 1s) must be even (0 modulo 2). For example, if a row of H is [1, 0, 1, 0, 1, 0, 0, 0], the equation is c1 + c3 + c5 = 0.
- Modified Case (H × cT = 1): Now, each row would require the sum of the bits to be odd (1 modulo 2). For the same row, the equation becomes c1 + c3 + c5 = 1.
- Problem: If H has m rows, then H × cT = 1 means every parity check must result in 1 (an odd sum). This creates a highly constrained system:
- The equations may not have a solution for all input data. For example, if two rows of H are identical (e.g., both enforce c1 + c3 + c5 = 1), they cannot both be satisfied simultaneously because they would require the same sum to be both odd and odd, but there’s only one sum.
- In general, the system of equations H × cT = [1, 1, …, 1]T (an all-1 vector of length m) is over-constrained and often has no solution, especially if the rows of H are not carefully designed to ensure solvability.
- Standard Encoding: In LDPC (e.g., in 3GPP), we compute parity bits to satisfy H × cT = 0. This is straightforward because the equations are homogeneous (equal to 0), and we can solve for the parity bits systematically.
- Modified Encoding: With H × cT = 1, the equations become non-homogeneous (equal to 1). Solving for parity bits becomes much harder:
- The system H × cT = [1, 1, …, 1]T may not have a solution, as mentioned above.
- Even if a solution exists, it may not be unique, leading to ambiguity in encoding.
- Practical Impact: In 3GPP, encoding needs to be fast and deterministic for high-throughput applications (e.g., 5G’s multi-Gbps rates). An unsolvable or ambiguous system would make encoding impractical.
- Standard Decoding: LDPC decoding (e.g., Belief Propagation) relies on the syndrome H × rT. If H × rT = 0, the received vector r is a valid codeword. If not, the non-zero syndrome guides the iterative correction process.
- Modified Decoding: If the goal is H × rT = 1, the decoding process becomes problematic:
- The syndrome would be computed as H × rT ⊕ [1, 1, …, 1]T, but the iterative message-passing algorithms (like Belief Propagation) are designed for the H × cT = 0 framework.
- The Tanner graph (used for decoding) assumes that check nodes enforce even parity (sum = 0). Changing this to odd parity (sum = 1) for all checks disrupts the algorithm’s convergence properties.
- Practical Impact: In 5G NR, decoding must be efficient and reliable. The modified condition would make error correction either impossible or extremely inefficient.
- Standard Case: If a received vector r has errors, H × rT ≠ 0, and the non-zero syndrome helps identify and correct errors.
- Modified Case: If the goal is H × rT = 1, the syndrome check becomes H × rT ≟ [1, 1, …, 1]T. But since the system is often unsolvable, it’s unclear how to interpret deviations from this condition, making error detection and correction unreliable.
Could It Work in a Different Context?
The condition H × cT = 1 resembles a non-homogeneous system, which isn’t typical for linear block codes but could be interpreted in other coding schemes:
- Affine Codes: Instead of a linear code (where the codewords form a vector space), you could define an affine code, where the codewords are an affine subspace (a linear subspace shifted by a fixed vector). This would mean H × cT = b, where b is a fixed non-zero vector (e.g., [1, 1, …, 1]T). However:
- This is not how LDPC codes are defined in 3GPP or in standard practice.
- It loses the benefits of linearity, making encoding and decoding much harder.
- Modified Parity Checks: You could design a code where some parity checks result in 1 instead of 0, but this would require a different H matrix and a modified decoding algorithm, which isn’t compatible with standard LDPC frameworks like those in 5G NR.
Practical Implications in 3GPP
In 3GPP’s 5G NR, LDPC codes rely on H × cT = 0 for:
- Efficient Encoding: The quasi-cyclic structure of H (using base graphs and lifting) allows fast computation of parity bits.
- Reliable Decoding: Iterative decoding (Belief Propagation) is optimized for the H × cT = 0 condition, ensuring high throughput and low error rates.
- Error Detection: The syndrome check H × rT = 0 is critical for detecting and correcting errors in noisy channels.
Changing to H × cT = 1:
- Breaks the linearity of the code, making standard LDPC algorithms unusable.
- Makes encoding and decoding infeasible or inefficient, which is unacceptable for 5G’s high-speed, reliable communication requirements.
- Disrupts the entire error correction framework, leading to unreliable data transmission.
Summary
The condition H × cT = 1 would not work for LDPC codes as defined in 3GPP or in standard practice because:
- It violates the linearity of the code, breaking fundamental properties.
- It creates an over-constrained system that often has no solution, making encoding impossible.
- It disrupts standard decoding algorithms, rendering error correction inefficient or infeasible.
- It loses the practical benefits (efficiency, reliability) that make LDPC codes suitable for 5G NR.
The H × cT = 0 condition is not arbitrary—it’s a cornerstone of linear block codes like LDPC, ensuring they are practical and effective for real-world communication systems. If you’d like to explore alternative coding schemes where non-homogeneous conditions might apply, let me know!
LDPC Implementation in 5G - Structure
- Quasi-Cyclic LDPC (QC-LDPC): 3GPP uses a specific structure called QC-LDPC. This structure makes hardware implementation much more efficient and manageable. The large parity-check matrix (H) is constructed from smaller sub-matrices which are either zero matrices or circulant permutation matrices (identity matrices with columns cyclically shifted).
- Base Graphs (BG): 3GPP defines two fundamental Base Graphs, BG1 and BG2.
- BG1: Designed for larger data blocks and generally higher code rates.
- BG2: Designed for smaller data blocks and generally lower code rates.
- The choice between BG1 and BG2 depends on the transport block size and the target code rate.
- Lifting: The actual parity-check matrix used for encoding/decoding is generated by "lifting" the selected Base Graph (BG1 or BG2). This involves replacing each '1' in the base graph matrix with a specific circulant permutation matrix (based on shifts defined in the standard) of size ZxZ, and each '0' with a ZxZ zero matrix. The value 'Z' is called the lifting size, and it's chosen from a set of predefined values based on the required code block
length. This lifting process creates the larger, final QC-LDPC parity-check matrix H.
- Code Block Segmentation: If a transport block (the data coming from higher layers) is very large, it's first segmented into smaller code blocks. A CRC (Cyclic Redundancy Check) is added to each code block before LDPC encoding. Each code block is then encoded independently using LDPC. This limits the maximum complexity of the LDPC encoder/decoder.
Encoding
While LDPC codes are defined by the parity-check matrix H, encoding isn't as straightforward as with some other codes. 3GPP defines specific efficient encoding procedures based on the structured nature (QC-LDPC) of the codes. Essentially, given the information bits, the encoder calculates the necessary parity bits such that the resulting codeword (information bits + parity bits) satisfies all the parity-check equations defined by H (i.e., H * cT = 0, where c
is the codeword vector).
Rate Matching
Wireless systems need to adapt the coding rate (ratio of information bits to total transmitted bits) based on channel conditions. LDPC in 3GPP uses a flexible rate matching procedure.
- A base LDPC code (often low-rate) is generated.
- To achieve the desired code rate for transmission, some coded bits (usually parity bits, but sometimes information bits too for very high rates) are selected for transmission, while others are punctured (not transmitted) or shortened. For lower rates, bits might be repeated.
- 3GPP uses a circular buffer approach. All encoded bits (systematic/information and parity) are written into a buffer. Bits are then read out sequentially (and cyclically if needed) from this buffer for transmission, selecting the exact number of bits needed to match the allocated radio resources and target code rate.
Decoding
At the receiver, an iterative decoding algorithm is used, typically the Belief Propagation (also known as Sum-Product) algorithm or a variation like Min-Sum.
- This algorithm works on the Tanner Graph representation of the LDPC code (a bipartite graph connecting variable nodes representing codeword bits and check nodes representing parity-check equations).
- The decoder passes messages (probabilities or log-likelihood ratios) back and forth between variable nodes and check nodes along the edges of the Tanner graph.
- In each iteration, the nodes update their belief about the value of each received bit based on the messages received from their neighbours and the received signal strength for that bit.
- This process repeats for a fixed number of iterations or until the decoded bits form a valid codeword (i.e., satisfy all parity-check equations) or converge.
- The parallel nature of message passing across the sparse graph makes LDPC decoding suitable for high-speed hardware implementation.
QC-LDPC is a specific type of Low-Density Parity-Check (LDPC) code where the parity-check matrix (H) has a special, structured form. Instead of being an arbitrary sparse matrix, it's constructed from smaller square blocks, each of which is either a zero matrix or a circulant permutation matrix (CPM).
Key Concepts
1. LDPC Recap: Remember that LDPC codes are defined by a sparse parity-check matrix H. A vector c is a valid codeword if H * cT = 0. Sparsity allows for efficient iterative decoding.
2. Cyclic Codes: In a strictly cyclic code, if you cyclically shift a valid codeword, you get another valid codeword. QC-LDPC is a generalization.
3. Circulant Permutation Matrix (CPM): This is the fundamental building block. A CPM is a square matrix (say, size Z x Z) where each row is a cyclic shift of the row above it. Crucially, each row and column has exactly one '1' and the rest '0's. They are essentially cyclically shifted identity matrices.
- The identity matrix (I) is a CPM (zero shift).
- A cyclically shifted identity matrix is a CPM. For example, shifting the 3x3 identity matrix
I_3 right by one position gives:
I3 =
Shifted(I3, 1) =
- The zero matrix (all zeros) is often considered trivially in this context as well, representing the absence of connections in the Tanner graph.
4. Quasi-Cyclic Structure: The "Quasi" part means the entire H matrix isn't necessarily cyclic, but it *is* composed of these CPM blocks (and zero blocks). If you divide the H matrix into ZxZ blocks, each block is a CPM or a zero matrix.
How is the H Matrix Constructed?
Often, a QC-LDPC matrix H is defined by:
1. A Lifting Factor (or Expansion Factor) Z: This defines the size (Z x Z) of the circulant blocks.
2. A Base Matrix (or Model Matrix) B: This is a smaller matrix whose entries tell you which CPM to place in the corresponding block position in the final H matrix.
- An entry
s (where s >= 0) in the base matrix means: place the ZxZ identity matrix cyclically shifted by s positions in that block location.
- A special entry (e.g., -1 or ∞, depending on convention) means: place the ZxZ zero matrix in that block location.
If the Base Matrix B has dimensions M_b x N_b, and the lifting factor is Z, the final QC-LDPC matrix H will have dimensions (M_b * Z) x (N_b * Z).
Example
Let's construct a small QC-LDPC matrix H.
Choose Lifting Factor Z = 3.
Define a Base Matrix B (size 2x4): Base Matrix refers to the matrix representation of what is called 'Base Graph' in 3GPP.
This is just an example of the simple Base Matrix. This is a Base Matrix (B) used to define the structure of a Quasi-Cyclic LDPC (QC-LDPC) parity-check matrix (H).
This matrix doesn't directly contain message data. Instead, each number tells you how to construct a block within the larger, final parity-check matrix H. You need a Lifting Factor (Z) (which was Z=3 in the previous example) to interpret these numbers:
- Non-negative numbers (
0, 1, 2): These numbers represent a cyclic shift applied to a ZxZ identity matrix.
0: Represents the ZxZ identity matrix with no shift (P0).1: Represents the ZxZ identity matrix cyclically shifted right by 1 position (P1).2: Represents the ZxZ identity matrix cyclically shifted right by 2 positions (P2).- In general, a non-negative number
s represents the ZxZ identity matrix shifted s times (Ps).
- Negative number (
-1): As the text below the matrix in the image notes, the convention here is that -1 represents the Z x Z zero matrix (0_Z). This means this block position in the final H matrix will consist entirely of zeros. (Sometimes other conventions like using infinity are used for the zero matrix).
Now, we need the 3x3 circulant permutation matrices corresponding to the shifts 0, 1, and 2, plus the 3x3 zero matrix:
Now, substitute these blocks into H according to the base matrix B:
Block Col 1 | Block Col 2 | Block Col 3 | Block Col 4
H = [ P0 | P2 | 0_3 | P1 ] Block Row 1
[-------------+--------- ---+-------------+-----------]
[ P1 | 0_3 | P2 | P0 ] Block Row 2
Writing this out fully:
This resulting H matrix is:
- Sparse: It has relatively few '1's.
- Quasi-Cyclic: It's built from 3x3 circulant (or zero) blocks. The dimensions are (2 * 3) x (4 * 3) = 6 x 12.
Why Use QC-LDPC?
- Hardware Implementation Efficiency: The regular structure is extremely beneficial for hardware (like FPGAs or ASICs). Encoding and especially decoding can be implemented using parallel shift-register-based architectures, making them fast and efficient. Memory addressing is simplified.
- Efficient Encoding: While general LDPC encoding can be complex, the structure of QC-LDPC allows for more efficient encoding algorithms (often based on linear feedback shift registers).
- Compact Representation: You only need to store the base matrix and the lifting factor Z to define a potentially very large H matrix. This is how standards like 5G NR and Wi-Fi define their LDPC codes – specifying base graphs (matrices) and allowed lifting sizes.
- Scalability: A single base graph can generate a family of codes with different lengths just by changing the lifting factor Z.
In essence, QC-LDPC codes offer the excellent error-correction performance associated with LDPC codes while having a structure that makes them much more practical and efficient to implement in real-world communication systems.
Lifting is the process used in QC-LDPC code construction to expand a small Base Graph (represented by a Base Matrix B) into the final, much larger parity-check matrix H.
It works like this: You start with a Base Matrix B (like the 2x4 example B we discussed) and choose a Lifting Factor Z (also called Lifting Size or Expansion Factor), which is a positive integer (e.g., Z=3 in the previous example). Then, you replace each entry in the Base Matrix B with a Z x Z block matrix according to these rules:
- If an entry in
B is a non-negative integer s (representing a shift), you replace it with the Z x Z identity matrix cyclically shifted s times (Ps).
- If an entry in
B represents the zero block (e.g., -1 in the convention used), you replace it with the Z x Z zero matrix (0_Z).
The result is the final parity-check matrix H. If the Base Matrix B has dimensions M_b x N_b, the lifted matrix H will have dimensions (M_b * Z) x (N_b * Z).
NOTE: The 2x4 Base Matrix B in the example of previous section was lifted with Z=3 to create the 6x12 parity-check matrix H.
Why is Lifting Needed?
Lifting is a crucial technique used in modern communication standards (like 5G, Wi-Fi) for several important reasons:
- Code Scalability and Flexibility: This is arguably the most significant benefit. Communication systems need to handle data blocks of many different sizes. Instead of designing a completely new LDPC code (and a new H matrix) for every possible size, lifting allows a single Base Graph to generate a whole family of codes with different lengths. By simply choosing a different Lifting Factor
Z from a predefined set, you can create a valid LDPC
code tailored to
the required block size.
- Compact Code Definition: Standards like 3GPP don't need to specify enormous H matrices for every scenario. They only need to define a few relatively small Base Graphs (like BG1 and BG2) and a set of allowed Lifting Factors (
Z values). This makes the standard much more compact and manageable.
- Maintaining Good Code Properties: The Base Graphs are carefully designed to have good structural properties (like large girth in their Tanner graph representation) which are important for the performance of the iterative LDPC decoder. The lifting process is designed to preserve these beneficial properties in the final, larger H matrix.
- Efficient Hardware/Software Implementation: The highly structured nature of the lifted matrix
H (composed of repeating patterns of shifted identity matrices and zero matrices) lends itself well to efficient implementation. Decoders can leverage this structure using parallel processing, shift registers, and optimized memory access patterns. The underlying logic can often be reused regardless of the specific lifting factor Z chosen.
- System Adaptability: Wireless communication requires constant adaptation to changing channel conditions and data requirements. Lifting provides an efficient mechanism for the physical layer to generate the appropriate LDPC code (with the right length and corresponding parity-check matrix H) on the fly by selecting the necessary lifting factor
Z based on the current transmission parameters.
In summary, lifting provides an elegant and efficient way to generate families of high-performing LDPC codes of various lengths from a small set of core designs (the Base Graphs), which is essential for the flexibility and efficiency required in modern communication systems.
Lifting Table for 5G LDPC
The process of selecting the lifting size Zc in the context of LDPC is a critical step in the encoding procedure for 5G New Radio (NR)but it took me several years for me to understand the overall concept of the selection of a specific Listing size. The lifting size Zc determines how the base graph (a small, predefined matrix) is expanded into a larger parity-check matrix H that is used for encoding. Let’s break down the selection
process based on
the document.
Key Parameters and Context
- LDPC Base Graphs: The document mentions two LDPC base graphs:
- Base Graph 1: Used when the code block length K ≤ 8448. It has 46 rows and 68 columns.
- Base Graph 2: Used when K > 8448. It has 42 rows and 52 columns.
- Input Bit Sequence: The input to the encoder is a bit sequence c0, c1, c2, ..., cK-1, where K is the number of bits to encode.
- Output After Encoding: The encoded bits are denoted as d0, d1, d2, ..., dN-1, where N is the total number of encoded bits.
- Lifting Size Zc: This is a scaling factor that "lifts" the base graph into a larger parity-check matrix H. The value of Zc is chosen from a predefined set in a table (referred to as Table 5.3.2-1 in the 3GPP document).
- Dimensions After Lifting:
- For Base Graph 1: N = 66Zc, since the base graph has 66 columns.
- For Base Graph 2: N = 50Zc, since the base graph has 50 columns.
The lifting size Zc must be chosen such that the base graph can accommodate the input bit sequence of length K, and the resulting parity-check matrix H can be used for encoding.
Step-by-Step Process for Selecting Zc
The selection of Zc is described in Step 1 and Step 2 of the encoding procedure in the document. Let’s go through these steps in detail:
Step 1: Find the Set with Index iLS in Table 5.3.2-1 that Contains Zc
- The 3GPP standard defines a table (Table 5.3.2-1) that contains sets of possible lifting sizes Zc. Each set is indexed by iLS, and the sets contain different values of Zc.
- The lifting size Zc is not explicitly given in the problem statement but is typically determined based on the input length K and the base graph being used. The goal of this step is to identify which set in the table contains the appropriate Zc.
Step 2: For k = 22Zc to K-1, Perform the Following
- The value k = 22Zc represents the number of information bits that the base graph can handle after lifting by Zc. This comes from the structure of the base graph:
- Both LDPC base graphs have 22 columns dedicated to information bits (the remaining columns are for parity bits).
- When the base graph is lifted by Zc, each column corresponds to Zc bits, so the number of information bits that can be encoded is 22Zc.
- The condition k = 22Zc to K-1 checks whether the lifted base graph can accommodate the input bit sequence of length K. In other words, we need 22Zc ≥ K to ensure the base graph can handle all K bits.
- If ck ≠ NULL:
- If the bit ck at position k (for k ranging from 22Zc to K-1) is not a NULL bit (i.e., it’s an actual information bit), then the current Zc is too small to accommodate all K bits.
- In this case, set:
- dk-22Zc = ck: This means the bits beyond 22Zc are copied into the output sequence d, effectively shortening the input sequence to fit the base graph.
- Else:
- If ck = NULL, the bit at position k is a filler bit (used for padding).
- Set:
- ck = 0: Replace the NULL bit with 0.
- dk-22Zc =: Mark the corresponding position in the output as NULL.
Implicit Selection of Zc
- The document doesn’t explicitly show the selection of Zc, but the process is implied through the condition 22Zc ≥ K.
- To select Zc:
- Compute the minimum Zc such that 22Zc ≥ K.
- From the set of possible Zc values in Table 5.3.2-1, choose the smallest Zc that satisfies this condition.
- For example:
- If K = 5000, then 22Zc ≥ 5000, so Zc ≥ ⌈5000 / 22⌉ = 228.
- You would then look in Table 5.3.2-1 for the smallest Zc ≥ 228 in the appropriate set (determined by iLS).
Additional Details
- Table 5.3.2-1: This table contains sets of lifting sizes. Typically, in 3GPP LDPC, the lifting sizes are grouped into sets like {2, 4, 8, 16, ...}, {3, 6, 12, 24, ...}, etc., and the set index iLS is determined based on the code block length K and the base graph.
- Base Graph Selection:
- If K ≤ 8448, use Base Graph 1.
- If K > 8448, use Base Graph 2.
- The choice of base graph affects the number of information columns (always 22 for both graphs) and the total number of columns (66 for Base Graph 1, 50 for Base Graph 2), which in turn affects N.
- Matrix H: The parity-check matrix H is constructed by lifting the base graph HBG using Zc. Each element in HBG is replaced as follows:
- A 0 in HBG becomes an all-zero matrix of size Zc × Zc.
- A 1 in HBG becomes a circular permutation matrix I(Pi,j) of size Zc × Zc, where Pi,j is a shift value determined by the base graph and Zc.
Summary of Zc Selection
- Determine the Base Graph:
- Use Base Graph 1 if K ≤ 8448.
- Use Base Graph 2 if K > 8448.
- Compute the Minimum Zc:
- Calculate the smallest Zc such that 22Zc ≥ K.
- Select Zc from Table 5.3.2-1:
- Look up Table 5.3.2-1 and find the set indexed by iLS.
- Choose the smallest Zc in that set that satisfies 22Zc ≥ K.
- Handle Padding or Shortening:
- If K < 22Zc, pad the input with NULL bits (which are later set to 0).
- If K > 22Zc, shorten the input by copying bits into the output sequence d.
Example
Suppose K = 5000, and we’re using Base Graph 1 (since K ≤ 8448):
- Compute Zc:
- 22Zc ≥ 5000
- Zc ≥ ⌈5000 / 22⌉ = 228.
- Assume Table 5.3.2-1 has a set with Zc values like {208, 224, 240, 256, ...}.
- The smallest Zc ≥ 228 is 240.
- So, Zc = 240, and the number of information bits the base graph can handle is 22 × 240 = 5280, which is greater than K = 5000. The remaining 5280 - 5000 = 280 bits are padded with NULLs (later set to 0).
Inter-relation among Table 5.3.2-1, Table 5.3.2-2 and Table 5.3.2-3
They are interrelated because they collectively define the structure and parameters needed to construct the parity-check matrix H, which is used for encoding data in the LDPC process. In short, the tables are tightly interrelated as part of the LDPC encoding process:
- Table 5.3.2-1 provides the foundational parameter Zc and the set index iLS.
- Tables 5.3.2-2 and 5.3.2-3 use Zc and iLS to define the structure of the base graph and the shift values needed to construct the parity-check matrix H.
- The choice between Tables 5.3.2-2 and 5.3.2-3 depends on the code block length K, but both rely on the parameters from Table 5.3.2-1 to complete the encoding process.
Here’s how they connect:
Table 5.3.2-1 Provides the Lifting Size Zc, Which is Used by Tables 5.3.2-2 and 5.3.2-3
- Connection: The lifting size Zc from Table 5.3.2-1 is a key parameter needed to interpret the shift values Vi,j in Tables 5.3.2-2 and 5.3.2-3.
- Details:
- In the LDPC encoding process (as described in the document), the first step is to select a lifting size Zc from Table 5.3.2-1 based on the code block length K. This involves finding the set index iLS and the smallest Zc in that set such that 22Zc ≥ K.
- The selected Zc determines the size of the submatrices used to lift the base graph HBG into the full parity-check matrix H. Specifically, each element in HBG is replaced by a Zc × Zc submatrix.
- The shift values Vi,j in Tables 5.3.2-2 and 5.3.2-3 are used to compute the actual cyclic shift Pi,j for each submatrix, where Pi,j = mod(Vi,j, Zc). This means Zc from Table 5.3.2-1 directly affects how the shift values in Tables 5.3.2-2 and 5.3.2-3 are applied.
Tables 5.3.2-2 and 5.3.2-3 Depend on the Set Index iLS from Table 5.3.2-1
- Connection: The shift values Vi,j in Tables 5.3.2-2 and 5.3.2-3 are specified for each set index iLS, which is determined when selecting Zc from Table 5.3.2-1.
- Details:
- Table 5.3.2-1 is organized into sets, each with an index iLS. When Zc is selected, the corresponding iLS is also determined.
- Tables 5.3.2-2 and 5.3.2-3 provide Vi,j values for each position (i, j) where HBG is 1, and these values are given for each possible iLS. This means that once iLS is chosen from Table 5.3.2-1, it dictates which set of Vi,j values to use from Tables 5.3.2-2 or 5.3.2-3, depending on the base graph.
Tables 5.3.2-2 and 5.3.2-3 Define the Base Graphs, Which Are Lifted Using Zc
- Connection: Tables 5.3.2-2 and 5.3.2-3 provide the structure of the base graphs (HBG) and the shift values Vi,j, which are used in conjunction with Zc to construct the final parity-check matrix H.
- Details:
- The base graph HBG (from Table 5.3.2-2 for Base Graph 1 or Table 5.3.2-3 for Base Graph 2) is a small binary matrix that defines the connections between check nodes and variable nodes.
- To create the full parity-check matrix H, each element in HBG is replaced as follows:
- A 0 in HBG is replaced by an all-zero matrix of size Zc × Zc.
- A 1 in HBG is replaced by a circular permutation matrix I(Pi,j) of size Zc × Zc, where Pi,j = mod(Vi,j, Zc).
- Here, Zc (from Table 5.3.2-1) determines the size of the submatrices, and Vi,j (from Table 5.3.2-2 or 5.3.2-3) determines the shift for each submatrix.
Base Graph Selection Affects Which Table (5.3.2-2 or 5.3.2-3) is Used
- Connection: The choice between Table 5.3.2-2 and Table 5.3.2-3 depends on the code block length K, but both tables use the same Zc and iLS from Table 5.3.2-1.
- Details:
- If K ≤ 8448, Base Graph 1 is used, so Table 5.3.2-2 provides the structure of HBG and the shift values Vi,j.
- If K > 8448, Base Graph 2 is used, so Table 5.3.2-3 provides the structure of HBG and the shift values Vi,j.
- In both cases, the Zc and iLS selected from Table 5.3.2-1 are used to interpret the Vi,j values and construct H.
Summary of Interrelations
- Table 5.3.2-1 is the starting point: It provides the lifting size Zc and the set index iLS, which are determined based on the code block length K.
- Tables 5.3.2-2 and 5.3.2-3 depend on Zc and iLS:
- The set index iLS from Table 5.3.2-1 determines which set of Vi,j values to use from Table 5.3.2-2 (for Base Graph 1) or Table 5.3.2-3 (for Base Graph 2).
- The lifting size Zc from Table 5.3.2-1 is used to compute the actual shift Pi,j = mod(Vi,j, Zc) and to determine the size of the submatrices in the lifted matrix H.
- Tables 5.3.2-2 and 5.3.2-3 are alternatives based on the base graph:
- They provide the structure of HBG and the shift values Vi,j, but only one table is used at a time, depending on whether Base Graph 1 or Base Graph 2 is selected (based on K).
Flow of Dependency
- Determine K: The code block length K determines which base graph to use (Base Graph 1 if K ≤ 8448, Base Graph 2 if K > 8448).
- Select Zc and iLS from Table 5.3.2-1: Based on K, choose the smallest Zc such that 22Zc ≥ K, and note the corresponding set index iLS.
- Choose the Base Graph Table:
- If Base Graph 1, use Table 5.3.2-2.
- If Base Graph 2, use Table 5.3.2-3.
- Use iLS to Get Vi,j: From the chosen table (5.3.2-2 or 5.3.2-3), look up the Vi,j values corresponding to the set index iLS.
- Construct H: Use Zc to determine the size of the submatrices, and use Vi,j to compute the shifts Pi,j, thereby lifting HBG into H.
< 38.212-Table 5.3.2-1: Sets of LDPC lifting size Z >
The structure, role of this table can be described as below :
- Purpose: This table provides sets of possible lifting sizes Zc, which are used to scale the base graph into a larger parity-check matrix H.
- Structure: The table is organized into sets, each indexed by iLS (set index). Each set contains a range of Zc values. For example, a set might include values like {2, 4, 8, 16, ...}, {3, 6, 12, 24, ...}, etc.
- Role in LDPC: The lifting size Zc determines the size of the submatrices used to expand the base graph HBG. It is selected based on the code block length K (as explained in my previous response) to ensure the base graph can accommodate the input bits.
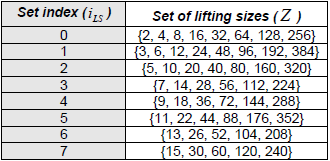
NOTE : This table can be generated by the rule : base_Z x 2^j , where base_Z = the first elements in the set, j = [0 7]
|
Set index (iLS)
|
base_Z
|
Set of lifting sizes (Z)
|
|
0
|
2
|
{2 · 20 = 2, 2 · 21 = 4, 2 · 22 = 8, 2 · 23 = 16,
2 · 24 = 32, 2 · 25 = 64, 2 · 26 = 128, 2 · 27 = 256}
|
|
1
|
3
|
{3 · 20 = 3, 3 · 21 = 6, 3 · 22 = 12, 3 · 23 = 24,
3 · 24 = 48, 3 · 25 = 96, 3 · 26 = 192, 3 · 27 = 384}
|
|
2
|
5
|
{5 · 20 = 5, 5 · 21 = 10, 5 · 22 = 20, 5 · 23 = 40,
5 · 24 = 80, 5 · 25 = 160, 5 · 26 = 320, 5 · 27 = 640}
|
|
3
|
7
|
{7 · 20 = 7, 7 · 21 = 14, 7 · 22 = 28, 7 · 23 = 56,
7 · 24 = 112, 7 · 25 = 224, 7 · 26 = 448, 7 · 27 = 896}
|
|
4
|
9
|
{9 · 20 = 9, 9 · 21 = 18, 9 · 22 = 36, 9 · 23 = 72,
9 · 24 = 144, 9 · 25 = 288, 9 · 26 = 576, 9 · 27 = 1152}
|
|
5
|
11
|
{11 · 20 = 11, 11 · 21 = 22, 11 · 22 = 44, 11 · 23 = 88,
11 · 24 = 176, 11 · 25 = 352, 11 · 26 = 704, 11 · 27 = 1408}
|
|
6
|
13
|
{13 · 20 = 13, 13 · 21 = 26, 13 · 22 = 52, 13 · 23 = 104,
13 · 24 = 208, 13 · 25 = 416, 13 · 26 = 832, 13 · 27 = 1664}
|
|
7
|
15
|
{15 · 20 = 15, 15 · 21 = 30, 15 · 22 = 60, 15 · 23 = 120,
15 · 24 = 240, 15 · 25 = 480, 15 · 26 = 960, 15 · 27 = 1920}
|
In the 3GPP TS 38.212 standard, the lifting sizes are capped at 384. The table above follows the mathematical "doubling" rule strictly, but in practical 5G implementation, values exceeding 384 are typically not used for these specific sets.
Removing the capped number, we can the following table which is same as 38.212 - Table 5.3.2-1
|
Set index (iLS)
|
base_Z
|
Set of lifting sizes (Z)
|
|
0
|
2
|
{2, 4, 8, 16, 32, 64, 128, 256}
|
|
1
|
3
|
{3, 6, 12, 24, 48, 96, 192, 384}
|
|
2
|
5
|
{5, 10, 20, 40, 80, 160, 320}
|
|
3
|
7
|
{7, 14, 28, 56, 112, 224}
|
|
4
|
9
|
{9, 18, 36, 72, 144, 288}
|
|
5
|
11
|
{11, 22, 44, 88, 176, 352}
|
|
6
|
13
|
{13, 26, 52, 104, 208}
|
|
7
|
15
|
{15, 30, 60, 120, 240}
|
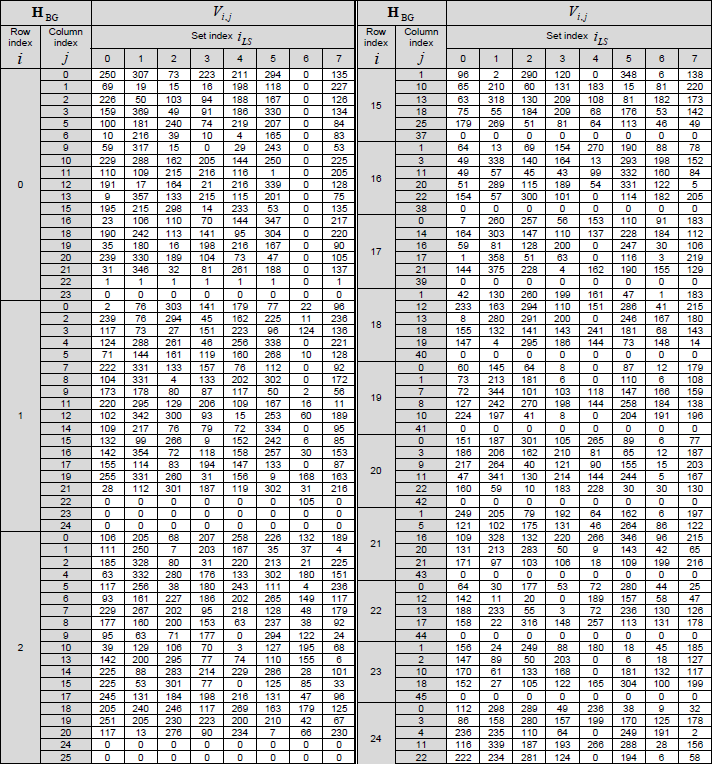
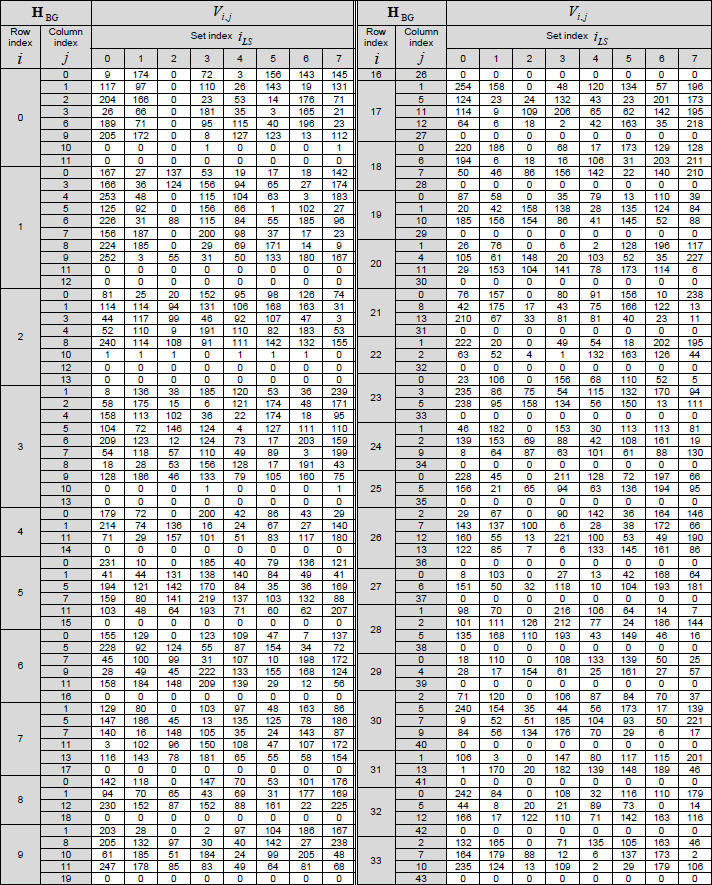
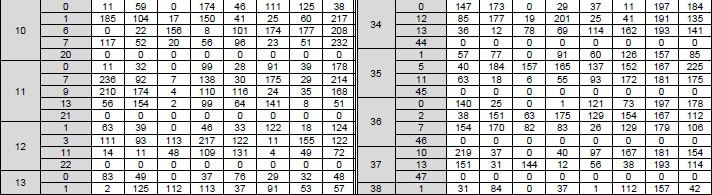
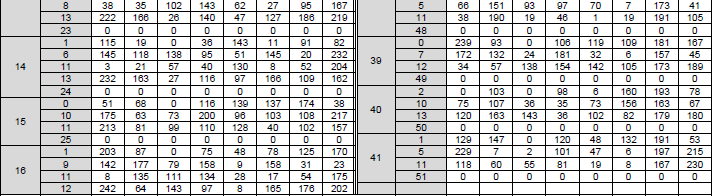
< 38.212-Table 5.3.2-2: LDPC base graph 1 (HBG) and its parity check matrices ( Vi,j) >
The structure, role of this table can be described as below :
- Purpose: This table defines the structure of LDPC Base Graph 1 and the associated shift values Vi,j.
- Structure:
- Base Graph 1 (HBG): A binary matrix with 46 rows (check nodes) and 68 columns (variable nodes). The first 22 columns correspond to information bits, and the remaining columns correspond to parity bits.
- Elements: The table specifies the positions (i, j) where HBG has a value of 1 (indicating a connection between a check node i and a variable node j). All other positions are 0.
- Shift Values (Vi,j): For each position (i, j) where HBG is 1, the table provides a shift value Vi,j. This value depends on the set index iLS (from Table 5.3.2-1) and is used to define the circular permutation matrix that replaces the 1 in the lifted matrix H.
- Role in LDPC: Base Graph 1 is used when the code block length K ≤ 8448. The shift values Vi,j are used to construct the parity-check matrix H by determining the cyclic shifts in the submatrices.
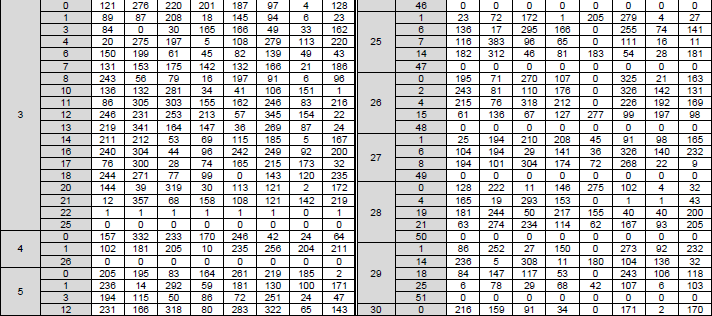
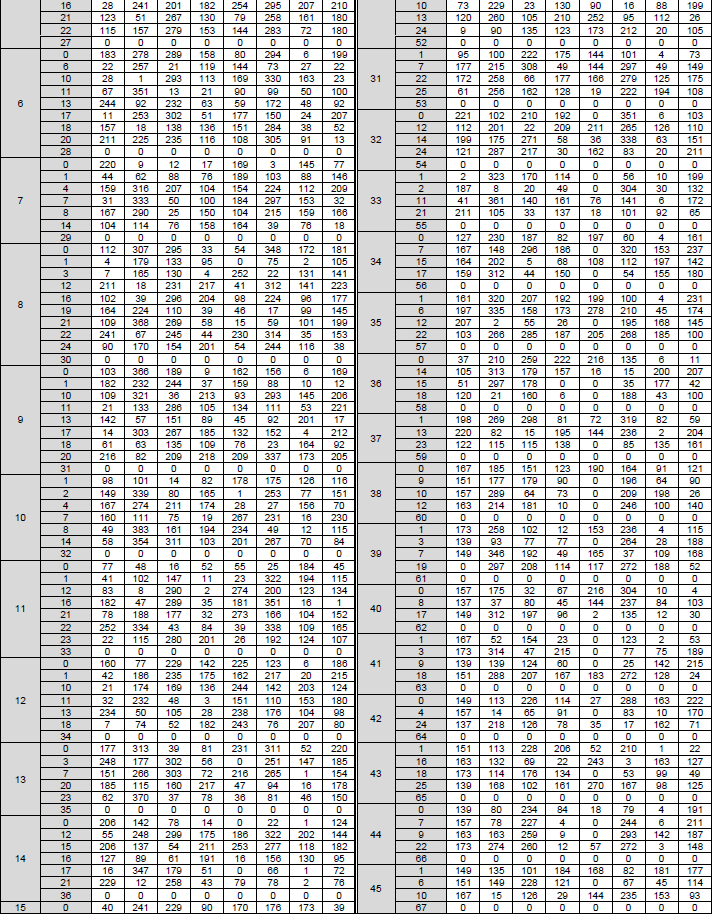
< 38.212-Table 5.3.2-3: LDPC base graph 2 (HBG) and its parity check matrices ( Vi,j) >
The structure, role of this table can be described as below :
Table 5.3.2-3: LDPC Base Graph 2 (HBG) and its Parity Check Matrices (Vi,j)
- Purpose: This table defines the structure of LDPC Base Graph 2 and the associated shift values Vi,j.
- Structure:
- Base Graph 2 (HBG): A binary matrix with 42 rows (check nodes) and 52 columns (variable nodes). The first 22 columns correspond to information bits, and the remaining columns correspond to parity bits.
- Elements: Similar to Table 5.3.2-2, this table specifies the positions (i, j) where HBG has a value of 1, with all other positions being 0.
- Shift Values (Vi,j): For each position (i, j) where HBG is 1, the table provides a shift value Vi,j, which also depends on the set index iLS.
- Role in LDPC: Base Graph 2 is used when the code block length K > 8448. The shift values Vi,j serve the same purpose as in Table 5.3.2-2, defining the cyclic shifts for the lifted matrix H.
LDPC (Low-Density Parity-Check) codes are compute-intensive primarily due to the iterative nature of their decoding process, the complexity of the operations involved, and the scale of the matrices used in modern systems like 3GPP’s 5G NR. While LDPC codes offer excellent error correction performance, their computational demands stem from several factors. Let’s break this down in detail, focusing on the encoding and decoding processes, and how they apply in the context of 3GPP.
Iterative Decoding Process
The primary reason LDPC is compute-intensive is its decoding algorithm, which typically uses an iterative message-passing approach, such as the Belief Propagation (BP) algorithm or its variants (e.g., Min-Sum algorithm). Here’s why this is computationally demanding:
- Tanner Graph Operations:
- LDPC decoding operates on a Tanner graph, a bipartite graph with variable nodes (representing codeword bits) and check nodes (representing parity-check equations from the H matrix).
- In each iteration, messages (usually log-likelihood ratios, LLRs) are passed between variable nodes and check nodes along the edges of the graph.
- For a codeword of length n, with m check nodes and an average degree of connectivity (number of 1s per row/column in H), the number of messages passed per iteration is proportional to the number of edges, which can be large (e.g., 3m to 5m).
- Multiple Iterations:
- The decoder typically runs for 10–50 iterations to converge to a solution (i.e., until H × cT = 0 or a maximum iteration limit is reached).
- Each iteration involves:
- Variable-to-Check Messages: Each variable node sends updated LLRs to connected check nodes.
- Check-to-Variable Messages: Each check node computes new LLRs based on the incoming messages and sends them back to variable nodes.
- These computations involve additions, comparisons, and sometimes nonlinear operations (e.g., in the Sum-Product algorithm, computing hyperbolic tangents or their approximations).
- For a codeword of length n = 8448 (a typical maximum in 5G NR Base Graph 1), with 50 iterations, the total number of operations can easily reach millions per codeword.
- In 3GPP:
- 5G NR uses large block lengths (up to 8448 bits for BG1) and high code rates, leading to large Tanner graphs.
- The high throughput requirements (e.g., tens of Gbps) mean the decoder must process many codewords per second, amplifying the computational load.
Large Parity-Check Matrix
The size and structure of the parity-check matrix H contribute to the computational intensity:
- Matrix Dimensions:
- In 3GPP 5G NR, the H matrix is derived from a base graph (e.g., 46×68 for BG1) and expanded by a lifting factor Z (up to 384). This results in an H matrix with dimensions like (46Z) × (68Z), or up to 17664 × 26112 for Z = 384.
- Even though H is sparse (low-density), the sheer size means there are still thousands of 1s, each corresponding to an edge in the Tanner graph.
- Message Updates:
- Each 1 in H represents an edge in the Tanner graph, requiring a message to be computed and passed in each iteration.
- For example, if a check node is connected to 10 variable nodes (a typical degree in 5G NR), it must process 10 incoming messages to compute 10 outgoing messages, often involving complex operations like minimum finding (in Min-Sum) or tanh computations (in Sum-Product).
- In 3GPP:
- The quasi-cyclic structure of H (using circulant submatrices) helps with parallelization, but the large size still demands significant computation, especially for high Z values used in high-throughput scenarios.
Floating-Point or Fixed-Point Arithmetic
- LLR Computations:
- During decoding, messages are typically LLRs, which are real numbers representing the likelihood of a bit being 0 or 1.
- In the Sum-Product algorithm, check node updates involve nonlinear operations like tanh and arctanh, which are computationally expensive.
- Even in the Min-Sum algorithm (a simpler approximation used in 5G NR), check node updates require finding the minimum of incoming LLR magnitudes and computing signs, which still involves comparisons and multiplications.
- Precision Requirements:
- To achieve good performance, LLRs are often represented with high precision (e.g., 6–8 bits in fixed-point implementations), increasing the computational cost of each operation.
- In hardware implementations (e.g., ASICs for 5G base stations), fixed-point arithmetic is used to reduce complexity, but this still requires careful design to avoid performance degradation.
- In 3GPP:
- The high data rates of 5G NR require decoders to process LLRs at extremely high speeds, often in parallel, which demands significant computational resources.
Encoding Complexity (Though Less Intensive Than Decoding)
While encoding is generally less compute-intensive than decoding in LDPC, it still contributes to the overall computational load:
- Parity Bit Computation:
- Encoding involves solving for parity bits such that H × cT = 0. In 3GPP, the H matrix is structured to make this efficient (e.g., using a lower-triangular form for the parity part), but it still requires matrix operations.
- For a codeword of length n with k information bits, the number of parity bits is n - k, and solving for them involves operations proportional to (n - k)2 in a naive implementation.
- In 3GPP:
- The quasi-cyclic structure of H allows encoding to be performed using shift registers, reducing complexity to roughly linear in n.
- However, for large block lengths (e.g., 8448 bits), encoding still requires significant computation, especially when processing many codewords per second.
High Throughput Requirements in 5G NR
- Real-Time Constraints:
- 5G NR targets data rates of tens of Gbps, meaning the decoder must process millions of bits per second.
- For a codeword of 8448 bits, at 10 Gbps, the decoder must handle over 1 million codewords per second, with each codeword requiring multiple iterations of message passing.
- Parallel Processing:
- To meet these throughput demands, LDPC decoders in 5G NR are highly parallelized, processing multiple nodes or layers of the Tanner graph simultaneously.
- While parallelism reduces latency, it increases the computational load, as more operations must be performed concurrently, requiring more hardware resources (e.g., in ASICs or FPGAs).
- HARQ Support:
- 5G NR uses Hybrid Automatic Repeat Request (HARQ), where retransmissions send additional parity bits. The decoder must combine these with previous transmissions, increasing the computational complexity of soft combining and decoding.
Memory and Data Movement
- Memory Access:
- LDPC decoding requires storing and accessing large amounts of data, including:
- The H matrix (or its compact representation in 3GPP).
- LLRs for each variable node.
- Messages passed along edges in each iteration.
- For a large H matrix (e.g., 17664×26112), even a sparse representation requires significant memory, and frequent memory accesses (to fetch and update messages) add to the computational burden.
- In 3GPP:
- The quasi-cyclic structure reduces memory requirements by storing only the base graph and shift values, but the high throughput still demands fast memory access, often a bottleneck in hardware implementations.
Mitigations in 3GPP
While LDPC is compute-intensive, 3GPP’s 5G NR design includes several optimizations to manage this complexity:
- Quasi-Cyclic Structure:
- The H matrix is constructed from circulant submatrices, enabling parallel processing and reducing memory usage.
- This allows hardware to process entire circulants (of size Z) in parallel, improving throughput.
- Layered Decoding:
- Instead of updating all check nodes simultaneously, 5G NR often uses layered decoding, where check nodes are grouped into layers (based on the base graph structure). This reduces memory conflicts and improves convergence speed.
- Min-Sum Algorithm:
- 5G NR typically uses the Min-Sum algorithm instead of the more complex Sum-Product algorithm, trading off some performance for lower computational complexity.
- Hardware Acceleration:
- 5G base stations and devices use dedicated hardware (e.g., ASICs, FPGAs) to parallelize LDPC decoding, meeting the real-time requirements.
Comparison to Other Codes
- Compared to Turbo codes (used in LTE), LDPC codes in 5G NR are more compute-intensive per iteration due to the larger block sizes and more complex message-passing. However, LDPC converges faster (fewer iterations) and has better performance at high code rates, making it a net win for 5G.
- Compared to Polar codes (used for 5G control channels), LDPC is more compute-intensive because Polar codes use a simpler successive cancellation decoding, though they are less effective for large block lengths.
Reference
[1] 3GPP TSG RAN WG1 #86 - R1-166414 Discussion on LDPC codes for NR
[2] 3GPP TSG RAN WG1 #86 R1-166769 Discussion on Length-Compatible Quasi-Cyclic LDPC Codes
[3] 3GPP TSG RAN WG1 #86 R1-166770 Discussion on Rate-Compatible Quasi-Cyclic LDPC Codes
[4] 3GPP TSG RAN WG1 #86 R1-166929 LDPC Code Design for NR
[5] 3GPP TSG-RAN WG1 #86 R1-167532 Discussion on LDPC coding scheme of code structure, granularity and HARQ-IR
[6] 3GPP TSG RAN WG1 #86 R1-167889 Design of Flexible LDPC Codes
|
|







