|
NR PHY DSP for SSB
In this note, we explore a comprehensive Python-based implementation for detecting and decoding the Physical Broadcast Channel (PBCH) from a 5G NR downlink signal using py3gpp and a SigMF-compliant dataset. The script walks through the entire PBCH decoding pipeline—from loading and preprocessing the raw IQ samples to identifying SSBs, estimating and compensating channel effects, and finally performing polar decoding of the broadcasted system information.
Leveraging 3GPP-compliant signal processing functions through the py3gpp library, this analysis not only demonstrates signal acquisition and demodulation techniques, but also provides deep insights into equalization, noise handling, and decoding performance in realistic radio environments.
NOTE : The source code for this note is available here. The sample IQ file used in this note is avilable at py3gpp. It may look intimidating at the first glance of the code, but large portions of the code is just for debug print. Just removing those debug print, it would not be that different from test_py3gpp.ipynb in py3gpp.
The first stage of the pipeline focuses on loading the downlink signal and preparing it for further processing.
|
#The code begins by reading a SigMF-compliant IQ recording using the following line. This command loads the .sigmf-data file containing the raw complex baseband samples
handle = sigmf.sigmffile.fromfile('30720KSPS_dl_signal.sigmf-data')
# Following this, some initial parameters are defined: These variables allow for configuring the frequency offset (delta_f) and numerology (mu) of the received waveform.
delta_f = 0
f = 1
mu = 0
apply_fine_CFO = 0
# First generate reference sequences
This block doesn't generate all possible reference sequences at once. It creates initial, placeholder versions using default IDs (like NID2=0, NcellID=0). These are used to set up the variables, define their type, and perform initial normalization. The actual detection loops later in the code generate the correct reference sequences on-the-fly (e.g., nrPSS(current_NID2) within the NID2 detection loop) to perform correlations and find the true cell parameters.
The initially generated pssRef, sssRef, and dmrsRef (after normalization) are primarily used later in the script for plotting the "Expected" points on the constellation diagrams, although ideally, they should be regenerated with the detected NID, NID2, and ibar_SSB before plotting for accuracy.
pssRef = nrPSS(0).astype(np.complex128) # Use NID2=0 initially
sssRef = nrSSS(0).astype(np.complex128)
dmrsRef = nrPBCHDMRS(0, ibar_SSB=0).astype(np.complex128)
# Normalize reference sequences to unit power
pssRef = pssRef / np.sqrt(np.mean(np.abs(pssRef)**2))
sssRef = sssRef / np.sqrt(np.mean(np.abs(sssRef)**2))
dmrsRef = dmrsRef / np.sqrt(np.mean(np.abs(dmrsRef)**2))
# Read and preprocess waveform
waveform = handle.read_samples()
waveform /= max(waveform.real.max(), waveform.imag.max()) # scale max amplitude to 1
fs = handle.get_global_field(sigmf.SigMFFile.SAMPLE_RATE_KEY)
waveform = waveform * np.exp(-1j*2*np.pi*delta_f/fs*(np.arange(len(waveform))))
# Normalize waveform to unit power
waveform = waveform / np.sqrt(np.mean(np.abs(waveform)**2))
# Add noise with controlled SNR
if ADD_NOISE:
np.random.seed(NOISE_SEED) # for reproducible noise
# Calculate required noise power for target SNR
signal_power = np.mean(np.abs(waveform)**2)
noise_power = signal_power / (10**(TARGET_SNR_DB/10))
noise_std = np.sqrt(noise_power/2) # Standard deviation for real and imaginary parts
# Generate complex Gaussian noise
noise = (np.random.normal(0, noise_std, waveform.shape[0]) +
1j * np.random.normal(0, noise_std, waveform.shape[0]))
# Add noise to waveform
waveform += noise
# Calculate actual SNR
actual_snr_db = 10 * np.log10(signal_power / np.mean(np.abs(noise)**2))
print(f'Target SNR = {TARGET_SNR_DB} dB')
print(f'Actual SNR = {actual_snr_db:.1f} dB')
|
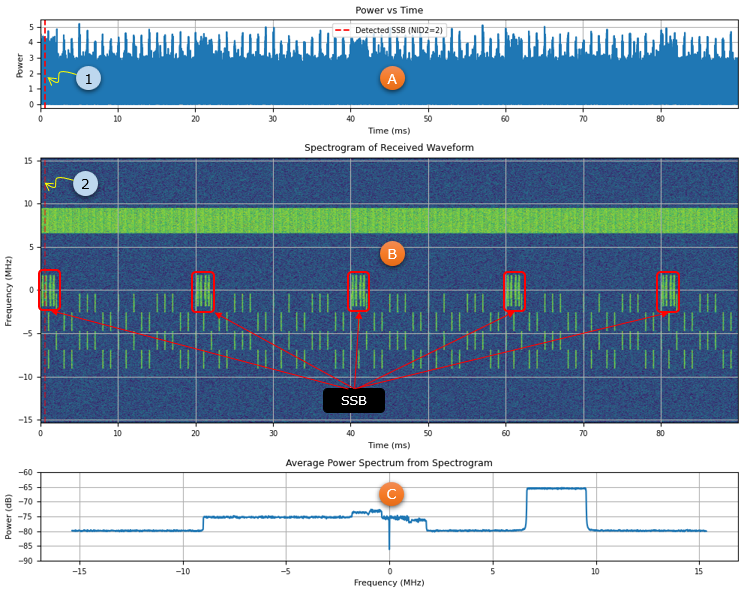
The first step begins with capturing raw IQ samples from a SigMF-formatted downlink recording(a save IQ file), followed by power analysis and SSB detection using correlation with reference waveforms. The visualized output of this step is shown below.
The plot (A) illustrates the time-domain power profile of the received signal, highlighting the moment an SSB burst is detected. The spectrogram (B) offers a detailed time-frequency representation, revealing the periodic structure and spectral occupancy of the waveform. Finally, the plot (C) summarizes the average power spectrum, showing clear frequency bands where signal energy is concentrated. These plots not only validate the integrity of the signal but also provide critical timing
and spectral insights necessary for accurate demodulation and decoding of the PBCH. The red line marked as (1) and (2) indicates the position of SSB by the script in this note.
Preprocessor and Basic Calculation
This code block configures the expected signal structure, then generates each of the three possible PSS signals, correlates them against the received waveform, and identifies which PSS sequence gives the strongest correlation peak, thereby detecting NID2. This is a fundamental first step in synchronizing to a 5G cell
|
# Carrier Configuration
This block configures the fundamental parameters of the 5G New Radio carrier being analyzed. It uses nrCarrierConfig to set the channel bandwidth via NSizeGrid = 106, indicating 106 Physical Resource Blocks (which commonly corresponds to a 20 MHz bandwidth for the typical 15 kHz subcarrier spacing used in synchronization), and defines the SubcarrierSpacing itself, likely set to 15 kHz based on the numerology parameter mu. Subsequently, nrOFDMInfo is used to calculate essential derived
OFDM parameters, such as the appropriate FFT size and cyclic prefix lengths, based on this initial carrier configuration.
carrier = nrCarrierConfig(NSizeGrid = 106, SubcarrierSpacing = 15 * 2**mu)
info = nrOFDMInfo(carrier)
Nfft = info['Nfft']
print(f'Nfft = {Nfft}')
# PSS Preparation and Index Calculation
This section prepares for the Primary Synchronization Signal (PSS) detection by initializing storage arrays (peak_value, peak_index) to hold the results of correlation tests for the three possible NID2 values. It also defines key constants like the PSS length (PSS_LEN) and the number of resource elements per block (NRE_PER_PRB). Crucially, it calculates the precise frequency subcarrier indices (pssIndices) where the PSS signal is expected to be located, centered within the configured
carrier bandwidth.
peak_value = np.zeros(3)
peak_index = np.zeros(3, 'int')
PSS_LEN = 128
NRE_PER_PRB = 12
This calculates the specific frequency indices (subcarrier numbers) where the PSS is located within the full carrier resource grid defined by NSizeGrid. In this case it is assumed that the PSS is centered in the frequency domain. The calculation finds the center subcarrier of the 106 PRBs and then selects the 128 indices centered around it. (NOTE : In 5G, SSB is not always at the center of the resource grid. SSB position in the resource grid is configurable, but it is assumed
to be at the center in this example)
pssIndices = np.arange((carrier.NSizeGrid * NRE_PER_PRB // 2 - PSS_LEN // 2), (carrier.NSizeGrid * NRE_PER_PRB // 2 + PSS_LEN // 2 - 1))
#NID2 Detection Loop (Correlation)/PSS Detection
This block performs the core NID2 detection by systematically testing each of the three possible NID2 values (0, 1, and 2). Within a loop, it generates a candidate time-domain Primary Synchronization Signal (PSS) waveform corresponding to the NID2 value currently being tested. This involves creating the PSS sequence, placing it on a resource grid, performing OFDM modulation, and removing the cyclic prefix. Then, this candidate PSS waveform is cross-correlated with the received signal. The loop finds and stores the magnitude and timing index of the highest correlation peak obtained for each candidate NID2, preparing for the final decision.
for current_NID2 in np.arange(3, dtype='int'):
slotGrid = nrResourceGrid(carrier)
slotGrid = slotGrid[:, 0]
slotGrid[pssIndices] = nrPSS(current_NID2)
[refWaveform, info] = nrOFDMModulate(carrier, slotGrid, SampleRate = fs)
refWaveform = refWaveform[info['CyclicPrefixLengths'][0]:]; # remove CP
temp = scipy.signal.correlate(waveform[:int(25e-3 * fs)], refWaveform, 'valid') # correlate over 25 ms
peak_index[current_NID2] = np.argmax(np.abs(temp))
peak_value[current_NID2] = np.abs(temp[peak_index[current_NID2]])
t_corr = np.arange(temp.shape[0])/fs*1e3
#axs[current_NID2].plot(t_corr, np.abs(temp))
detected_NID2 = np.argmax(peak_value)
Since this part is so important, let me break down the block and look into the detailed meaning
- for current_NID2 in np.arange(3, dtype='int'):: This loop iterates through the three possible values for NID2: 0, 1, and 2.
- slotGrid = nrResourceGrid(carrier): Creates an empty resource grid (frequency vs. time) for one slot, based on the carrier config.
- slotGrid = slotGrid[:, 0]: Simplifies the grid to only consider the first OFDM symbol's frequency resources.
- slotGrid[pssIndices] = nrPSS(current_NID2): Generates the PSS sequence corresponding to the current_NID2 value being tested in this loop iteration and places it onto the calculated frequency pssIndices within the slotGrid.
- [refWaveform, info] = nrOFDMModulate(...): Performs OFDM modulation. It converts the frequency-domain slotGrid (which contains only the PSS for this current_NID2) into a time-domain refWaveform. SampleRate = fs ensures this reference waveform has the same sample rate as the received waveform.
- refWaveform = refWaveform[info['CyclicPrefixLengths'][0]:]: Removes the cyclic prefix (CP) from the beginning of the generated refWaveform. Correlation is usually done using the main part of the OFDM symbol, without the CP.
- temp = scipy.signal.correlate(...): This is the crucial step. It calculates the cross-correlation between a segment of the input waveform (first 25 milliseconds) and the generated refWaveform (the PSS signal for current_NID2). High correlation occurs when the reference PSS aligns well in time with a matching PSS in the received signal.
- peak_index[current_NID2] = np.argmax(np.abs(temp)): Finds the time index where the correlation magnitude (np.abs(temp)) is highest for the current NID2.
- peak_value[current_NID2] = np.abs(temp[peak_index[current_NID2]]): Stores the magnitude of that highest correlation peak.
|
Power vs Time - (A)
This subplot shows the signal's magnitude over time, helping identify when energy bursts like the SSB appear. A vertical red dashed line marks the estimated timing of the detected SSB based on the strongest correlation with the PSS sequence.
|
t_power = np.arange(len(waveform))/fs * 1000 # Time in milliseconds
power_time = np.abs(waveform)
ax0.plot(t_power, power_time)
ssb_time = peak_index[detected_NID2]/fs*1e3 # Convert to milliseconds
ax0.axvline(x=ssb_time, color='r', linestyle='--', label=f'Detected SSB (NID2={detected_NID2})')
|
- power_time = np.abs(waveform) computes the magnitude of the complex waveform.
- t_power represents the time axis in milliseconds.
- ax0.axvline(...) plots the red vertical dashed line to mark the SSB detection time using the peak correlation result: peak_index[detected_NID
Spectrogram of Received Waveform - (B)
This subplot (B) provides a time-frequency view of the received signal using a spectrogram. It reveals periodic SSB bursts and overall spectral activity in the signal. The SSB timing line appears again for reference.
|
nperseg = Nfft
f, t, Sxx = scipy.signal.spectrogram(waveform, fs=fs, nperseg=nperseg, noverlap=noverlap, return_onesided=False)
f = np.fft.fftshift(f)
Sxx = np.fft.fftshift(Sxx, axes=0)
spec = ax1.pcolormesh(t*1000, f/1e6, 10*np.log10(np.abs(Sxx)), shading='gouraud', cmap='viridis', vmin=-90, vmax=-60)
ax1.axvline(x=ssb_time, color='r', linestyle='--', alpha=0.5)
|
- The spectrogram is computed using scipy.signal.spectrogram.
- Frequencies (f) and power values (Sxx) are FFT-shifted to center DC at 0.
- The plotting function ax1.pcolormesh(...) displays the spectrogram in dB scale.
- The red dashed line (ax1.axvline(...)) marks the detected SSB timing, aligned with the time axis.
Average Power Spectrum from Spectrogram - (C)
This bottom subplot shows the average spectral power across time, giving an overall view of signal bandwidth and occupied spectrum.
|
power_spectrum = 10*np.log10(np.mean(np.abs(Sxx), axis=1))
ax2.plot(f/1e6, power_spectrum)
|
- np.mean(np.abs(Sxx), axis=1) averages the spectrogram power over time.
- Converted to dB scale and plotted over frequency using ax2.plot(...).
Detected SSB Position Marker - (1),(2)
The red vertical dashed line (axvline) appears in both the Power vs Time and Spectrogram subplots, helping align the temporal position of the detected SSB across both time and time-frequency views. It is calculated as:
|
ssb_time = peak_index[detected_NID2]/fs*1e3
|
- where peak_index[...] comes from this correlation-based detection loop:
|
temp = scipy.signal.correlate(waveform[:int(25e-3 * fs)], refWaveform, 'valid')
peak_index[current_NID2] = np.argmax(np.abs(temp))
|
- This step identifies the most likely SSB position by matching PSS sequences and detecting the timing offset.
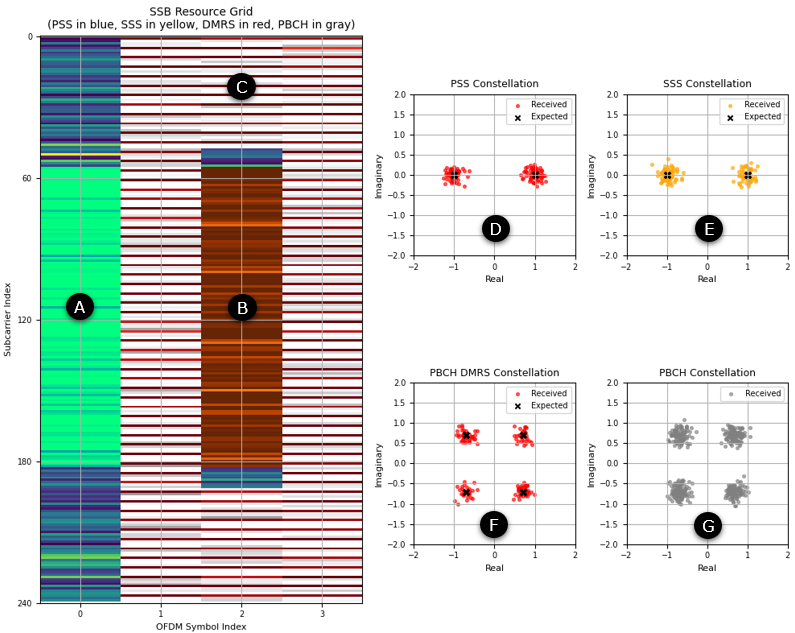
Next step I want to do is to show the grid map of SSB and plot the constellation of each signals and channel in the SSB. The figure shown below presents a detailed view of the 5G NR Synchronization Signal Block (SSB) resource grid, alongside the corresponding constellation diagrams of key downlink signals. The SSB resource grid highlights how individual components—Primary Synchronization Signal (PSS), Secondary Synchronization Signal (SSS), Demodulation Reference Signal (DMRS), and the
Physical Broadcast Channel (PBCH)—are mapped in both frequency and time within the OFDM resource grid. The (A),(B),(C) on the resource grid visualizes these allocations, with color-coded overlays indicating the location of each signal type. The accompanying constellation plots provide a snapshot of the received symbols after extraction, enabling visual assessment of signal quality and modulation accuracy. These plots serve as crucial diagnostics for evaluating synchronization performance and physical layer
decoding robustness under realistic channel conditions. They collectively provide a complete visual diagnosis of the SSB block, from RE allocation to signal demodulation fidelity, helping verify both synchronization and decoding steps in the 5G NR receiver pipeline.
OFDM Demodulation and Resource Grid Preparation
Before any resource extraction or constellation plotting can happen, the raw time-domain waveform must be converted into its corresponding frequency-domain representation, also known as the resource grid. This is where the physical layer structure of 5G NR (like PSS, SSS, PBCH, DMRS) is spatially laid out in terms of subcarriers and OFDM symbols.
Preprocessor and Basic Calculation
This block takes the received waveform and the previously detected NID2, then performs several crucial steps to further synchronize with the 5G cell and prepare for decoding the broadcast channel. It first refines the timing synchronization, then demodulates the relevant part of the signal into a resource grid. Using this grid, it detects the remaining parts of the physical cell ID (NID1, giving the full NID) and the time index of the Synchronization Signal Block (ibar_SSB). Finally, it identifies and extracts the PSS, SSS, PBCH DMRS, and PBCH data symbols from the demodulated grid.
|
# Basic Parameters for SSB
Basic parameters for the SSB are defined: nrbSSB (bandwidth = 20 RBs), scsSSB (subcarrier spacing, likely 15kHz), nSlot (initial slot assumption), and rxSampleRate.
nrbSSB = 20
scsSSB = 15 * 2**(mu)
nSlot = 0
rxSampleRate = fs
# TimingOffset Estimation
This is to find a precise starting point (the timingOffset in samples) within the input waveform that accurately aligns with the beginning of the Synchronization Signal Block (SSB). It does this by utilizing the already detected NID2 to generate the corresponding Primary Synchronization Signal (PSS) and then correlating this known PSS signal against the received waveform to find the point of best match.
refGrid = np.zeros((nrbSSB*12, 2), np.complex128)
refGrid[nrPSSIndices(), 1] = nrPSS(detected_NID2)
timingOffset = nrTimingEstimate(waveform = waveform, nrb = nrbSSB, scs = scsSSB, initialNSlot = nSlot, refGrid = refGrid, SampleRate = rxSampleRate)
Following is the break down of the block
- refGrid = np.zeros((nrbSSB*12, 2), np.complex128): Creates a small, empty resource grid. It spans the SSB bandwidth (20 RBs * 12 subcarriers/RB = 240 subcarriers) and covers 2 OFDM symbols.
- refGrid[nrPSSIndices(), 1] = nrPSS(detected_NID2): This line generates the PSS sequence based on the previously found detected_NID2. It then places this PSS sequence onto the appropriate subcarriers (nrPSSIndices()) within the first symbol (index 1) of the refGrid. This creates a reference signal containing just the PSS in its expected symbol position within the SSB structure.
- timingOffset = nrTimingEstimate(...): This function performs the core timing estimation.
- It takes the waveform, SSB parameters (nrb, scs, SampleRate), slot context (initialNSlot), and importantly, the refGrid containing only the PSS as inputs.
- The function likely works by correlating the reference PSS (from refGrid) against the time-domain waveform to find the time index where the correlation peak occurs, indicating the start of the SSB.
- The resulting sample index is stored in the timingOffset variable, which will be used subsequently for OFDM demodulation.
# modulate about 8 symbols, only has to be at least 5
This block first takes the time-synchronized input signal (waveform starting at timingOffset) and converts a portion of it, guaranteed to contain the Synchronization Signal Block (SSB), from the time domain into its frequency domain representation (a resource grid). It then precisely extracts the specific 4 OFDM symbols that make up the SSB from this grid, preparing them for further analysis like signal extraction and decoding.
rxGrid = nrOFDMDemodulate(waveform = waveform[timingOffset:][:np.min((len(waveform), 2048*8))], nrb = nrbSSB, scs = scsSSB, initialNSlot = nSlot, SampleRate=rxSampleRate, CyclicPrefixFraction=0.5)
rxGrid = rxGrid[:,1:5]
Following is the breakdown of the code
- rxGrid = nrOFDMDemodulate(...): This function performs the OFDM demodulation.
- It processes a segment of the waveform starting at the calculated timingOffset and extending for roughly 8 symbol durations (2048*8 samples, adjusted if the waveform ends sooner).
- It uses parameters specific to the SSB (nrbSSB, scsSSB, rxSampleRate) to correctly interpret the signal structure.
- The output rxGrid is a 2D array containing the complex values for each subcarrier (rows) across the demodulated OFDM symbols (columns, approx. 8 of them).
- rxGrid = rxGrid[:, 1:5]: This line uses NumPy slicing to select a specific portion of the rxGrid.
- : selects all rows (all 240 subcarriers for nrbSSB=20).
- 1:5 selects the columns (OFDM symbols) with indices 1, 2, 3, and 4.
- This precisely isolates the 4 OFDM symbols that constitute the SSB according to the 5G standard, discarding any extra symbols demodulated before (index 0) or after (indices 5, 6, 7).
- The rxGrid variable is updated to hold only these 4 relevant symbols.
# Normalize by FFT size and additional factor to get correct constellation scaling
This line scales the amplitude of all the complex values within the demodulated rxGrid. The main goal is to adjust the overall power level so that the received signal constellation points (PSS, SSS, DMRS, PBCH) align correctly with their expected standard positions, typically having magnitudes around 1, which simplifies visualization and subsequent processing steps like channel estimation or symbol demodulation.
rxGrid = rxGrid / (np.sqrt(Nfft) * 3.0) # Factor of 3 to match expected constellation points
- rxGrid = rxGrid / ...: This performs element-wise division on the entire rxGrid array. Every complex value in the grid is divided by the calculated normalization factor.
- np.sqrt(Nfft): This part applies standard OFDM normalization. The process of OFDM demodulation (which involves an FFT) introduces a scaling factor related to the FFT size (Nfft, likely 2048 in this context). Dividing by the square root of Nfft compensates for this inherent scaling introduced by the FFT operation.
- * 3.0: This is an additional, empirical, scaling factor.
- its purpose: to further adjust the scale so the received symbols visually match the ideal constellation points (e.g., QPSK points at +1/-1 on real/imag axes, or normalized to unit magnitude).
# Get SSS indices and convert to frequency indices
This block focuses on isolating the Secondary Synchronization Signal (SSS) from the demodulated SSB resource grid (rxGrid). It first identifies the specific resource elements where the SSS is located, extracts the corresponding received complex symbols, and then applies a specific normalization to these symbols, likely to prepare them for the correlation process used to detect NID1.
sssIndices = nrSSSIndices()
sssRx = nrExtractResources(sssIndices, rxGrid)
sssRx /= np.max((sssRx.real.max(), sssRx.imag.max())) # scale sssRx symbols individually
- sssIndices = nrSSSIndices(): This function returns a list or array of standardized indices representing the specific time-frequency locations (resource elements) within the 4-symbol SSB grid where the SSS is transmitted. The SSS resides in the 3rd symbol (index 2) of the SSB.
- sssRx = nrExtractResources(sssIndices, rxGrid): This function uses the sssIndices to look up and extract the complex values from the rxGrid (which contains the 4 SSB symbols). The result, sssRx, is a vector containing the received symbols specifically for the SSS.
- sssRx /= np.max((sssRx.real.max(), sssRx.imag.max())): This line performs a specific normalization on the extracted sssRx symbols:
- It finds the maximum value among all real parts and the maximum value among all imaginary parts of the sssRx symbols.
- It takes the larger of these two maximums (i.e., the maximum extent of the constellation along either the real or imaginary axis).
- It divides every symbol in sssRx by this single maximum value.
- The effect is to scale the received SSS constellation so that the point furthest from the origin along either the real or imaginary axis now touches +1 on that axis (assuming the maximum value was positive). This type of normalization aims to adjust the overall amplitude scale before correlation, making it less sensitive to gain variations, while using the peak value as the reference.
# SSS correlation for NID1 detection
This section identifies the remaining component (NID1) needed to determine the full Physical Cell ID (NcellID) of the 5G cell. It achieves this by comparing the received Secondary Synchronization Signal (SSS) symbols, extracted previously (sssRx), against every possible reference SSS sequence. The reference sequence that best matches the received SSS reveals the correct NID1, which is then combined with the already known NID2 to get the full NcellID.
sssEst = np.zeros(336)
for NID1 in range(335):
ncellid = (3*NID1) + detected_NID2
sssRef = nrSSS(ncellid)
sssEst[NID1] = np.abs(np.vdot(sssRx, sssRef))
detected_NID1 = np.argmax(sssEst)
detected_NID = detected_NID1*3 + detected_NID2
- sssEst = np.zeros(336): An array named sssEst is initialized with zeros. It has a size of 336 to store the correlation results for each possible NID1 hypothesis (where NID1 ranges from 0 to 335).
- for NID1 in range(335):: This loop iterates through potential NID1 values. Note: range(335) generates values from 0 up to 334. If the full range of NID1 (0-335) needs to be tested, this loop should ideally be range(336). As written, it tests NID1 from 0 to 334.
- ncellid = (3*NID1) + detected_NID2: Inside the loop, this line calculates a candidate full Physical Cell ID (ncellid) based on the current NID1 being tested and the detected_NID2 found earlier. This follows the standard 5G formula: NcellID = 3 * NID1 + NID2.
- sssRef = nrSSS(ncellid): This generates the theoretical reference SSS sequence that corresponds to the candidate ncellid. Each NcellID (0-1007) has a unique SSS sequence.
- sssEst[NID1] = np.abs(np.vdot(sssRx, sssRef)): This is the core correlation step:
- np.vdot(sssRx, sssRef) computes the complex dot product between the received SSS symbols (sssRx) and the reference SSS sequence (sssRef). This measures how well they match.
- np.abs(...) takes the magnitude of the complex correlation result. A higher magnitude signifies a stronger match.
- The result is stored in the sssEst array at the index corresponding to the current NID1.
- detected_NID1 = np.argmax(sssEst): After the loop finishes testing all the NID1 hypotheses (0-334 in this case), this finds the index in sssEst that has the largest value. This index represents the most likely NID1.
- detected_NID = detected_NID1*3 + detected_NID2: This final calculation combines the detected_NID1 with the previously known detected_NID2 using the standard formula to determine the overall detected Physical Cell ID (detected_NID).
# DMRS correlation for ibar_SSB detection
This section determines the specific time index (ibar_SSB) of the received Synchronization Signal Block (SSB) relative to other potential SSBs within a burst. It works by comparing the received Demodulation Reference Signal (DMRS) symbols associated with the Physical Broadcast Channel (PBCH) against reference DMRS sequences generated for different possible ibar_SSB values. The ibar_SSB value whose reference DMRS best matches the received DMRS reveals the index of the received SSB, which is essential information for later PBCH decoding steps (specifically descrambling).
dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab')
xcorrPBCHDMRS = np.empty(7)
for ibar_SSB in range(7):
PBCHDMRS = nrPBCHDMRS(detected_NID, ibar_SSB)
xcorrPBCHDMRS[ibar_SSB] = np.abs(np.vdot(nrExtractResources(dmrsIndices, rxGrid), PBCHDMRS))
ibar_SSB = np.argmax(np.abs(xcorrPBCHDMRS))
Following is the breakdown of the code and description
- dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab'): This function call retrieves the specific resource element indices within the 4-symbol SSB grid where the PBCH DMRS symbols are located. The DMRS pattern depends on the Physical Cell ID (detected_NID). The style='matlab' argument likely ensures the indices follow a specific convention (e.g., 1-based or ordering) compatible with MATLAB implementations.
- xcorrPBCHDMRS = np.empty(7): Initializes an empty NumPy array intended to store the correlation results for the 7 different ibar_SSB hypotheses being tested (indices 0 through 6).
- for ibar_SSB in range(7):: This loop iterates through the ibar_SSB hypotheses, testing the values 0, 1, 2, 3, 4, 5, and 6. Note: The actual maximum value of ibar_SSB (Lmax) can vary (4, 8, or 64 depending on frequency band), but the scrambling sequence used for PBCH often depends on ibar_SSB mod 8. Testing 0-6 covers a significant range of possibilities.
- PBCHDMRS = nrPBCHDMRS(detected_NID, ibar_SSB): Inside the loop, this generates the reference PBCH DMRS sequence for the current ibar_SSB hypothesis. The sequence itself depends on NID, and its scrambling depends on ibar_SSB.
- xcorrPBCHDMRS[ibar_SSB] = np.abs(np.vdot(nrExtractResources(dmrsIndices, rxGrid), PBCHDMRS)): This performs the correlation:
- nrExtractResources(dmrsIndices, rxGrid): Extracts the received DMRS symbols from the rxGrid at the locations specified by dmrsIndices.
- np.vdot(...): Calculates the complex dot product (correlation) between the extracted received DMRS and the generated reference DMRS (PBCHDMRS).
- np.abs(...): Takes the magnitude of the correlation result.
- The magnitude is stored in the xcorrPBCHDMRS array at the index corresponding to the current ibar_SSB hypothesis.
- ibar_SSB = np.argmax(np.abs(xcorrPBCHDMRS)): After testing hypotheses 0 through 6, this line finds the index (0-6) that yielded the highest correlation magnitude in the xcorrPBCHDMRS array. This index is then assigned to the ibar_SSB variable, representing the detected time index of the received SSB among the tested possibilities.
# Create masks for PSS and SSS
This section initializes several boolean arrays (masks) that have the same dimensions as the rxGrid (which holds the 4 symbols of the SSB). These masks (pss_mask, sss_mask, dmrs_mask, pbch_mask) act like templates, initially all set to False. They will be used in the following steps to mark the specific locations (resource elements) within the rxGrid where each type of signal (PSS, SSS, DMRS, PBCH) resides.
pss_mask = np.zeros_like(rxGrid, dtype=bool)
sss_mask = np.zeros_like(rxGrid, dtype=bool)
dmrs_mask = np.zeros_like(rxGrid, dtype=bool)
pbch_mask = np.zeros_like(rxGrid, dtype=bool)
Following is the breakdown of the code and description
- pss_mask = np.zeros_like(rxGrid, dtype=bool): Creates a NumPy array pss_mask having the identical shape as rxGrid. The dtype=bool ensures it contains boolean values, and zeros_like initializes all elements to False. This mask will later identify PSS resource elements.
- sss_mask = np.zeros_like(rxGrid, dtype=bool): Similarly, creates sss_mask, a boolean array of the same shape as rxGrid, initialized to all False, intended for marking SSS locations.
- dmrs_mask = np.zeros_like(rxGrid, dtype=bool): Creates dmrs_mask, another boolean array matching rxGrid's shape, initialized to all False, intended for marking PBCH DMRS locations.
- pbch_mask = np.zeros_like(rxGrid, dtype=bool): Creates pbch_mask, a final boolean array matching rxGrid's shape, initialized to all False, intended for marking PBCH data symbol locations.
# Get PSS indices for SSB grid
This block determines the exact frequency locations (subcarrier indices) occupied by the Primary Synchronization Signal (PSS) within the SSB's bandwidth. It then updates the pss_mask (created in the previous step) by marking these specific frequency locations within the first symbol of the SSB grid as True.
pssIndices = nrPSSIndices()
pss_freq_indices = pssIndices % (nrbSSB * 12) # Convert to frequency indices for SSB grid
pss_mask[pss_freq_indices, 0] = True # PSS is in first symbol
Following is the breakdown of the code and description
- pssIndices = nrPSSIndices(): This function retrieves the standard resource element indices where the PSS resides. These indices define which specific subcarriers (out of the 240 within the SSB's 20 Resource Blocks) carry the PSS signal.
- pss_freq_indices = pssIndices % (nrbSSB * 12): This line ensures the indices are mapped correctly within the frequency dimension of the rxGrid.
- nrbSSB * 12 calculates the total number of subcarriers in the SSB bandwidth (20 * 12 = 240).
- The modulo operator (%) effectively maps the pssIndices (if they weren't already 0-based relative to the SSB) into the range 0-239, representing the frequency index within the rxGrid. The result is stored in pss_freq_indices.
- pss_mask[pss_freq_indices, 0] = True: This command modifies the pss_mask.
- It uses pss_freq_indices to select the rows (subcarriers) corresponding to the PSS.
- It uses 0 to select the first column (OFDM symbol with index 0) within the 4-symbol mask, as the PSS occurs in the first symbol of the SSB structure.
- It sets the value at these specific row/column intersections within the pss_mask to True, marking the location of the PSS.
# Get SSS indices for SSB grid
Similar to the PSS masking, this code block determines the specific frequency locations (subcarrier indices) used by the Secondary Synchronization Signal (SSS) within the SSB's bandwidth. It then updates the sss_mask by marking these frequency locations within the third symbol (index 2) of the SSB grid as True.
sss_freq_indices = sssIndices % (nrbSSB * 12) # Convert to frequency indices for SSB grid
sss_mask[sss_freq_indices, 2] = True # SSS is in third symbol (index 2)
Following is the breakdown of the code and description
- sss_freq_indices = sssIndices % (nrbSSB * 12): This calculates the frequency indices for the SSS within the 0-239 subcarrier range of the SSB grid.
- sssIndices: This variable (presumably defined earlier, e.g., by sssIndices = nrSSSIndices()) contains the standard resource element indices for the SSS.
- nrbSSB * 12: Calculates the total number of subcarriers (240) within the SSB bandwidth.
- The modulo operator (%) maps the sssIndices into the range 0-239, corresponding to the frequency dimension (rows) of the rxGrid and masks. The result is stored in sss_freq_indices.
- sss_mask[sss_freq_indices, 2] = True: This command modifies the sss_mask.
- It uses sss_freq_indices to select the rows (subcarriers) where the SSS is located.
- It uses 2 to select the third column (OFDM symbol with index 2) within the 4-symbol mask. This is because the SSS is transmitted in the third symbol of the standard SSB structure.
- It sets the value at these specific SSS locations (rows specified by sss_freq_indices, column 2) within the sss_mask to True.
# Get PBCH DMRS indices
This block identifies the precise time-frequency locations (resource elements) within the 4-symbol SSB grid (rxGrid) where the PBCH DMRS is transmitted. It calculates the specific subcarrier and OFDM symbol indices for every DMRS symbol based on the detected Physical Cell ID (detected_NID) and then marks these locations as True in the dmrs_mask.
dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab')
symbol_size = nrbSSB * 12
symbol_indices = dmrsIndices // symbol_size # Get symbol indices
freq_indices = dmrsIndices % symbol_size # Get frequency indices
for i in range(len(freq_indices)):
dmrs_mask[freq_indices[i], symbol_indices[i]] = True
Following is the breakdown of the code and description
- dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab'): This function call retrieves the standard indices for the PBCH DMRS resource elements. The locations of these DMRS symbols depend on the detected_NID. The function likely returns these as linear indices (e.g., 0 to 959 for a 240x4 grid) relative to the start of the SSB grid. The style='matlab' argument likely specifies a particular indexing convention.
- symbol_size = nrbSSB * 12: Calculates the number of subcarriers within one OFDM symbol of the SSB (20 RBs * 12 subcarriers/RB = 240). This value represents the size of the frequency dimension.
- symbol_indices = dmrsIndices // symbol_size: This performs integer division of the linear dmrsIndices by the symbol_size. This effectively converts the linear index into the corresponding OFDM symbol index (0, 1, 2, or 3) within the 4-symbol SSB structure.
- freq_indices = dmrsIndices % symbol_size: This calculates the modulo (remainder) of the linear dmrsIndices divided by the symbol_size. This remainder gives the corresponding frequency index (subcarrier index, ranging from 0 to 239) within that OFDM symbol.
- for i in range(len(freq_indices)):: This loop iterates through all the calculated DMRS indices (the number of DMRS symbols within the SSB).
- dmrs_mask[freq_indices[i], symbol_indices[i]] = True: Inside the loop, for each DMRS symbol (i), this line takes its calculated frequency index (freq_indices[i]) and symbol index (symbol_indices[i]) and sets the corresponding element in the dmrs_mask to True. After the loop completes, all PBCH DMRS locations are marked True in the dmrs_mask.
# Get PBCH indices
This code identifies all the potential time-frequency locations (resource elements) within the 4-symbol SSB grid (rxGrid) that are designated for carrying the actual Physical Broadcast Channel (PBCH) data. It calculates the specific subcarrier and OFDM symbol index for each of these potential PBCH locations based on the detected Physical Cell ID (detected_NID) and marks these positions as True in the pbch_mask. Note that this initial marking includes resource elements that are also used for DMRS.
pbchIndices = nrPBCHIndices(detected_NID)
pbch_symbol_indices = pbchIndices // symbol_size
pbch_freq_indices = pbchIndices % symbol_size
for i in range(len(pbch_freq_indices)):
pbch_mask[pbch_freq_indices[i], pbch_symbol_indices[i]] = True
Following is the breakdown of the code and description
- pbchIndices = nrPBCHIndices(detected_NID): This function call retrieves the standard indices for all resource elements allocated to the PBCH (data and potential DMRS overlaps). The specific locations depend on the detected_NID. These are likely returned as linear indices (e.g., 0-959) relative to the start of the 240x4 SSB grid.
- pbch_symbol_indices = pbchIndices // symbol_size: Calculates the OFDM symbol index (0, 1, 2, or 3) for each PBCH resource element index by performing integer division of the linear pbchIndices by symbol_size (which is 240, the number of subcarriers per symbol). PBCH data primarily resides in symbols 1 and 3 of the SSB.
- pbch_freq_indices = pbchIndices % symbol_size: Calculates the frequency index (subcarrier index, 0-239) for each PBCH resource element index by taking the modulo of the linear pbchIndices with symbol_size (240).
- for i in range(len(pbch_freq_indices)):: This loop iterates through all the resource element indices allocated for the PBCH.
- pbch_mask[pbch_freq_indices[i], pbch_symbol_indices[i]] = True: Inside the loop, for each PBCH location (i), it uses the calculated frequency index (pbch_freq_indices[i]) and symbol index (pbch_symbol_indices[i]) to set the corresponding element in the pbch_mask to True. This marks all potential PBCH locations, including those that will later be identified as DMRS-only.
# Remove DMRS positions from PBCH mask to avoid overlap
This line performs a logical operation to refine the pbch_mask. Its purpose is to ensure that the final pbch_mask only identifies the resource elements carrying actual PBCH data, by explicitly removing any locations that are occupied by the PBCH DMRS.
pbch_mask = pbch_mask & ~dmrs_mask
Following is the breakdown of the code and description
- pbch_mask = pbch_mask & ~dmrs_mask: This performs an element-wise logical AND operation between two boolean masks:
- pbch_mask: At this point, it contains True for all resource elements designated for PBCH (including potential overlaps with DMRS).
- dmrs_mask: Contains True only at the locations of DMRS symbols.
- ~dmrs_mask: The ~ (tilde) is a logical NOT operator. It inverts dmrs_mask, resulting in a mask that is True everywhere except at the DMRS locations, where it is False.
- &: The logical AND operator compares pbch_mask and ~dmrs_mask element by element. The result for each element is True only if the element is True in both masks.
- If an element was True in the original pbch_mask (part of PBCH allocation) AND True in ~dmrs_mask (meaning it's not a DMRS location), the result is True.
- If an element was True in the original pbch_mask BUT False in ~dmrs_mask (meaning it is a DMRS location), the result is False.
- Result: The pbch_mask is updated so that it now contains True only for the resource elements carrying PBCH data symbols, excluding those used for DMRS pilots.
# Extract received signals
This block extracts the actual received complex symbols for the Primary Synchronization Signal (PSS), Secondary Synchronization Signal (SSS), and the PBCH Demodulation Reference Signal (DMRS) from the main rxGrid. It uses the specific frequency and symbol indices determined in previous steps to pinpoint these signals within the 4-symbol SSB grid structure. The resulting arrays (pssRx, sssRx, dmrsRx) contain the demodulated values for each respective signal.
pssRx = rxGrid[pss_freq_indices, 0]
sssRx = rxGrid[sss_freq_indices, 2]
dmrsRx = rxGrid[freq_indices, symbol_indices]
Following is the breakdown of the code and description
- pssRx = rxGrid[pss_freq_indices, 0]:
- Extracts the PSS symbols.
- It indexes the rxGrid using:
- pss_freq_indices: An array holding the subcarrier indices for the PSS.
- 0: The index for the first OFDM symbol (where PSS is located).
- The resulting 1D array pssRx contains the complex values received at the PSS locations.
- sssRx = rxGrid[sss_freq_indices, 2]:
- Extracts the SSS symbols.
- It indexes the rxGrid using:
- sss_freq_indices: An array holding the subcarrier indices for the SSS.
- 2: The index for the third OFDM symbol (where SSS is located).
- The resulting 1D array sssRx contains the complex values received at the SSS locations. Note: This likely overwrites the previously normalized sssRx used for detection, now storing the values directly from the scaled rxGrid.
- dmrsRx = rxGrid[freq_indices, symbol_indices]:
- Extracts the PBCH DMRS symbols using advanced NumPy indexing.
- freq_indices: An array containing the subcarrier index for each DMRS symbol.
- symbol_indices: An array (same length as freq_indices) containing the OFDM symbol index for each corresponding DMRS symbol.
- NumPy uses these paired arrays to pick out the complex values from rxGrid at each specified (frequency, symbol) coordinate corresponding to a DMRS symbol.
- The resulting 1D array dmrsRx holds the complex values received at the PBCH DMRS locations.
# Extract PBCH signals (excluding DMRS positions)
This block carefully extracts the received complex symbols that correspond only to the actual Physical Broadcast Channel (PBCH) data, explicitly excluding the symbols used for the PBCH DMRS (Demodulation Reference Signal). It achieves this by iterating through the list of all potential PBCH resource element locations but only selecting those that are marked as True in the refined pbch_mask (where DMRS locations have already been set to False). The complex symbols from these validated PBCH data locations are then gathered from the rxGrid into the pbchRx array.
pbch_freq_indices_no_dmrs = []
pbch_symbol_indices_no_dmrs = []
for i in range(len(pbch_freq_indices)):
if pbch_mask[pbch_freq_indices[i], pbch_symbol_indices[i]]: # Only include if not overlapping with DMRS
pbch_freq_indices_no_dmrs.append(pbch_freq_indices[i])
pbch_symbol_indices_no_dmrs.append(pbch_symbol_indices[i])
pbchRx = rxGrid[pbch_freq_indices_no_dmrs, pbch_symbol_indices_no_dmrs]
Following is the breakdown of the code and description
- pbch_freq_indices_no_dmrs = []: Initializes an empty list to collect the frequency indices (subcarrier numbers) of the resource elements carrying only PBCH data.
- pbch_symbol_indices_no_dmrs = []: Initializes a corresponding empty list to collect the OFDM symbol indices for those PBCH data resource elements.
- for i in range(len(pbch_freq_indices)):: This loop iterates through all the indices (pbch_freq_indices and pbch_symbol_indices) that were initially determined as potential PBCH locations (before DMRS removal).
- if pbch_mask[pbch_freq_indices[i], pbch_symbol_indices[i]]:: Inside the loop, this condition checks the value within the refined pbch_mask at the specific location defined by the current frequency index (pbch_freq_indices[i]) and symbol index (pbch_symbol_indices[i]).
- Since pbch_mask was previously updated to be False at DMRS locations (via pbch_mask & ~dmrs_mask), this condition will only be True if the current location is not a DMRS location, meaning it contains actual PBCH data.
- pbch_freq_indices_no_dmrs.append(pbch_freq_indices[i]): If the if condition is met (the location is confirmed to be PBCH data only), the current frequency index is added to the pbch_freq_indices_no_dmrs list.
- pbch_symbol_indices_no_dmrs.append(pbch_symbol_indices[i]): Similarly, the corresponding symbol index is added to the pbch_symbol_indices_no_dmrs list.
- pbchRx = rxGrid[pbch_freq_indices_no_dmrs, pbch_symbol_indices_no_dmrs]: After the loop has filtered all the indices, this line uses advanced NumPy indexing. It takes the lists of validated frequency and symbol indices (pbch_freq_indices_no_dmrs, pbch_symbol_indices_no_dmrs) and uses them to extract the corresponding complex values directly from the rxGrid.
- The final 1D array pbchRx contains only the received complex symbols for the PBCH data, ready for the next processing stages like equalization and decoding.
|
OFDM Demodulation
This block performs OFDM demodulation on a portion of the received time-domain signal (waveform). It essentially transforms the signal from the time domain back into the frequency domain, organizing it into a resource grid (rxGrid) where each element represents the complex value on a specific subcarrier during a specific OFDM symbol. This step is necessary to access the synchronization signals (like PSS, SSS) and the broadcast channel (PBCH) which are transmitted on specific resource elements within this grid structure.
|
rxGrid = nrOFDMDemodulate(
waveform = waveform[timingOffset:][:np.min((len(waveform), 2048*8))],
nrb = nrbSSB,
scs = scsSSB,
initialNSlot = nSlot,
SampleRate = rxSampleRate,
CyclicPrefixFraction = 0.5
)
|
- rxGrid = nrOFDMDemodulate(...): This function call executes the OFDM demodulation process.
- waveform = waveform[timingOffset:][:np.min((len(waveform), 2048*8))]: This selects the specific segment of the input time-domain waveform to be demodulated.
- waveform[timingOffset:]: It starts processing the waveform from the timingOffset, which was likely calculated previously (e.g., via PSS correlation) to align with the beginning of the Synchronization Signal Block (SSB).
- [:np.min((len(waveform), 2048*8))]: It takes a limited number of samples from the offset point – enough to cover approximately 8 OFDM symbols (assuming an FFT size Nfft=2048, common for a 20 MHz channel), but not exceeding the remaining length of the waveform. This duration is sufficient to contain the 4 symbols of the SSB.
- nrb = nrbSSB: Specifies the bandwidth for demodulation in terms of the number of resource blocks. nrbSSB is typically 20, corresponding to the standard bandwidth of an SSB.
- scs = scsSSB: Defines the subcarrier spacing (e.g., 15 kHz or 30 kHz) associated with the SSB being demodulated.
- initialNSlot = nSlot: Indicates the starting slot number context for the demodulation.
- SampleRate = rxSampleRate: Provides the sample rate of the input waveform, which is essential for the demodulator's internal calculations (like FFT windowing and symbol timing).
- CyclicPrefixFraction = 0.5: This parameter likely relates to how the function handles the removal of the cyclic prefix, possibly defining a search window or an assumed fractional starting point for the useful part of the symbol, helping to cope with minor timing errors.
Symbol Range Selection
-
This selects OFDM symbols 1 through 4, which correspond to the active portion of the SSB.
-
SSB elements like PSS, SSS, DMRS, and PBCH all reside in these symbols.
Grid Normalization
|
rxGrid = rxGrid / (np.sqrt(Nfft) * 3.0)
|
-
The grid is normalized by the FFT size to correct for energy scaling.
-
The extra factor of 3.0 is empirically chosen to match the expected constellation amplitude (e.g., QPSK at ±1/√2).
-
Without this, constellation diagrams would appear incorrectly scaled and may affect demodulation accuracy.
SSB Resource Grid - Background Layer
This section visualizes the background layer of the SSB resource grid by plotting the magnitude of received elements that are not part of PSS, SSS, DMRS, or PBCH. It uses the rxGrid, which is the demodulated frequency-domain grid, and applies a viridis colormap to highlight only the non-overlapping resource elements. The np.where condition filters out all known signal positions, allowing the viewer to focus on unused or residual areas within the grid structure.
|
ssb_data = np.abs(rxGrid)
plt.imshow(np.where(~(pss_mask | sss_mask | dmrs_mask | pbch_mask), ssb_data, np.nan),
aspect='auto', interpolation='none', cmap='viridis')
|
- rxGrid is the demodulated resource grid extracted from the waveform.
- ssb_data contains the magnitudes of the received resource elements.
- The background layer shows all non-occupied (non-PSS, non-SSS, non-DMRS, non-PBCH) REs in the grid using a viridis colormap.
- np.where(...) ensures only non-overlapping REs are shown in this layer.
PBCH Layer in the Grid
This part of the visualization overlays the PBCH (Physical Broadcast Channel) resource elements on the SSB grid using a gray colormap. The pbch_mask identifies where PBCH symbols are located within the grid, and these values are displayed on top of the existing background layer. The corresponding amplitudes from ssb_data are rendered only at the positions marked by the mask, allowing a clear distinction of the PBCH structure within the overall resource allocation.
|
plt.imshow(np.where(pbch_mask, ssb_data, np.nan), aspect='auto', interpolation='none',
cmap='gray', vmin=0, vmax=1)
|
- This overlay highlights PBCH REs using a gray colormap.
- pbch_mask is a boolean mask identifying the PBCH RE positions.
- These are rendered on top of the background layer with their respective signal amplitudes.
DMRS, PSS, SSS Layers in the Grid
This section overlays the positions of DMRS, PSS, and SSS onto the SSB resource grid using color-coded layers. The DMRS elements are shown in red, PSS in blue (using the 'winter' colormap), and SSS in yellow-orange (using 'YlOrBr'), each identified by their respective boolean masks. These overlays are rendered on top of the background grid, allowing clear visual differentiation of the individual reference signal components. The np.where condition ensures that only the relevant resource elements
for each signal type are displayed, effectively isolating their structure within the overall grid.
|
plt.imshow(np.where(dmrs_mask, ssb_data, np.nan), aspect='auto', interpolation='none',
cmap='Reds', vmin=0, vmax=1)
plt.imshow(np.where(pss_mask, ssb_data, np.nan), aspect='auto', interpolation='none',
cmap='winter', vmin=0, vmax=1)
plt.imshow(np.where(sss_mask, ssb_data, np.nan), aspect='auto', interpolation='none',
cmap='YlOrBr', vmin=0, vmax=1)
|
- These lines add overlay layers for each reference signal:
- DMRS in red,
- PSS marked as (A),
- SSS marked as (C)
- The masks (*_mask) define RE positions, and np.where filters out irrelevant points.
PSS Constellation - (D)
This plot visualizes the constellation of the Primary Synchronization Signal (PSS) by comparing the received symbols to the expected reference sequence. The variable pssRx holds the complex-valued received PSS samples extracted from the demodulated resource grid, while pssRef contains the locally generated reference PSS sequence. Using a scatter plot, the received symbols are plotted in red and semi-transparent, while the ideal constellation points are marked in black with 'x' markers. This
allows for a direct visual assessment of how accurately the receiver captured the PSS under current channel conditions.
|
plt.scatter(pssRx.real, pssRx.imag, c='red', alpha=0.6, s=30, marker='.', label='Received')
plt.scatter(pssRef.real, pssRef.imag, c='black', s=20, marker='x', label='Expected')
|
- pssRx contains the received PSS samples extracted from rxGrid.
- pssRef is the locally generated reference sequence.
- This scatter plot compares the received PSS constellation to the ideal one.
SSS Constellation - (E)
This subplot displays the Secondary Synchronization Signal (SSS) constellation, comparing the received and reference symbols. The variable sssRx contains the SSS samples extracted from the demodulated grid, while sssRef holds the ideal SSS sequence generated based on the detected cell ID. The plot uses orange dots to show the received symbols and black 'x' markers to indicate the expected positions. By comparing the two, one can assess how accurately the receiver has captured and demodulated
the SSS in the presence of noise and channel distortion.
|
plt.scatter(sssRx.real, sssRx.imag, c='orange', alpha=0.6, s=30, marker='.', label='Received')
plt.scatter(sssRef.real, sssRef.imag, c='black', s=20, marker='x', label='Expected')
|
- sssRx is the extracted SSS from the grid.
- sssRef is the corresponding reference.
- This plot visualizes how closely the received SSS matches the expected constellation.
PBCH DMRS Constellation - (F)
This plot illustrates the PBCH DMRS (Demodulation Reference Signal) constellation, comparing received symbols to their expected values. The dmrsRx array holds the DMRS samples extracted from the resource grid using predefined DMRS indices, while dmrsRef contains the corresponding ideal sequence generated based on the detected NID and ibar_SSB. The received points are plotted in red, and the reference points are shown in black with 'x' markers. This comparison is crucial for evaluating the quality
of the channel and the accuracy of the channel estimation used later during PBCH equalization.
|
plt.scatter(dmrsRx.real, dmrsRx.imag, c='red', alpha=0.6, s=30, marker='.', label='Received')
plt.scatter(dmrsRef.real, dmrsRef.imag, c='black', s=20, marker='x', label='Expected')
|
- dmrsRx includes the received DMRS samples extracted using the known DMRS indices.
- dmrsRef is generated based on the detected NID and ibar_SSB.
- Comparing these helps assess channel quality and estimation performance
PBCH Constellation - (G)
This constellation plot shows the received PBCH symbols after excluding the DMRS positions. The data points in pbchRx are plotted in gray, representing the raw QPSK-modulated PBCH values as captured from the resource grid. No reference symbols are plotted in this case, since the transmitted PBCH content depends on encoded system information bits, which vary between transmissions. The plot provides a visual impression of modulation quality and potential impairments affecting the PBCH without
making assumptions about the encoded data.
|
plt.scatter(pbchRx.real, pbchRx.imag, c='gray', alpha=0.6, s=30, marker='.', label='Received')
|
- pbchRx contains the received PBCH samples (excluding DMRS REs).
- Only the received points are plotted here (no reference overlay), since QPSK-modulated PBCH symbols vary depending on the encoded system info bits.
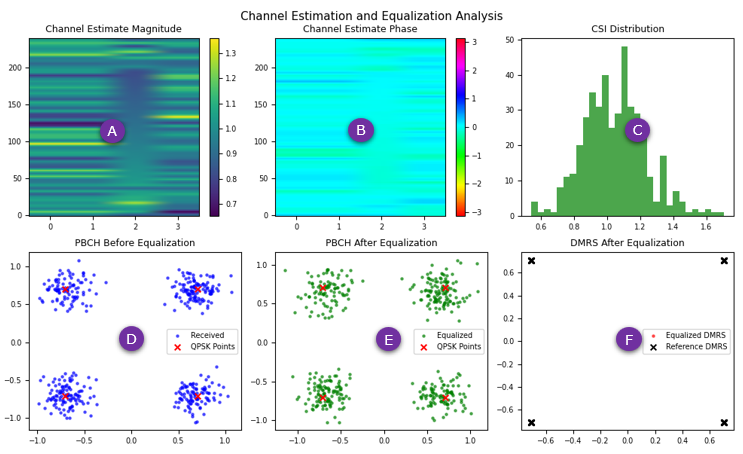
Next step is to perform a detailed visualization of the channel estimation and equalization process applied to the received 5G NR PBCH signal. The top row illustrates key characteristics of the estimated channel: the magnitude and phase distributions across the resource grid, along with a histogram of Channel State Information (CSI) values that reflect signal quality. In the bottom row, constellation diagrams compare PBCH symbols before and after equalization, showing the improvement in symbol
clarity and alignment with ideal QPSK positions. The final plot highlights the equalized DMRS symbols against their reference counterparts, serving as a validation of channel correction accuracy. Altogether, this figure offers insight into how well the receiver characterizes and compensates for the wireless channel's impairments to recover transmitted data.
Preprocess and Calculation
|
import matplotlib.patches as mpatches
if not SKIP_EQUALIZATION:
# Create reference grid with matching dimensions
These lines prepare a template grid (refGrid) that mirrors the structure of the received SSB signal grid (rxGrid). This template grid will then be populated with the known reference signals (specifically the PBCH DMRS) at their correct locations. This refGrid, containing only the known DMRS pilots, is essential for performing channel estimation in the subsequent steps
refGrid = np.zeros((nrbSSB*12, 4), 'complex')
dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab')
Followings are the breakdown and description
- refGrid = np.zeros((nrbSSB*12, 4), 'complex'):
- This creates a new NumPy array named refGrid.
- (nrbSSB*12, 4) specifies the shape of the grid:
- nrbSSB*12: Calculates the number of rows (subcarriers), corresponding to the SSB bandwidth (20 RBs * 12 subcarriers/RB = 240).
- 4: Sets the number of columns to 4, matching the number of OFDM symbols in the processed rxGrid.
- 'complex' sets the data type of the array elements to complex numbers.
- np.zeros(...) initializes all elements in this 240x4 grid to zero (0+0j). This creates an empty grid ready to be filled with known reference symbols.
- dmrsIndices = nrPBCHDMRSIndices(detected_NID, style='matlab'):
- This function call retrieves the resource element indices where the PBCH DMRS symbols are located within the SSB grid structure.
- The DMRS locations depend on the detected_NID.
- These dmrsIndices (likely linear indices) specify where in the refGrid the known DMRS sequence needs to be placed. The style='matlab' argument pertains to the indexing format.
# Set DMRS reference signals
This line takes the known, ideal PBCH DMRS (Demodulation Reference Signal) sequence and places it into the correct time-frequency locations within the refGrid (which was previously initialized as an empty grid of zeros). This step creates a clean reference grid containing only the expected DMRS pilot symbols, which is crucial for comparing against the received grid (rxGrid) to estimate the radio channel conditions.
nrSetResources(dmrsIndices, refGrid, nrPBCHDMRS(detected_NID, ibar_SSB))
Followings are the breakdown and description
- nrSetResources(dmrsIndices, refGrid, nrPBCHDMRS(detected_NID, ibar_SSB)): This function call performs the placement operation:
- nrPBCHDMRS(detected_NID, ibar_SSB): This part first generates the actual complex values of the ideal PBCH DMRS sequence. The sequence depends on the cell ID (detected_NID) and the SSB time index (ibar_SSB) which influences its scrambling.
- dmrsIndices: Provides the specific indices (resource element locations, determined earlier) where the generated DMRS symbols should be placed within the grid.
- refGrid: Specifies the target grid (the 240x4 grid of zeros) where the DMRS symbols will be inserted.
- nrSetResources(...): This function takes the generated DMRS symbols and inserts them into the refGrid at the locations specified by dmrsIndices. Locations not specified in dmrsIndices remain zero
# Channel estimation using reference implementation method
This code performs channel estimation, which is the process of figuring out how the radio channel altered the signal. It does this by comparing the received pilot symbols (DMRS) within rxGrid to the known, ideal DMRS symbols stored in refGrid. By analyzing the differences in amplitude and phase at these known points, the function estimates the channel's effect (represented by H) across the entire time-frequency grid and also estimates the level of noise (nVar) present in the received signal.
with np.errstate(divide='ignore', invalid='ignore'):
H, nVar = nrChannelEstimate(rxGrid=rxGrid, refGrid=refGrid)
Followings are the breakdown and description
- with np.errstate(divide='ignore', invalid='ignore'):: This is a Python context manager used to temporarily change how NumPy handles certain errors or warnings within the indented block.
- divide='ignore': It tells NumPy to ignore warnings that would normally occur if division by zero happens during calculations.
- invalid='ignore': It tells NumPy to ignore warnings related to invalid mathematical operations (like 0/0 which results in NaN - Not a Number).
- Reason: Channel estimation often involves dividing the received signal by the reference signal (rxGrid / refGrid). Since refGrid contains zeros everywhere except at DMRS locations, divisions by zero would occur. This context manager prevents NumPy from flooding the output with warnings, assuming the nrChannelEstimate function is designed to handle these zero divisions appropriately (e.g., by only performing the division where the reference is non-zero).
- H, nVar = nrChannelEstimate(rxGrid=rxGrid, refGrid=refGrid): This is the function call that performs the actual channel estimation.
- rxGrid=rxGrid: Provides the grid of received complex symbols (240x4).
- refGrid=refGrid: Provides the grid containing only the ideal DMRS symbols at their correct locations (and zeros elsewhere).
- nrChannelEstimate: This function takes the received and reference grids and calculates:
- H: An estimate of the channel frequency response. This is typically a complex array of the same shape as rxGrid (240x4). Each element H[f, t] represents the estimated multiplicative distortion (gain and phase shift) introduced by the channel on subcarrier f during OFDM symbol t. The function calculates the channel directly at the DMRS locations (e.g., H_dmrs = rxGrid[dmrs] / refGrid[dmrs]) and then interpolates/extrapolates this information across the rest of the grid.
- nVar: An estimate of the noise variance present in the received signal. This is often calculated by looking at the difference between the received signal and the expected signal (reference signal modified by the estimated channel H) at the pilot locations.
# DMRS equalization
This line performs a basic form of channel equalization specifically on the PBCH DMRS (Demodulation Reference Signal) symbols. It attempts to remove the distorting effects of the radio channel from the received DMRS symbols by dividing the received signal (rxGrid) by the estimated channel response (H). The resulting "channel-corrected" DMRS symbols are then extracted and stored.
PBCHDMRS_wiped = nrExtractResources(dmrsIndices, rxGrid/H)
Followings are the breakdown and description
- rxGrid / H: This performs element-wise division of the received signal grid (rxGrid) by the channel estimate grid (H) calculated in the previous step.
- Conceptually, if the received signal Y at a specific resource element is modeled as Y = H * X + Noise (where X is the transmitted symbol), then dividing Y by H gives Y / H = X + Noise / H.
- This division aims to reverse the channel's multiplicative effect (H), thereby recovering an estimate of the originally transmitted symbol (X), albeit with potentially amplified noise (Noise / H). This technique is known as zero-forcing equalization.
- nrExtractResources(dmrsIndices, rxGrid / H): This function then takes the result of the element-wise division (rxGrid / H) and extracts the values only at the specific locations (dmrsIndices) corresponding to the PBCH DMRS symbols.
- PBCHDMRS_wiped = ...: The extracted, equalized DMRS symbols are stored in the variable PBCHDMRS_wiped. These symbols should ideally resemble the original, known DMRS sequence, allowing for verification of the channel estimation and equalization process (e.g., by plotting their constellation).
# PBCH equalization using MMSE
This block performs channel equalization specifically on the symbols intended for the Physical Broadcast Channel (PBCH) data, using the Minimum Mean Square Error (MMSE) technique. Unlike simple zero-forcing, MMSE equalization considers both the estimated channel effect (H) and the estimated noise level (nVar) to calculate an equalization filter that optimally reverses the channel distortion while minimizing noise amplification. The outputs are the equalized PBCH symbols (pbch_eqed) ready for demodulation, and Channel State Information (csi) values indicating the quality/reliability of the channel at those locations.
pbchIndices = nrPBCHIndices(detected_NID)
pbch_eqed, csi = nrEqualizeMMSE(nrExtractResources(pbchIndices, rxGrid), nrExtractResources(pbchIndices, H), nVar)
Followings are the breakdown and description
- pbchIndices = nrPBCHIndices(detected_NID): Retrieves the standard resource element indices corresponding to all locations allocated to the PBCH (including potential DMRS locations at this stage) based on the detected_NID. This is needed to extract the relevant received symbols and their corresponding channel estimates.
- pbch_eqed, csi = nrEqualizeMMSE(...): This is the function call that performs MMSE equalization and returns the results.
- nrExtractResources(pbchIndices, rxGrid): Extracts the complex values from the received grid (rxGrid) at all the potential PBCH locations specified by pbchIndices. This provides the input signal (Y) to the equalizer.
- nrExtractResources(pbchIndices, H): Extracts the complex channel estimates from the channel estimation grid (H) at the same potential PBCH locations. This provides the channel estimate (H_est) relevant to the PBCH symbols.
- nVar: Passes the previously estimated noise variance to the function. MMSE uses nVar to balance channel inversion against noise enhancement.
- nrEqualizeMMSE(...): This function implements the MMSE algorithm. For each PBCH resource element, it calculates an equalization coefficient (conceptually conj(H_est) / (|H_est|^2 + nVar)) and multiplies the corresponding received symbol (Y) by it. This process aims to produce the best estimate of the originally transmitted symbol in the presence of noise. It likely internally handles or ignores the DMRS locations included in pbchIndices to focus on the data symbols.
- Outputs:
- pbch_eqed: A 1D array containing the complex values of the PBCH data symbols after equalization. These should ideally be close to the original QPSK constellation points.
- csi: A 1D array containing Channel State Information values for each corresponding equalized PBCH symbol. CSI reflects the estimated quality or reliability of the channel (e.g., Signal-to-Noise Ratio) at that specific resource element. Higher CSI indicates a more reliable symbol, which is valuable for soft-decision decoding later.
# Calculate EVM
This line calculates the Error Vector Magnitude (EVM) for the equalized PBCH data symbols (pbch_eqed). EVM is a standard metric used to quantify the quality of a digitally modulated signal by measuring the difference between the actual received constellation points (after equalization) and their ideal target locations. A lower EVM value indicates a cleaner signal with less distortion and noise.
evm = np.sum(np.abs(pbch_eqed - nrSymbolModulate(nrSymbolDemodulate(pbch_eqed, 'QPSK', 1, 'hard'), 'QPSK'))) / pbch_eqed.shape[0]
Followings are the breakdown and description
- nrSymbolDemodulate(pbch_eqed, 'QPSK', 1, 'hard'):
- This performs hard-decision demodulation on the equalized PBCH symbols (pbch_eqed).
- For each complex symbol in pbch_eqed, it determines which of the 4 ideal QPSK constellation points it is closest to.
- It outputs the result of this decision, likely as integer indices or bit pairs representing the decided symbol.
- nrSymbolModulate(..., 'QPSK'):
- This takes the hard decisions from the previous step.
- It maps these decisions back to the corresponding ideal complex QPSK constellation point values (e.g., points like (+/-1 +/- 1j)/sqrt(2) assuming standard normalization).
- The output is an array containing the ideal reference constellation point for each of the received symbols.
- pbch_eqed - nrSymbolModulate(...):
- This calculates the error vector for each symbol by subtracting the ideal reference point (determined above) from the actual received, equalized symbol (pbch_eqed). The result is an array of complex numbers, each representing the error vector (magnitude and phase difference).
- np.abs(...):
- Calculates the absolute value (magnitude or length) of each complex error vector.
- np.sum(...):
- Sums the magnitudes of all the individual error vectors.
- / pbch_eqed.shape[0]:
- Divides the total sum of error magnitudes by the number of PBCH symbols (pbch_eqed.shape[0] gives the size of the array).
- evm = ...:
- The final result, representing the average magnitude of the error vector across all PBCH symbols, is assigned to the variable evm. (Note: EVM is often expressed as a percentage or in dB relative to a reference power/amplitude, but this calculation gives the average absolute error magnitude).
|
Channel Estimate Magnitude - (A)
This plot visualizes the magnitude of the estimated channel matrix, providing insight into how much gain or attenuation each resource element experienced as the signal propagated through the wireless channel. The channel matrix H is computed using the nrChannelEstimate function, which compares the received grid against known reference signals. Taking the absolute value of H reveals the signal strength variations across the time-frequency grid, and the result is rendered using a color map to
highlight areas of strong and weak reception. This helps assess the reliability of different regions in the SSB grid.
|
ax_ch_mag = fig_eq.add_subplot(eq_grid[0, 0])
ch_mag_plot = ax_ch_mag.imshow(np.abs(H), origin='lower', aspect='auto', cmap='viridis')
|
- H is the estimated channel matrix computed using:
- H, nVar = nrChannelEstimate(rxGrid=rxGrid, refGrid=refGrid)
- np.abs(H) gives the magnitude of each complex channel estimate.
- This plot shows how much gain each resource element experienced through the channel.
Channel Estimate Phase - (B)
This plot displays the phase component of the estimated channel matrix, offering a view into how the signal’s phase has been altered during transmission. The phase is extracted from the complex channel estimate H using np.angle(H), and is visualized using an HSV colormap to represent the full range from −π to π. Variations in phase across the grid can reveal frequency offsets, Doppler shifts, or multipath effects that cause distortion in the received signal. This visualization is critical for
understanding the non-amplitude-related impairments introduced by the wireless channel.
|
ax_ch_phase = fig_eq.add_subplot(eq_grid[0, 1])
ch_phase_plot = ax_ch_phase.imshow(np.angle(H), origin='lower', aspect='auto', cmap='hsv',
vmin=-np.pi, vmax=np.pi)
|
- np.angle(H) extracts the phase of each channel estimate.
- The HSV colormap helps visualize the phase spectrum between −π and π
- Phase distortion can indicate the presence of frequency offset or multipath effects.
CSI Distribution (Channel State Information) - (C)
This histogram visualizes the distribution of Channel State Information (CSI) values obtained during the MMSE equalization process. CSI reflects the reliability or confidence of each equalized PBCH symbol and is computed alongside the equalized signal using the nrEqualizeMMSE function. By plotting the frequency of CSI values across all PBCH resource elements, this chart provides a statistical view of how well the channel was estimated and how trustworthy each demodulated bit is likely to be
under current conditions.
|
ax_csi = fig_eq.add_subplot(eq_grid[0, 2])
ax_csi.hist(csi, bins=30, color='green', alpha=0.7)
|
- csi is computed during MMSE equalization:
- pbch_eqed, csi = nrEqualizeMMSE(...)
- The histogram shows the distribution of CSI values across PBCH REs, indicating the reliability or confidence in each equalized symbol.
PBCH Constellation Before Equalization - (D)
This constellation plot presents the received PBCH symbols before any channel equalization is applied, offering a raw view of how the signal has been distorted during transmission. The variable pbchRx holds the PBCH samples extracted from the resource grid, excluding any DMRS positions. These samples are plotted in blue. For comparison, the four ideal QPSK constellation points are shown in red, serving as a reference to highlight how far the received symbols have deviated due to channel effects
such as fading, noise, and interference.
|
ax_before = fig_eq.add_subplot(eq_grid[1, 0])
ax_before.scatter(pbchRx.real, pbchRx.imag, c='blue', alpha=0.6, s=20, marker='.', label='Received')
ax_before.scatter(qpsk_points.real, qpsk_points.imag, c='red', s=30, marker='x', label='QPSK Points')
|
- pbchRx contains raw PBCH samples (excluding DMRS) extracted directly from rxGrid.
- qpsk_points defines the four ideal constellation points for QPSK.
- This plot shows how distorted the PBCH symbols are before applying channel equalization.
PBCH Constellation After Equalization - (E)
This plot displays the constellation of PBCH symbols after applying MMSE equalization, revealing the effectiveness of channel compensation. The variable pbch_eqed contains the equalized PBCH samples, computed using the nrEqualizeMMSE function. These are plotted in green, showing their post-equalization positions. The ideal QPSK constellation points remain overlaid in red for comparison. The improved clustering of received symbols around the ideal points indicates that the equalization has successfully
mitigated channel effects, resulting in cleaner and more reliable demodulation.
|
ax_after = fig_eq.add_subplot(eq_grid[1, 1])
ax_after.scatter(pbch_eqed.real, pbch_eqed.imag, c='green', alpha=0.6, s=20, marker='.', label='Equalized')
ax_after.scatter(qpsk_points.real, qpsk_points.imag, c='red', s=30, marker='x', label='QPSK Points')
|
- pbch_eqed is the MMSE-equalized PBCH signal obtained from:
- pbch_eqed, csi = nrEqualizeMMSE(...)
- This shows that after equalization, received points better align with ideal QPSK symbols, indicating improved demodulation conditions.
NOTE :Why the PBCH Equalization Result is not good ?
If you had keen eyes on the result, you might notice that there are not so much difference between PBCH before equalization and after equalization. More strictly it may look as if the constellation got even worse after equalization, whereas the result of equalization for PBCH DMRS is perfect. At first, I thought there might be some issues with channel estimation and equalization process itself. and spent a lot of time trying to improve this by trying all different idea that I can think of but
nothing worked. Finally I got to understand there is reason for this kind of result and it is not because of the channel estimation and equalization method but because of the characteristics of noise applied to the signal.
The poor equalization performance despite good DMRS equalization can be explained by the nature of AWGN (Additive White Gaussian Noise) in our simulation. Let me explain why:
- AWGN Properties:
- AWGN is statistically independent across time and frequency
- It has zero mean and constant variance
- Most importantly, it has no correlation between different time/frequency positions
- Our Current Setup:
- We're adding AWGN with TARGET_SNR_DB = 5 to the waveform
- The channel estimation is based on DMRS positions
- There's no actual channel distortion (no fading, no frequency selectivity, no time variation)
- Why DMRS Equalization Looks Good:
- The DMRS positions show good equalization because we know the exact reference symbols
- When we divide received DMRS by channel estimate at DMRS positions, we're essentially removing the AWGN at those specific points
- The DMRS constellation looks good because we're comparing against known reference points
- Why PBCH Equalization Doesn't Help:
- The channel estimate from DMRS positions can't help with AWGN at PBCH positions because:
- AWGN at PBCH positions is completely independent of AWGN at DMRS positions
- There's no actual channel to estimate (just noise)
- When we apply the channel estimates to PBCH positions, we're essentially:
- Not correcting any real channel effects (because there aren't any)
- Potentially introducing additional distortion by applying corrections based on uncorrelated noise
This explains why:
- DMRS equalization looks good (we're comparing against known references)
- PBCH equalization doesn't improve the signal (can't correct independent AWGN)
- We still get successful decoding (the AWGN level is manageable for the error correction)
To make the equalization more meaningful, we would need to:
- Add actual channel effects (like frequency selective fading)
- Add correlated noise or interference
- Introduce timing or frequency offsets
These would create distortions that are correlated across the resource grid, making channel estimation and equalization more effective and necessary.
The degradation of the PBCH constellation after equalization can be directly explained by the AWGN nature. Let me break down why the equalization actually makes things worse in this case:
- What's Happening in Our System:
Received Signal = Original Signal + AWGN
At DMRS positions: R_dmrs = D + N1
At PBCH positions: R_pbch = P + N2
where N1 and N2 are independent AWGN samples
- Channel Estimation Process:
- At DMRS positions, we estimate H = R_dmrs/D = (D + N1)/D ≈ 1 + N1/D
- This channel estimate contains noise but no real channel distortion
- Why Equalization Makes PBCH Worse:
We apply this noisy channel estimate to PBCH: R_pbch/H
This becomes: (P + N2)/(1 + N1/D)
(P + N2)/(1 + N1/D) ≈ (P + N2)(1 - N1/D)
= P - PN1/D + N2 - N2N1/D
- We end up with:
- Original PBCH signal (P)
- Original AWGN at PBCH position (N2)
- Additional noise term from DMRS (-PN1/D)
- Cross-noise term (-N2N1/D)
- The Result:
- Instead of just having one noise term (N2)
- We now have three noise terms (N2, -PN1/D, -N2N1/D)
- This explains why the constellation looks more scattered after equalization
This is a classic case where trying to correct a non-existent channel distortion actually introduces more distortion. The equalization process is essentially:
- Creating a noisy channel estimate from DMRS positions
- Applying this noisy estimate to PBCH positions where the noise is completely uncorrelated
- Multiplying uncorrelated noise terms together, which increases the overall noise power
This is why in systems with only AWGN and no actual channel distortion, it's often better to skip equalization entirely. The equalization process is designed to correct correlated channel effects, not uncorrelated noise.
DMRS Constellation After Equalization - (F)
This plot shows the constellation of DMRS symbols after channel equalization, providing a direct validation of the channel estimation's accuracy. The equalized DMRS samples, stored in dmrs_eq, are computed by dividing the received values in rxGrid by the corresponding estimated channel values in H. These samples are plotted in red. The known reference symbols, dmrsRef, are overlaid in black to serve as a ground truth. A tight alignment between the equalized and reference symbols indicates that
the channel estimation was accurate, ensuring effective equalization and reliable decoding of the PBCH.
|
ax_dmrs = fig_eq.add_subplot(eq_grid[1, 2])
dmrs_eq = rxGrid[freq_indices, symbol_indices] / H[freq_indices, symbol_indices]
ax_dmrs.scatter(dmrs_eq.real, dmrs_eq.imag, c='red', alpha=0.6, s=20, marker='.', label='Equalized DMRS')
ax_dmrs.scatter(dmrsRef.real, dmrsRef.imag, c='black', s=30, marker='x', label='Reference DMRS')
|
- dmrs_eq is calculated by directly dividing the received DMRS samples by their estimated channel values:
- dmrs_eq = rxGrid[dmrs_indices] / H[dmrs_indices]
- dmrsRef is the known reference sequence.
- This validates how well the channel estimation worked by comparing equalized DMRS symbols to their ideal values.
The PBCH decoding process in the code is the final stage of the 5G NR synchronization and demodulation pipeline. After detecting, demodulating, and equalizing the PBCH symbols, this stage attempts to recover the system information bits broadcast in the PBCH payload using channel decoding techniques specified by 3GPP.
Preprocess and Calculation
This code block attempts to demodulate and decode the Physical Broadcast Channel (PBCH) payload, containing crucial system information. It first selects either the channel-equalized or raw PBCH symbols based on a flag. It then performs an initial attempt at soft demodulation (converting QPSK symbols to Log-Likelihood Ratios), descrambles the resulting bits using a sequence derived from the detected cell ID and SSB time index (ibar_SSB), applies channel state information (CSI) for reliability weighting, performs rate recovery specific to polar codes, and finally decodes the polar code. However, recognizing that the initial SSB index detection (ibar_SSB) might be ambiguous or incorrect for scrambling, the code implements a robust recovery mechanism. It systematically retries the entire process within nested loops, iterating through both hard and soft demodulation methods and testing all possible SSB indices (v from 0 to 7) for the descrambling step, until the decoded payload successfully passes a CRC check, indicating correct recovery of the PBCH information.
|
# Use either equalized or raw PBCH symbols based on flag
pbch_for_demod = pbch_eqed if not SKIP_EQUALIZATION else pbchRx
# PBCH demodulation and rate recovery
pbchBits = nrSymbolDemodulate(pbch_for_demod, 'QPSK', nVar, 'soft')
E = 864
v = ibar_SSB
scrambling_seq = nrPBCHPRBS(detected_NID, v, E)
scrambling_seq_bpsk = (-1)*scrambling_seq*2 + 1
pbchBits_descrambled = pbchBits * scrambling_seq_bpsk
pbchBits_csi = pbchBits_descrambled * np.repeat(csi, 2)
# Polar code parameters
A = 32 # Information bits
P = 24 # CRC bits
K = A + P # Total bits including CRC
N = 512 # Mother code size, from 3GPP TS 38.212 Section 5.3.1
# Rate recovery and polar decoding
decIn = nrRateRecoverPolar(pbchBits_csi, K, N, False, discardRepetition=False)
decoded = nrPolarDecode(decIn, K, 0, 0)
# First instance - initial decoding
# CRC check
decoded3, crc_result = nrCRCDecode(decoded, '24C')
# Try both hard and soft demodulation
demod_methods = ['hard', 'soft']
for demod_method in demod_methods:
print(f"\n--- Using {demod_method} demodulation ---")
# Try different SSB indices
for v in range(8): # Try v = 0-7
print(f"\nTrying SSB index v = {v}")
# Adjust noise variance based on demodulation method
if demod_method == 'soft':
# Use the global nVar for soft demodulation - already defined at the top
# Get PBCH bits through soft demodulation
pbchBits = nrSymbolDemodulate(pbch_for_demod, 'QPSK', nVar, 'soft')
else:
# For hard demodulation, get binary decisions first
pbchBits_hard = nrSymbolDemodulate(pbch_for_demod, 'QPSK', 1, 'hard')
# Convert to ±1 format for descrambling
pbchBits = pbchBits_hard * 2 - 1 # Convert 0/1 to -1/+1
# PBCH descrambling
E = 864 # Number of channel bits
scrambling_seq = nrPBCHPRBS(detected_NID, v, E)
scrambling_seq_bpsk = (-1)*scrambling_seq*2 + 1 # Convert 0/1 to -1/+1
pbchBits_descrambled = pbchBits * scrambling_seq_bpsk
# For soft demodulation, apply CSI (if available from equalization)
if demod_method == 'soft':
if not SKIP_EQUALIZATION:
# If equalization was performed, use the CSI values
pbchBits_csi = pbchBits_descrambled * np.repeat(csi, 2)
else:
# Use moderate confidence since we're using fixed noise variance
csi_fixed = np.ones(E//2) * 5
pbchBits_csi = pbchBits_descrambled * np.repeat(csi_fixed, 2)
else:
# For hard demodulation, we already have ±1 values
pbchBits_csi = pbchBits_descrambled
# Convert back to binary for nrRateRecoverPolar if using hard demodulation
if demod_method == 'hard':
pbchBits_csi = (pbchBits_csi + 1) / 2 # Convert -1/+1 to 0/1
# Polar decoding parameters
A = 32 # Information bits
P = 24 # CRC bits
K = A + P # Total bits including CRC
N = 512 # Mother code size, from 3GPP TS 38.212 Section 5.3.1
# Rate recovery and polar decoding
decIn = nrRateRecoverPolar(pbchBits_csi, K, N, False, discardRepetition=False)
decoded = nrPolarDecode(decIn, K, 0, 0)
# Second instance - in the demodulation methods loop
# CRC check
decoded3, crc_result = nrCRCDecode(decoded, '24C')
if crc_result == 0:
print(f"nrPolarDecode: PBCH CRC ok for v = {v} with {demod_method} demodulation")
print(f"Decoded bits: {[int(bit[0]) for bit in decoded3]}")
# If successful, no need to try other values
break
else:
print(f"nrPolarDecode: PBCH CRC failed for v = {v} with {demod_method} demodulation")
|
Symbol Demodulation
This part of the PBCH decoding process performs symbol demodulation, where the received PBCH QPSK symbols are converted into soft bits. The input pbch_for_demod includes either the raw or equalized PBCH symbols, depending on whether channel equalization was applied earlier. The function nrSymbolDemodulate processes these symbols using the QPSK scheme and outputs log-likelihood values (soft bits), which represent the confidence of each bit being a 0 or 1. The demodulation behavior is influenced
by the noise variance parameter nVar, ensuring that the resulting soft bits are scaled appropriately based on signal conditions.
|
pbchBits = nrSymbolDemodulate(pbch_for_demod, 'QPSK', nVar, 'soft')
|
- pbch_for_demod contains the PBCH symbols—either raw or equalized, depending on whether equalization was skipped.
- The function nrSymbolDemodulate converts QPSK symbols into soft bits (log-likelihood values), which provide confidence levels for each bit.
- The demodulation uses nVar (noise variance) to shape the soft decision process.
PBCH Descrambling
This step performs PBCH descrambling by removing the cell-specific scrambling applied during transmission. The scrambling sequence is generated using the function nrPBCHPRBS, based on the detected physical cell ID (detected_NID), the SSB index v, and the length E of the PBCH bitstream. The binary sequence is then mapped to BPSK format (values of +1 or –1) to create scrambling_seq_bpsk. By multiplying the demodulated soft bits with this sequence, the receiver effectively reverses the scrambling,
recovering the original encoded PBCH data prior to channel coding.
|
scrambling_seq = nrPBCHPRBS(detected_NID, v, E)
scrambling_seq_bpsk = (-1) * scrambling_seq * 2 + 1
pbchBits_descrambled = pbchBits * scrambling_seq_bpsk
|
- The PBCH uses a cell-specific scrambling sequence, generated from the detected physical cell ID detected_NID and the SSB index v.
- The binary scrambling sequence is mapped to BPSK format (+1 or –1), and then multiplied element-wise with the demodulated bits to descramble them.
CSI Weighting (Optional but important)
This step applies Channel State Information (CSI) weighting to the descrambled PBCH bits, enhancing decoding reliability. CSI reflects the receiver's confidence in each symbol after equalization, and by multiplying the soft bits with the CSI values, the decoder gives more influence to reliable symbols and less to noisy ones. Since QPSK carries two bits per symbol, the CSI vector is duplicated using np.repeat(csi, 2) to match the bit length. Though optional, this weighting is particularly important
in challenging channel conditions to improve polar decoding performance.
|
pbchBits_csi = pbchBits_descrambled * np.repeat(csi, 2)
|
- If equalization was performed, Channel State Information (CSI) is used to weight the bits based on the confidence in each received symbol.
- CSI is repeated twice to match the QPSK's 2 bits per symbol.
Rate Recovery
This step performs rate recovery, which restructures the descrambled and CSI-weighted bitstream into the format required by the polar decoder. Using the nrRateRecoverPolar function, it applies the necessary transformations defined in 3GPP TS 38.212 Section 5.4, including handling of padding, bit repetition, and interleaving. The inputs K and N represent the number of information plus CRC bits and the mother code size, respectively. This transformation ensures that the polar decoder receives
a correctly formatted input for successful decoding of the PBCH payload.
|
decIn = nrRateRecoverPolar(pbchBits_csi, K, N, False, discardRepetition=False)
|
- Converts the descrambled, CSI-weighted bitstream into a format expected by the polar decoder.
- Handles padding, repetition, and reordering as specified in TS 38.212 Section 5.4.
Polar Decoding
This step applies polar decoding to recover the original PBCH message from the rate-recovered bitstream. The function nrPolarDecode implements the standard polar decoding algorithm and takes as input the formatted soft bits decIn, along with the total number of bits K, which includes both the payload and the CRC. Specifically, K = A + P, where A = 32 represents the PBCH payload bits and P = 24 is the CRC length. The decoder processes the input using frozen bits and decoding steps defined in
the 5G NR specifications to output the most likely transmitted bit sequence.
|
decoded = nrPolarDecode(decIn, K, 0, 0)
|
- Uses the polar decoding algorithm to recover the original message.
- K = A + P where:
- A = 32 bits of actual PBCH payload,
- P = 24 bits of CRC.
CRC Check
This final step validates the decoded PBCH message by performing a CRC check. The nrCRCDecode function takes the output of the polar decoder and applies the 24-bit CRC algorithm ('24C') to determine whether the message was decoded correctly. It returns both the final decoded bits (decoded3) and a crc_result flag. If crc_result equals 0, it indicates that the CRC matched, confirming successful decoding of the PBCH payload. Otherwise, the decoding is considered to have failed due to bit errors.
|
decoded3, crc_result = nrCRCDecode(decoded, '24C')
|
- Checks whether the decoded message has a valid CRC.
- If crc_result == 0, the decoding is considered successful.
SSB Index Search Loop
Since the correct SSB index v is not known in advance, the code performs a brute-force search by looping through all eight possible SSB indices. For each value of v, it regenerates the descrambling sequence, demodulates and decodes the PBCH, and checks the CRC. The loop stops as soon as a valid CRC is detected, indicating that the correct SSB index and corresponding system information have been successfully recovered. This approach ensures robustness when multiple SSBs are transmitted with
different configurations.
|
for v in range(8):
...
if crc_result == 0:
print(f"nrPolarDecode: PBCH CRC ok for v = {v}")
break
|
- This brute-force loop tries all possible SSB indices to find the correct one by checking which descrambling key leads to a valid CRC.
Reference
|
|


