5G/NR - Pre Trial - Pseudo Random Sequence  

  

 

 

 

NOTE : This note is about a tempary 5G specification that was implemented and tried before 5G specification is finalized. I keep this note for study purpose.

 

Pseudo Random Sequence 

 

The two most famous numerical sequence in both LTE and 5G Pretrial is Zadoff Chu sequence and Pseudo Random sequence. Sequence Generation algorithm for these two sequence is almost same in both LTE and 5G Pretrial, but these sequence are more widely used in 5G Pretrial specification. Followings are the list of applications of these sequences.

 

Sequence Type

Application

Zadoff Chu Sequence

6.8.1 Primary Synchronization Signal
6.8.3 Extended Synchronization Signal

5.5.4 Sounding reference signal

5.7.2 Preamble sequence generation (PRACH)
 

Psuedo Random Sequence :

Gold Code (Gold Sequence)

6.5.1 Scrambling (xPDSCH)

6.5A.1 Scrambling (ePBCH)

5.5.2 Demodulation reference signal associated with xPUCCH

5.5.3 Demodulation reference signal associated with xPUSCH

5.5.5 Phase noise compensation reference signal

6.6.2 xPDCCH multiplexing and scrambling

6.7.1 UE-specific reference signals associated with xPDSCH

6.7.2 UE-specific reference signals associated with xPDCCH

6.7.3 CSI reference signals

6.7.4 Beam reference signal (BRS)

6.7.5 Beam refinement reference signals

6.7.6 DL Phase noise compensation reference signal

6.7.7 Demodulation reference signals associated with ePBCH

6.8.2 Secondary Synchronization Signal
6.8.3 Extended Synchronization Signal (Scrambling a ZadOff-Chu Seq)

 

 

As in LTE, the Pseudo Random Sequence in 5G trial is a kind of Gold Sequence and it is based on a common form as shown below. This algorithm is exactly same as LTE pseudo random sequence. (So I recommed you to read through LTE Pseduo Random Sequence page as well since I put more descriptions in the page).

 

 

How do we utilize this single mathematical form to such a many different application ? First trick is to use different 'n' in c(n). The second, more important, is to use different initialization value. The initialization value gets different depending on applications.  I put down all the initialization value for each and every application listed in the table shown above.  You don't have to memorize nor try to understand these equation itself, just try to figure out what kind of parameters are involved in determining the initialization value for each application. Some of these parameters are from RRC message or DCI, these values shown here will help you understand those RRC / DCI parameters.

 

 

 

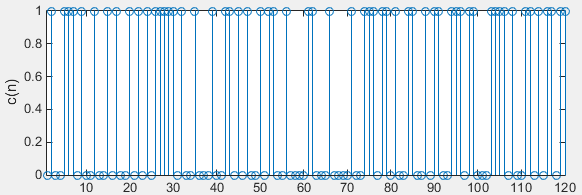
Following is an example of the sequence when n = 119 (120 data point) and the initialization value is 64.

 

x2_init

Sequence Plot

x2_init = 64

 

 

Disclaimer : This code is just to push myself (probably readers) to look into the algorithm (formula) specified in the specification to the most detailed level. If you try to convert the specification into the programming code whatever language you choose, you will understand the equation / algorithm in much more detailed level than just reading the document. However, this code has not been verified with any real data.

 

Filename : Generate_PR.m

Last Update : Dec 18, 2016

%V5G.211 - 7.2

function PRB = Generate_PR(PR)

 

    % Initial condition of the polynomia x1(). This is fixed value as described in 36.211 7.2

    x1_init = [1 0 0 0 0 0 0 0 0 0 ...

               0 0 0 0 0 0 0 0 0 0 ...

               0 0 0 0 0 0 0 0 0 0 ...

               0];

 

    % Initial condition of the polynomia x2().

    % This is supposed to be used as c_init as described in 36.211 7.2

    % But for simplicity, I just se the arbitrary value for now

    x2_init = de2bi(PR.x2_init,31,'left-msb');

    

    % Mpn is the length of the final sequence c()

    % '1' is added because of Matlab Array Index starts with '1'

    Mpn = PR.n + 1;

 

    % Nc as defined in 36.211 7.2

    Nc = 1600;

 

    % Create a vector(array) for x1() and x2() all initialized with 0

    x1 = zeros(1,Nc + Mpn + 31);

    x2 = zeros(1,Nc + Mpn + 31);

 

    % Create a vector(array) for c() all initialized with 0

    c = zeros(1,Mpn);

 

    % Initialize x1() and x2()

    x1(1:31) = x1_init;

    x2(1:31) = x2_init;

 

    % generate the m-sequence : x1()

    for n = 1 : (Mpn+Nc)    

       x1(n+31) = mod(x1(n+3) + x1(n),2);

    end;

 

    % generate the m-sequence : x2()

    for n = 1 : (Mpn+Nc)    

       x2(n+31) = mod(x2(n+3) + x2(n+2) + x2(n+1) + x2(n),2);

    end;

    

    n = Mpn;

    c(n)= mod(x1(n+Nc) + x2(n+Nc),2);

    PRB = c(n);

    

end

 

 

Filename : Test_Generation_PR.m

Last Update : Dec 18, 2016

prbs = [];

 

PR.x2_init = 64;

 

for n = 0 : 119

  PR.n = n;

  prb = Generate_PR(PR);

  prbs = [prbs prb];

end;

 

stem(prbs);xlim([1 length(prbs)]); ylabel('c(n)');