5G/NR - Pre Trial - Physical Signal - PSS

 

 

 

 

NOTE : This note is about a tempary 5G specification that was implemented and tried before 5G specification is finalized. I keep this note for study purpose.

 

SSS (Secondary Synchronization Signal)

 

SSS is a specific physical layer signal that is used for radio frame synchronization. It has characterstics as listed below.

  • Mapped to 72 active sub carriers, located above the PSS at every OFDM symbols in Subframe 0 and at every OFDM symbols in Subframe 25. (Note : the 5 subcarriers at the bottom and top (10 subcarriers in total) are not allocated any data, meaning only 62 subcarriers carries the real SSS data)

  • Made up of 62 Gold Sequence Values

  • Used for Downlink Frame Synchronization

  • One of the critical factors determining Physical Cell ID

 

 

Baseband Signal Generation

 

The signal generation algorithm of Pretrial SSS is same as LTE SSS. It generate 512 different Gold sequences that are made up of 62 data points as shown below. This is same as LTE SSS signal generation.  512 different Gold Sequence is distictively generated by the two parameter NID(1) and NID(2). NID(1) can be 0 or 1 or 2. NID(2) can be any value from 0 through 167.

 

One example of SSS sequence is shown below.

 

NID

Sequence Plot

NID1 = 0

NID2 = 0

 

Disclaimer : This code is just to push myself (probably readers) to look into the algorithm (formula) specified in the specification to the most detailed level. If you try to convert the specification into the programming code whatever language you choose, you will understand the equation / algorithm in much more detailed level than just reading the document. However, this code has not been verified with any real data.

 

Filename : Generate_Sss.m

Last Update : Dec 16, 2016

%V5G.211 - 6.8.2.1

function SequenceSss = Generate_Sss(SSS)

 

    NID1 = SSS.NID1;

    NID2 = SSS.NID2;

    SUBFRAME = SSS.SubFrame;

    

    q_prime = floor(NID1/30);

    q = floor(((NID1+q_prime*(q_prime+1)/2))/30);

    m_prime = NID1 + q *(q+1)/2;

    m0 = mod(m_prime, 31);

    m1 = mod(m0 + floor(m_prime/31)+1,31);

 

    %%%%%%%%%%%%%%%%% generate d_even() sequence %%%%%%%%%%%%%%%%

    % Generate the sequence x_s() : x() for calculating s_tilda()

    x_s = zeros(1,31);

    x_s(1:5) = [0 0 0 0 1];

 

    for i = 0:25

        x_s((i+5)+1) = mod(x_s(i+2+1)+x_s(i+1),2);

    end;

 

    % Generate the sequence x_c() : x() for calculating c_tilda()

    x_c = zeros(1,31);

    x_c(1:5) = [0 0 0 0 1];

 

    for i = 0:25

        x_c((i+5)+1) = mod(x_c(i+3+1)+x_c(i+1),2);

    end;

 

    % Generate the sequence s_tilda()

    s_tilda = zeros(1,31);

    for i = 0:30

        s_tilda(i+1) = 1 - 2*x_s(i+1);

    end;

 

    % Generate the sequence c_tilda()

    c_tilda = zeros(1,31);

    for i = 0:30

        c_tilda(i+1) = 1 - 2*x_c(i+1);

    end;

 

    % Generate s0_m0_even()

    s0_m0_even = zeros(1,31);

    for n = 0:30

        s0_m0_even(n+1) = s_tilda(mod(n+m0,31)+1);

    end;

    

    % Generate s1_m1_even()

    s1_m1_even = zeros(1,31);

    for n = 0:30

        s1_m1_even(n+1) = s_tilda(mod(n+m1,31)+1);

    end;

 

    % Generate c0_even()

    c0_even = zeros(1,31);

    for n = 0:30

        c0_even(n+1) = c_tilda(mod(n+NID2,31)+1);

    end;

 

     

    % Calculate d_even_sub0

    d_even_sub0 = s0_m0_even .* c0_even;

    

    % Calculate d_even_sub25

    d_even_sub25 = s1_m1_even .* c0_even;

 

    %%%%%%%%%%%%%%%%% generate d_odd() sequence %%%%%%%%%%%%%%%%

    % Generate the sequence x_s() : x() for calculating s_tilda()

    x_z = zeros(1,31);

    x_z(1:5) = [0 0 0 0 1];

 

    for i = 0:25

        x_z((i+5)+1) = mod(x_z(i+4+1) + x_z(i+2+1) + x_z(i+1+1)+ x_z(i+1),2);

    end;

 

    % Generate the sequence z_tilda()

    z_tilda = zeros(1,31);

    for i = 0:30

        z_tilda(i+1) = 1 - 2*x_z(i+1);

    end;

 

    % Generate s1_m1_odd()

    s1_m1_odd = zeros(1,31);

    for n = 0:30

        s1_m1_odd(n+1) = s_tilda(mod(n+m1,31)+1);

    end;

    

    % Generate s0_m0_odd()

    s0_m0_odd = zeros(1,31);

    for n = 0:30

        s0_m0_odd(n+1) = s_tilda(mod(n+m0,31)+1);

    end;

 

    % Generate c1_odd()

    c1_odd = zeros(1,31);

    for n = 0:30

        c1_odd(n+1) = c_tilda(mod(n+NID2+3,31)+1);

    end;

 

    % Generate z1_m0_odd()

    z1_m0_odd = zeros(1,31);

    for n = 0:30

        z1_m0_odd(n+1) = z_tilda(mod(n+mod(m0,8),31)+1);

    end;

    

    % Generate z1_m1_odd()

    z1_m1_odd = zeros(1,31);

    for n = 0:30

        z1_m1_odd(n+1) = z_tilda(mod(n+mod(m1,8),31)+1);

    end;

 

    % Calculate d_odd_sub0

    d_odd_sub0 = s1_m1_odd .* c1_odd .* z1_m0_odd;

    

    % Calculate d_odd_sub25

    d_odd_sub25 = s0_m0_odd .* c1_odd .* z1_m1_odd;

    

    % Calculate d_sub0

    SequenceSss.Subframe0 = zeros(1,62);

    SequenceSss.Subframe0(1:2:end-1) = d_even_sub0;

    SequenceSss.Subframe0(2:2:end) = d_odd_sub0;

    

    % Calculate d_sub25

    SequenceSss.Subframe25 = zeros(1,62);

    SequenceSss.Subframe25(1:2:end-1) = d_even_sub25;

    SequenceSss.Subframe25(2:2:end) = d_odd_sub25;

    

end

 

 

Filename : PlotSequence_Sss.m

Last Update : Dec 16, 2016

function h=PlotSequence_Sss(SssSequence,PlotOption)

    

    xmin = PlotOption.xmin;

    xmax = PlotOption.xmax;

    ymin = PlotOption.ymin;

    ymax = PlotOption.ymax;

    

    subplot(2,5,1);

    plot(real(SssSequence.Subframe0),imag(SssSequence.Subframe0), ...

        'ro','MarkerFaceColor',[1 0 1]);

    axis([xmin xmax ymin ymax]);

    subplot(2,5,[2 5]);

    plot(real(SssSequence.Subframe0),'ro-');xlim([0 length(SssSequence.Subframe0)]);

    title('Subframe 0');

    

    subplot(2,5,6);

    plot(real(SssSequence.Subframe25),imag(SssSequence.Subframe25), ...

        'ro','MarkerFaceColor',[1 0 1]);

    axis([xmin xmax ymin ymax]);

    subplot(2,5,[7 10]);

    plot(real(SssSequence.Subframe25),'ro-');xlim([0 length(SssSequence.Subframe25)]);

    title('Subframe 25');

    

end

 

 

Filename : Test_Generation_Sss.m

Last Update : Dec 16, 2016

 

SSS.NID1 = 0;

SSS.NID2 = 0;

SSS.SubFrame = 25;

 

SssSequence = Generate_Sss(SSS);

 

PlotOption.xmin = -1.5;

PlotOption.xmax = 1.5;

PlotOption.ymin = -1.5;

PlotOption.ymax = 1.5;

 

PlotSequence_Sss(SssSequence,PlotOption);

 

 

 

RE Mapping(Resource Element Mapping) of SSS

 

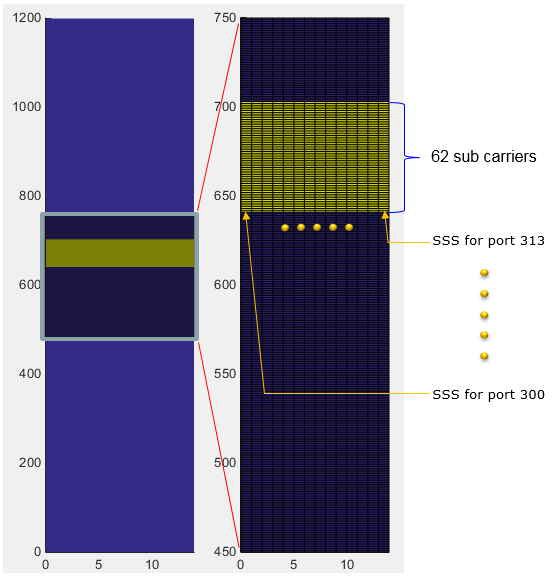
The location of SSS within a radio frame is as highlighed in red box below. It is at the center of the frequency domain in subframe 0 and 25.

 

 

 

If you cut out only subframe 0 and maginify the resource elements above PSS, it looks as shown below. In case of LTE SSS, it occupies only one OFDM symbol but in 5G Pretrial it occupies the whole subframe (i.e, 14 OFDM Symbols). Why it use 14 OFDM symbols ? Actually, the data being carried by each OFDM symbol is same in every symbol. The difference is with antenna ports. As you see below, each of OFDM symbol for PSS is mapped to different antenna ports. These antenna ports will use different Beam Configuration.

In short, the same SSS signal is being transmitted in every symbols in subframe 0 and 25 with different beam direction for each symbol. (If you are interested in the fundamental idea of this type of transmission, refer to Synchronization Signal in a frame structure).

 

Matlab Code :  SSS