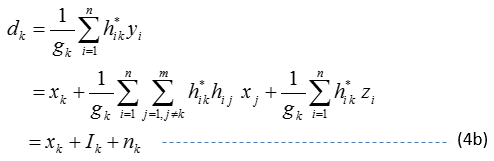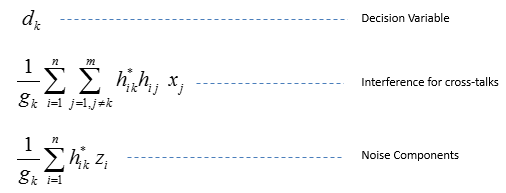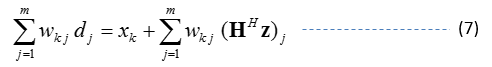|
Communication Technology |
||
|
Zero Forcing Model
This page (knowledge) is shared by James Weng who is a real expert in this area.
Consider an MIMO system with m-Tx antennas and n-Rx antennas. A received signal vector from -Rx antennas can be written into this form,
where y is the received signal vector and z is a noise vector and they both are with dimension n x 1, H is an MIMO channel matrix with dimension n x m , and x is an m x 1 column vector for m transmitted symbols. Given the received signal vector y and assuming the channel matrix H is known, our goal is to detect x . For the detection, we further assume the noise vector z is a white Gaussian with zero-mean and a normalized co-variance matrix E{zz^H} = I . For the cases where the noise vector is not white, i.e., the co-variance matrix E{zz^H} = Rzz , we then need to whiten the noise first by multiplying (Rzz)^(1/2) first to both sides of equation (1). We have,
Note that equation (2) is the same as equation (1) if we absorb the noise whitening matrix (Rzz)^(1/2) into the channel matrix H and consider the received signal vector and the noise vector are the ones after the noise whitening operation. Therefore, here, for the sake of simplicity, we assume the noise has been whitened and we use equation (1) to further explain how to detect (or estimate) the symbol vector x. Now, back to equation (1), to combine the received symbol replicas from multiple receive antennas, we often multiply H^H to both sides of the equation to yield,
It is interesting to note that the diagonal elements of the channel matrix (H^H H) combine the energy of each symbol replica from the receive antennas. To be specific, the k-th element of (H^H y) can be expressed into this form
where h_ij is the ij-th entry of the MIMO channel matrix H.
The first term at the right hand-side of the above equation is a combined energy of symbol replicas of x_k from all receive antennas, the second-term is actually interference, representing cross-talks from other symbols, and the third-term is for noise. Often, we do a further normalization by dividing the above by the gain
, where
Obviously, if there is no cross-talk, equation (4) means a maximal ratio combining to form a decision variable d_k for symbol x_k. If x_k is QAM symbol , we can estimate x_k by checking which QAM decision region that d_k falls into.
In the presence of cross-talks, the maximal ratio combining might not be a good detection approach for symbol x_k. We have heard of the zero-forcing approach, which basically tries to force the cross-talk to 0 by multiplying the inverse of (H^H H) to both sides of equation (3), i.e.,
For notational simplicity, we denote W = (H^H H)^-1 as the weighting matrix for the zero-forcing and we re-employ d = H^H y as the decision vector before the zero-forcing operation. Equation (5) can be rewritten as
and its k-th element can be expressed as
where
If we compare equation (7) and equation (4b), we can infer that the zero-forcing does some weighting and combining of decision variables d_j from other branches, i.e., (j <> k) , in order to remove the interference term I_k. That type of weighting and combining of decision variables obviously will bring noises from other branches into this k-th branch for symbol x_k. In other words, the noise component in Equation (7) will be larger than the noise component in (4b) as a result of forcing the interference term I_k in (4b) to 0 by combining the decision variables from other branches. Basically, if we use (4b) as the decision variable for symbol , we will suffer from the interference . If we zero-force the interference to 0 by using (7) as the decision variable, the resulting noise in (7) will be larger than the original noise in (4b).
|
||
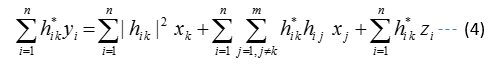
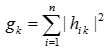 to yield a decision variable for symbol x_k . The decision variable can be written as
to yield a decision variable for symbol x_k . The decision variable can be written as