Communication Technology

Sampling Theory

As you start studying Signal Processing, one of the terminology that you come across the most frequently would be 'Sampling Theory' or 'Nyquist Sampling Rate', 'Over Sampling', 'Under Sampling' etc. I may sound easy, but do you really understanding the practical meaning of those words ? or the importance of them ?

I would not write down the dry definition of those terminologies. If you google it, you would easily find the dictionary type of definition.  In this page, I would take a rather intuitive / practical approach. The story will get very long and it would take long time for me to complete this page.. here goes just the beginning.

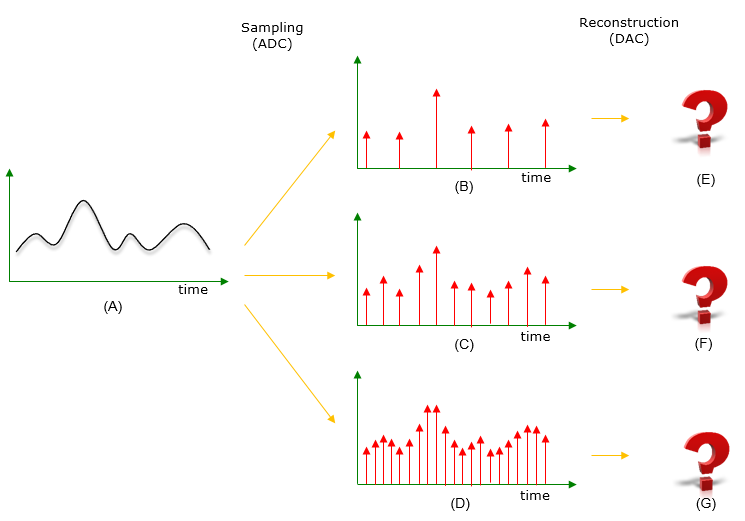
The first step in most Digital Signal Processing would be to sample analog signal and convert it into a digital form. Then the question is how often do we have to sample the original analog signal. Let's assume that we are given an analog signal as (A).  Now we are sampling the original signal (A) with the several different sampling rate as in (B), (C), (D). Then the question is "which (B,C,D) would best represent the original signal (A) ?'. In order words, if we convert the sampled signal (B, C, D) back to analog signal (E, F, G), which of E, F, G would be the closest (most similar) to the original signal (A) ?.

The answer would be simple and intuitive. You would easily pick (C) as the best answer.

Yes, you are right. The best answer is (C). You don't need to try to understand such a boring things like Sampling Theory.

Then what is the problem ? Just sample the signal at as high rate as possible.

It would be OK just to increase the sampling rate if you don't need to think of the cost and any other design limitation.

To sample the signal at high rate, you need high speed ADC and large memory capacity and various high processing power which is not always acceptable.

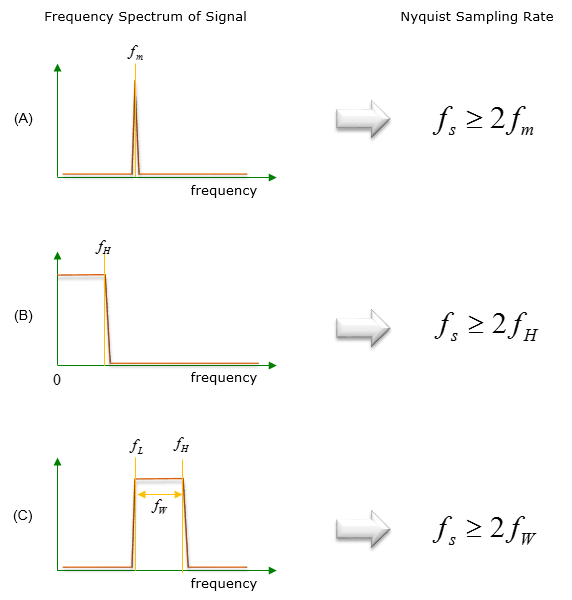
Now let's change a question a little bit as follows : What is the minimum sampling rate that would not lost any critical information of the original signal ?

There is where the Sampling Theory kicks in.

I will just give you the answer first. The minimum sampling rate that meets the requirement is called 'Nyquist Sampling Rate'. You would hear of this term over and over whenever you read any material about sampling theory.

The answer would be as illustrated below. As you see, the answer would take a little bit different form depending on the nature (frequency spectrum) of the original signal.

In case (A), the original signal has only one component with frequency fm. In this case, the Nyquist Sampling Rate is 2 times fm. So any sampling rate which is equal to or greater than twice of fm (2 x fm) would reserve all the critical information contained in the original signal.

In case (B), the original signal is made up of multiple frequency component starting from 0 frequency to fH. In this case, the Nyquist Sampling Rate is 2 times fH. So any sampling rate which is equal to or greater than twice of fH (2 x fH) would reserve all the critical information contained in the original signal.

In case (C), the original signal is made up of multiple frequency component, but starting frequency is not 0. It starts from fL frequency to fH. Let's denote the difference between fH and fL as fW(bandwidth of the signal). In this case, the Nyquist Sampling Rate is 2 times fW (Note that the Nyquist Sampling Rate is not 2 x fH). So any sampling rate which is equal to or greater than twice of fW (2 x fW) would reserve all the critical information contained in the original signal.

Then, you would have a question : What would happen if we sample the signal at lower rate than Nyquist Sampling Rate ?

This is a very important point of Sampling Theory and it would require pretty long explanation. The simple answer is 'Sampling at lower than Nyquist Rate would cause Aliasing'.

I know this would not make much sense to you if you are completely new to this area. I will post further details of this next time.   

Reference :

[1] SIMULATION OF DIGITAL COMMUNICATION SYSTEMS USING MATLAB By Mathuranathan Viswanathan

[2] USING MATLAB TO ILLUSTRATE THE' PHENOMENON OF ALIASING' by Sol Neeman, Johnson and Wales University

[3] EE 424 #1: Sampling and Reconstruction