Engineering Math - Differential Equation

Interest Model

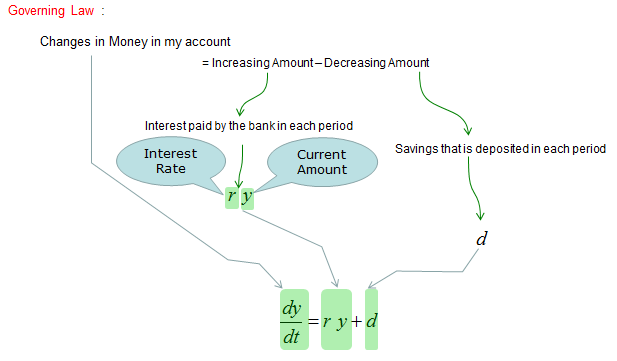
Let's assume that I want to model how much money I would have in my account in each period. Following equation describes how the money in your account changes over time

The left-hand side of the equation, dy/dt, represents the rate of change of the money in your account with respect to time. The right-hand side of the equation, ry + d, represents the sources of this change.

The first term, r * y, represents the amount of interest earned on your savings. The interest rate is multiplied by the amount of money in your account at each point in time, which gives you the amount of interest earned in that period. This implies that if you have more money in your account now, you will earn more money as interest which in turn will increase the amount of the money in your account.

The second term, d, represents the amount of money you deposit or save in each period. This increases the amount of money in your account and contributes to the rate of change of your savings. This is also intuitive. The more money you deposit, you will get more money in your account.

Overall, the equation captures how your savings grow over time with the combination of interest earned on the current balance and the additional savings you make each period. The solution to this differential equation would give you the function that describes the amount of money in your account as a function of time.

NOTE : You would notice that in this model you have only those factors increasing the money in your account. No factors descreasing the money in your account like expense. You may add those factors which would decrease the money in your account to make the model more realistic.