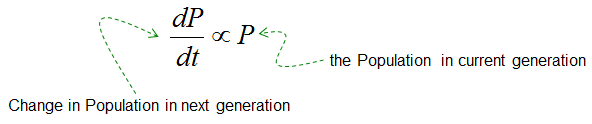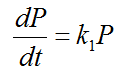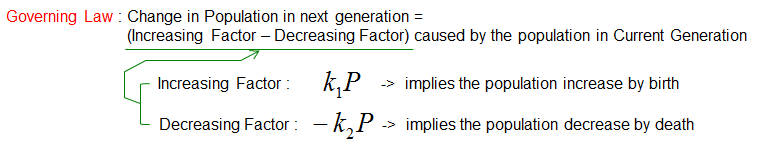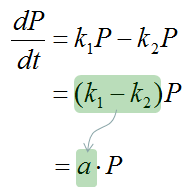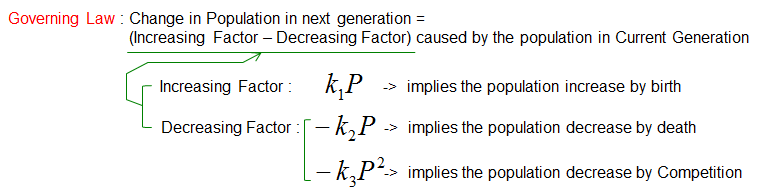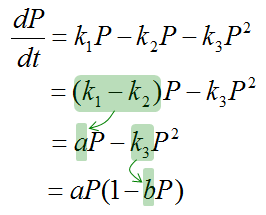This page will deal with how the population of a species would change over time. One thing you would notice from this page which may look a little bit different from physical models is about Governing Equation. In most of physical models, it would look obvious on why you have to use such an equation for the given model, but it may not look as such obvious in this kind of biological model. Most of the governing equation would be based on certain assumptions. If you change the assumption, you would have pretty different governing equation and as a result you will be end up with pretty different differential equation. So in case of biolological modeling, it is very important to understand clearly on what kind of assumptions are set for a specific case.

In physics, the governing equations often feel intuitive and readily apparent because they stem from well-established, fundamental laws. Take, for instance, Newton's laws of motion, which provide clear and direct relationships between force, mass, and acceleration, easily translated into mathematical equations.

However, when we shift our focus to biology, things become more intricate. Biological systems are inherently complex, with a multitude of interconnected factors influencing how living organisms behave and interact. This intricate web of relationships, involving things like birth rates, death rates, competition, and resource availability, makes it challenging to pinpoint precise mathematical connections. Unlike the seemingly straightforward laws of physics, the rules governing biological systems are often less obvious and more challenging to capture in simple mathematical terms.

In other words, Unlike physical models, which often have clear and intuitive reasons for the choice of their governing equations, biological models—such as population dynamics—may not initially seem as straightforward. This difference arises because biological systems are influenced by a wide array of complex, interdependent factors, making it less apparent why a specific equation is chosen to represent the system.

The governing equations in such models are typically derived based on a set of underlying assumptions about the biological system. These assumptions might include factors like constant birth and death rates, limited resources, predator-prey relationships, or environmental carrying capacity. However, if any of these assumptions change, the governing equation itself must also change to reflect the new conditions. Consequently, this leads to an entirely different differential equation describing the system's behavior.

For example, a simple population growth model might assume that the growth rate is proportional to the population size, leading to an exponential growth equation. However, introducing the concept of resource limitations would necessitate a modification to include a carrying capacity, resulting in a logistic growth equation. Similarly, incorporating predator-prey interactions or migration patterns could lead to even more complex models.

This highlights the critical importance of understanding the assumptions that underpin any biological model. The accuracy and applicability of a model rely heavily on these assumptions aligning with the real-world scenario being studied. When approaching biological modeling, it is essential to carefully analyze and define these assumptions, as they directly determine the structure of the differential equation and, ultimately, the insights the model can provide about the population dynamics of the species under consideration.

Population with No Death

The first case is the most simplest case. In this case, we assume that we see only a new birth of new individuals and there is no death in the population. Of course, there would be no such a case in real biological environment, but it would be beneficial to start with this ideal case since this is the simplest form and can be extendable to more realistic case just by adding some more factors (e.g, death, competition etc)

The concept of population modeling by starting with a simplified scenario: a population with no death.  It acknowledges that this is an idealized situation, unlikely to exist in reality, but argues that it's a useful starting point because of its simplicity. This basic model can then be expanded to incorporate more realistic factors like death, competition, and resource limitations.

The Governing Law in this case can be described as below.

If you convert the governing law into mathematical form as it is, it can be represented as shown below. (You may ask why the 'Change in Population' is proportional to P, not to P^2 nor P^3 etc. Your question is valid.. you can try with your imagination and check if your model can explain a real data)

The core principle of this simplified model is that the change in population size over a generation is directly proportional to the current population size. In simpler terms, the bigger the population, the more newborns there will be, leading to a larger increase in the next generation. This relationship is expressed mathematically as dP/dt ∝ P, where dP/dt represents the change in population over time, and P represents the current population.

If we introduce a proportional constant (let's call it k1), you can come out with an equation as shown below.

This implies that the growth rate depends directly on the current population. The larger the population, the greater the number of new individuals added in the next generation. This relationship reflects the concept of exponential growth, where the population grows faster as it increases in size.

NOTE : Why is the change in population proportional to P, and not to P squared or P cubed? It suggests that readers can explore this question through thought experiments and by comparing different models to real-world data.

You may wonder why the growth rate is proportional to P and not P², P³, or some other power of P. This question is valid and invites exploration. You can test these alternate assumptions and compare their results to real-world data to understand why this simple proportional relationship often works well as a first approximation.

Solution to this equation

This differential equation can be solved analytically, but you may skip this part if you are really allergic to math. If you are just a little bit of interest in the math, you may refer to this note before you continue to read :

To solve the differential equation dP/dt = k₁P, we start by separating the variables:

dP/P = k₁ dt

Integrating both sides gives:

∫ (1/P) dP = ∫ k₁ dt

The solution to these integrals is:

ln|P| = k₁t + C

Exponentiating both sides to remove the natural logarithm yields:

|P| = e^{k₁t + C}

Let e^C be a constant C₁. Thus:

P(t) = C₁ e^k₁t

If the initial population at t = 0 is P₀, substituting this condition gives:

P(0) = C₁ e^k₁(0) = C₁

Therefore, C₁ = P₀, and the final solution is:

P(t) = P₀ e^k₁t

This solution describes exponential growth if k₁ > 0 or exponential decay if k₁ < 0.

Imagine you're watching a colony of bacteria grow. At the very beginning, you have a certain number of bacteria, let's call that P₀.

Now, this equation, P(t) = P₀ e^k₁t, is like a magic formula that tells you how many bacteria you'll have after a certain amount of time (that's what the "t" stands for).

The "e" and "k₁" in the equation are a bit tricky, but think of them as special ingredients that control how fast the bacteria multiply.

• If k₁ is a positive number, it means the bacteria are multiplying and growing really fast – like when you leave food out for too long! This is called exponential growth. The bigger k₁ is, the faster the growth.
• But if k₁ is negative, it's the opposite. Imagine you added some antibacterial soap – the bacteria would start to disappear! This is exponential decay. The more negative k₁ is, the faster they vanish.

So, this equation is a simple way to describe how things can grow or shrink incredibly fast over time. It's like a super-powered multiplication or division problem!

Population with Death with Natural Cause

Now let's extend the previous model one step further to make it more realistic. In this mode, I would add one factor that would cause the decrease of the population. What would be the most common cause to decrease the population ? You know that there is no life that live forever. It would die off some time. so it would be natural to add the factor of death with natural cause (implying 'dying of age').

Model expansion

In this section, we build upon the simple population model by adding the concept of death due to natural causes. In real life, no population lives forever—individuals eventually die due to aging, disease, or other factors. To reflect this, we modify the governing law to include both the increase in population due to births and the decrease in population due to deaths.

If we add this factor, the governing law can be as follows.

Increasing Factor: The population grows due to births, which is proportional to the current population P. This is represented mathematically as k₁P, where k₁ is the birth rate constant. It measures how quickly the population grows due to births.

Decreasing Factor: The population decreases due to deaths, which is also proportional to the current population P. This is represented mathematically as k₂P, where k₂ is the death rate constant. It measures how quickly individuals die off naturally.

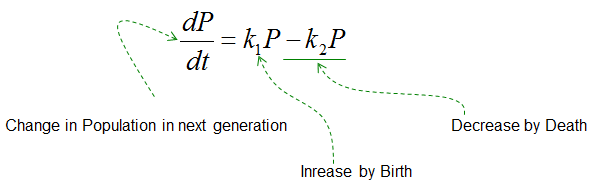
If you just convert the Governing Law into mathematical form you would get the following equation. (You may ask the similar question as before, like 'why Death is proportional to P, not P^2, P^3 etc. Would the 'Decrease by Death' change if the cause of death changes ? like death by other factors like desease or epidemics ?. Very good questions. Think about it)

Here:

• dP/dt is the rate of change of the population.
• k₁P represents the increase in population due to births.
• k₂P represents the decrease in population due to deaths.

Simplified Form

I prefer to write the equation as above because you can understand the meaning of each terms more easily (almost intuitively). But many textbooks tend to write the equation in simplified form as below. Since both terms are proportional to P, we can combine the constants k₁ and k₂ into a single constant a, which represents the net growth rate: In this case, it is important that the meaning of 'a' is the combination of two factors, i.e, net factors of birth and death.

In this simplified form:

• If a > 0, the population grows because births outweigh deaths.
• If a < 0, the population shrinks because deaths outweigh births.
• If a = 0, the population remains constant, meaning births and deaths are balanced.

Solution to this equation

This differential equation can be solved analytically, but you may skip this part if you are really allergic to math. If you are just a little bit of interest in the math, you may refer to this note before you continue to read :

This is a first-order linear differential equation. Using the separation of variables method:

dP/P = a dt

Integrate both sides:

∫(1/P) dP = ∫a dt

This results in:

ln|P| = at + C

Exponentiate both sides to solve for P:

P = e^C · e^at

Let e^C = C₁ (a positive constant). The solution becomes:

P(t) = C₁ e^at

Solution with Initial Condition

Suppose the initial population at time t = 0 is P₀. Substituting t = 0 and P(0) = P₀:

P(0) = C₁ e^{a · 0} = C₁

This implies C₁ = P₀. The final solution is:

P(t) = P₀ e^at

Interpretation of the Solution

The solution P(t) = P₀ e^at describes how the population changes over time:

• When a > 0:
  The birth rate is higher than the death rate (k₁ > k₂). The population grows exponentially. For example, if a = 0.1, the population grows faster as time increases.
• When a < 0:
  The death rate is higher than the birth rate (k₁ < k₂). The population decreases exponentially (decays). For example, if a = -0.1, the population shrinks rapidly at first, then slowly approaches zero.
• When a = 0:
  The birth rate equals the death rate (k₁ = k₂). The population remains constant: P(t) = P₀.

Applications of the Solution

This model can be used in various scenarios:

• Exponential Growth: Predicting populations with abundant resources and no constraints (e.g., bacterial growth in a lab).
• Exponential Decay: Modeling declining populations due to high death rates or resource shortages (e.g., endangered species).
• Stable Populations: Representing populations in balance, where births equal deaths (e.g., certain long-term ecosystems).

Extensions of the Model

This model assumes that the birth and death rates (k₁ and k₂) are constant. For more realistic scenarios, additional factors can be included, such as:

• Carrying capacity: Introducing a limit to growth leads to the logistic growth model.
• Inter-species interactions: Predator-prey or competitive models can be developed.

Thought Exercise

You might wonder why deaths are modeled as proportional to P rather than P², P³, or some other function of P. This is because, in most cases, the number of deaths is directly linked to the size of the population. However, for more complex situations—such as epidemics where deaths depend on population density—this assumption might need to be modified.

Practical Implications

This extended model is more realistic than the basic exponential growth model. It acknowledges that populations are affected by both birth and death processes. Such models can be used to:

• Predict the growth or decline of a species under natural conditions.
• Estimate how factors like aging or disease impact population dynamics.
• Serve as a starting point for even more complex models, such as those that include competition, resource limitations, or immigration.

Conclusion

This modification adds realism to the population model by introducing deaths into the equation. However, it still assumes that birth and death rates are constant and proportional to the population size. Future extensions can incorporate varying birth and death rates to reflect environmental changes, diseases, or other dynamic factors.

Population with Death with Natural Cause and Competition

Now let's extend the previous model one step further. I would add another decreasing factor : Decreasing by Competition.

In this model, we extend the population dynamics further by adding another realistic factor: competition. Competition introduces a new way for the population to decrease. It reflects the natural limitations that occur when individuals of the same species compete for limited resources such as food, space, or mates.

This adjustment makes the model more realistic, as it accounts not only for births and natural deaths but also for the effects of overcrowding and competition.

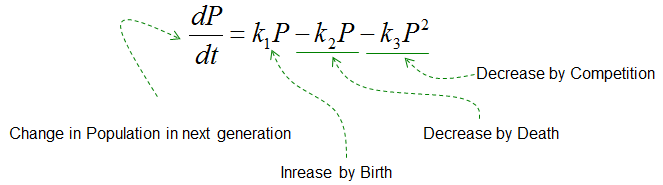
If you just convert the Governing Law into mathematical form you would get the following equation. (You may ask the similar question as before, like 'why Competition is proportional to P^2, not P, P^3 etc.  Very good questions. Think about it. Some people say 'Competition is modeled as proportional to P^2 since normally competition usually happens when two individual encounter each other'. But it is also possible for you to come out with other competition model as well)

Increasing Factor:

• Births: The population grows due to reproduction. This is proportional to the current population size P, represented mathematically as k₁P, where k₁ is the birth rate constant.

Decreasing Factors:

• Deaths: The population decreases due to natural causes (e.g., aging, disease). This is proportional to P, represented as k₂P, where k₂ is the death rate constant.
• Competition: The population decreases further due to competition for limited resources. This effect is proportional to P², represented as k₃P², where k₃ is the competition rate constant. Competition is modeled as proportional to P² because it increases with the likelihood of interactions between individuals, which depends on population density.

Here:

• k₁P: Increase in population due to births.
• k₂P: Decrease in population due to natural deaths.
• k₃P²: Decrease in population due to competition.

Simplified Form

Again, I prefer to write the equation as above because you can understand the meaning of each terms more easily (almost intuitively). But many textbooks tend to write the equation in simplified form as below.

Let's look into the simplication process in more details:

Factor P from the first two terms:

dP/dt = P(k₁ - k₂) - k₃P²

Define a = k₁ - k₂, which represents the net growth rate (the balance of births and deaths):

dP/dt = aP - k₃P²

To simplify further, let b = k₃ (competition constant), giving:

dP/dt = aP(1 - bP)

NOTE : Why Competition is Proportional to P²

It is because it depends on interactions between individuals. If each individual can potentially interact with every other individual, the number of interactions scales with P² .  In other words,  you need to find the practical mening of P² from P * P which indicates the interaction of two individuals. This is a reasonable first approximation for many natural populations, though other functional forms might be used in specific cases.

Interpretation of the Equation

The simplified form dP/dt = aP(1 - bP) is a logistic equation that describes how population changes over time under the influence of both growth and competition. Let’s break this down:

• When the population is small (P ≈ 0):
  • The term 1 - bP is approximately 1, so the equation reduces to dP/dt ≈ aP.
  • This means the population grows approximately exponentially, as competition has little effect when the population is small.
• When the population increases (P grows):
  • The term bP becomes significant, reducing 1 - bP.
  • Growth slows down due to competition as the population approaches the limit defined by the carrying capacity.
• When the population reaches a critical size (P = 1/b):
  • 1 - bP = 0, so dP/dt = 0.
  • This means the population stabilizes, as births balance out deaths and competition. This stable population size is called the carrying capacity.
• If the population exceeds the carrying capacity (P > 1/b):
  • The term 1 - bP becomes negative, causing the population to decrease.
  • This represents overpopulation where competition causes the population to shrink back toward the carrying capacity.
   

Solution of the Equation

This differential equation can be solved analytically, but you may skip this part if you are really allergic to math. If you are just a little bit of interest in the math, you may refer to this note before you continue to read :

The equation we are solving is:

dP/dt = aP(1 - bP)

This is the logistic growth equation, which models population growth that slows and stabilizes due to competition or resource limitations. Below is the solution step by step.

Separate the Variables

Start by rearranging the terms to separate P and t:

1 / P(1 - bP) dP = a dt

Simplify the Left-Hand Side

Using partial fraction decomposition, we simplify:

1 / P(1 - bP) = 1 / P + 1 / [b(1 - bP)]

The equation becomes:

(1 / P + 1 / b(1 - bP)) dP = a dt

Integrate Both Sides

Left-Hand Side:

• ∫(1 / P) dP = ln|P|
• ∫(1 / (1 - bP)) dP = -1/b ln|1 - bP|

Combining these results:

ln|P| - 1/b ln|1 - bP|

Right-Hand Side:

∫a dt = at + C

Combine and Simplify

The equation becomes:

ln|P| - 1/b ln|1 - bP| = at + C

Exponentiating both sides to solve for P:

P / (1 - bP)^1/b = e^{at + C}

Let e^C = C₁, so:

P / (1 - bP)^1/b = C₁e^at

Solve for P

Rearranging to isolate P gives:

P(t) = C₁e^at / (1 + bC₁e^at)

Substituting the initial condition (P(0) = P₀), we find:

P(t) = P₀e^at / (1 + bP₀e^at)

Behavior of the Solution

• When t → 0:
  P(t) ≈ P₀ (the population starts at its initial value).
• When t → ∞:
  The population stabilizes at the carrying capacity, P(t) → 1/b.
• When P « 1/b:
  Growth is approximately exponential: P(t) ≈ P₀e^at.
• When P ≈ 1/b:
  Growth slows down, and the population stabilizes at the carrying capacity.

Key Insights

• Carrying Capacity (1/b): The population stabilizes at this size due to resource limitations and competition.
• S-Curve Behavior: The logistic model predicts an S-shaped growth curve with exponential growth at first, slowing due to competition, and stabilizing at the carrying capacity.

Applications of the Logistic Population Model

The logistic equation, dP/dt = aP(1 - bP), is widely used in understanding real-world population dynamics. Below are some practical scenarios where this model proves valuable:

• Stable Ecosystems
• Explanation: In natural ecosystems, populations often stabilize at a specific size known as the carrying capacity. This happens because of limited resources like food, water, and shelter. The logistic equation models this behavior, showing how populations grow rapidly when resources are plentiful, then slow down and stabilize as they reach the environment's capacity to support them.
• Example: A population of deer in a forest will initially grow quickly when resources like food and water are abundant. However, as the population grows, competition for these resources increases, slowing down growth until the population stabilizes around the forest's carrying capacity.
• Overcrowding Effects
• Explanation:The logistic model incorporates competition through the term bP², which represents the effect of overcrowding. When populations become too large, competition for limited resources intensifies, leading to a decline in growth rates. If the population exceeds the carrying capacity, the model predicts a reduction in population size as resources become insufficient to sustain the excess individuals.
• Example:In a small pond, a fish population may grow quickly at first. However, as the population becomes too dense, food and oxygen levels drop, leading to increased competition. This can slow growth or even cause a population decline as weaker individuals cannot survive.
• Resource Management
• Explanation:By understanding the concept of carrying capacity, wildlife managers and conservationists can make informed decisions to ensure sustainable populations. They can use the logistic model to predict how populations will respond to changes in resources, habitat size, or other factors, allowing them to implement policies to maintain ecological balance.
• Example:Conservation programs for endangered species, like tigers, use this model to estimate the maximum number of animals a protected area can support. Based on these estimates, measures such as habitat restoration or controlled breeding programs can be implemented to keep populations stable and prevent overpopulation or extinction.
• Human Population Growth
• Explanation:While the logistic equation is often used for animal populations, it can also model human population growth in specific regions. As resources like arable land and water become limited, growth rates slow down, approaching the carrying capacity of the environment.
• Example:In rapidly urbanizing areas, population growth initially surges due to better living conditions and medical care. However, as cities reach their limits for housing, water, and infrastructure, growth rates slow, stabilizing the population.
• Agricultural Planning
• Explanation: Farmers and agricultural planners use logistic models to predict the growth of crops or livestock populations. These predictions help in managing resources like land, water, and fertilizers efficiently to ensure maximum yield without overexploitation.
• Example: A farmer raising cattle may use the logistic equation to determine how many animals can be supported by the available pasture without degrading the land's quality over time.
• Pest Control
• Explanation : The model is also useful for controlling pest populations. Understanding how pests grow and stabilize at a carrying capacity can help in designing strategies to keep their numbers in check.
• Example: In agriculture, logistic models can predict how a pest population will grow if left unchecked and how interventions like pesticides or natural predators can prevent the population from exceeding a harmful threshold.