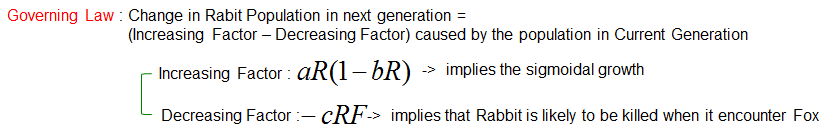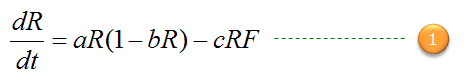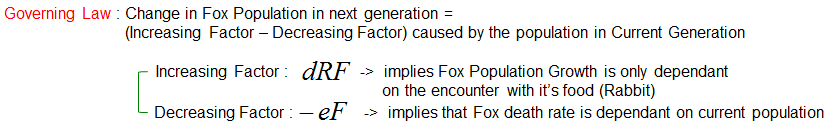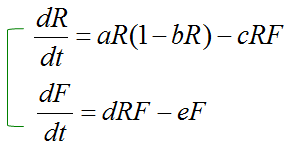|
|
||
|
The prey and predator model offers a fascinating lens to understand the intricate balance of ecosystems, where survival is a constant interplay of growth and decline. At its core, this model reflects how populations of two species—such as rabbits and foxes—are not just interdependent but dynamically influence each other over time. While intuition might suggest simple cause-and-effect relationships, like more predators leading to fewer prey, the reality is far more nuanced. The feedback loop inherent in this interaction—where predator populations depend on prey abundance, and prey populations are controlled by predation—creates oscillations rather than straightforward outcomes. For instance, a temporary abundance of rabbits might fuel a rise in fox populations, but as prey becomes scarce, predators face resource shortages, triggering their decline. This cyclical pattern is a hallmark of predator-prey dynamics, rooted not just in hunting behaviors but also in environmental factors, reproductive rates, and even chance events. Mathematical models like the Lotka-Volterra equations help untangle these complexities by providing tools to predict when populations stabilize, peak, or crash. These models reveal that what seems chaotic at first glance is governed by underlying principles—principles that can illuminate broader ecological and even societal systems where resources and consumers are in flux. Let's approach with intuitionLet's start with an Intuitive approach. Let's assume that you are oberving a Rabit population and Fox population in an area. And by common sense and observation, you would know Fox hunts Rabits meaning Fox is the predator and Rabit is the prey in the area. Without using any math and just using your intuition, think of what would happen if the number of Fox would increase in the area ? You may easily think that the number of Rabit will decrease because more and more rabbits will be killed by Fox. It is easy. Then, will all the rabit will be eaten by Fox and they will completely disappear ? The answer to this question is not easy. The answer can be 'Maybe Yes, Maybe No. The answer would depend on the population changes of Fox and how fast the fox eats away rabits etc. To get the answer to this kind of tricky question you need to use mathematical modeling and understand the exact relationship between the two populations. Again only using your intuition, think of what will happen when the birth rate of Rabit increases and the number of Rabit increases ? You may easily guess that the number of Fox will increase as well because they get food more easily. Then, will this situation goes forever ? Will fox hunt rabit such easily forever ? Probably not, because as fox hunt rabit more easily and the number of fox increases, at some point the number of rabit may decrease since too many rabits are hunted. Decreasing number of rabbit means decreasing food for Fox and eventually the number of Fox will decrease as well. Now you may roughly understand the inter-relationship between Rabbit population and Fox population. But if I ask you about exactly when the rabbit popuation would grow or shrink or exactly when the fox popuation would grow or shrink. You cannot answer this questions without exact mathematical modeling of those population changes. In this note, we will derive very basic models of these population changes using differential equation. How Rabbit Population Changes ?First let's think of the rule (Governing Law) for the population change of the rabit. It can be described as follows.
Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the rabbit as follows.
This equation represents the delicate balance of growth and decline in a rabbit population, governed by natural reproduction, environmental constraints, and predation by foxes. The first term,
The change in the rabbit population (
How Fox Population Changes ?Now let's think of the rule (Governing Law) for the population change of the fox. It can be described as follows.
Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the fox as follows.
The rate of change of the fox population (dF/dt) is determined by:
This equation demonstrates that the fox population dynamics are primarily influenced by two elements: the availability of prey (which fuels growth) and the natural death rate (which causes decline). When prey is abundant, the first term (
Putting Them TogetherNow you have a two equations for rabbit and fox population. However, you cannot solve the two equation separately because Rabbit population equation has fox population as a part of the equation and Fox population equation has rabbit population as a part of the equation. To get the solution for the two equation, you have to combine the two into a system equation (simultaneous equation) as show below and solve the system equation. For now, don't worry about solving the proplem. If you just understand the meaning of this equation, my goal is done. I will give you a graphical solution for this equation later.
By combining the two equations, this model captures the interwoven relationship between predators and prey. It provides a framework for understanding how ecological systems balance growth, decline, and interdependence. This foundation can be expanded to include additional complexities, such as external factors (e.g., seasonal changes, environmental disruptions) or multi-species interactions, making it a versatile tool in ecological modeling and conservation efforts. The System of EquationsdR/dt = aR(1 - bR) - cRF This equation describes the rate of change in the rabbit population (
dF/dt = dRF - eF
This equation models the fox population ( Interdependence of the Equations
These two equations are deeply interconnected:
- The rabbit population equation ( Thus, the behavior of one population cannot be isolated from the other. To predict how both populations will evolve over time, the equations must be solved together as a system. Solving the SystemTo find a solution, the equations must be solved simultaneously. This involves:
Dynamic Behavior and InsightsThe dynamic behavior of the predator-prey system is characterized by a fascinating interplay of growth and decline that results in cyclical population patterns. This oscillatory behavior emerges naturally from the interactions between the rabbit and fox populations: an abundance of rabbits provides more food for foxes, causing their numbers to rise. However, as the fox population grows, predation intensifies, leading to a decline in the rabbit population. With fewer rabbits available, the fox population eventually decreases due to food scarcity, allowing the rabbit population to recover and restart the cycle. Beyond these oscillations, the system can also reach equilibrium points where both populations stabilize, though the stability of these points depends heavily on the initial conditions and parameters, such as predation efficiency and mortality rates. Small changes in these parameters can have profound effects, potentially destabilizing the system and leading to outcomes like population collapse or unchecked growth. This sensitivity to parameters highlights the delicate balance that governs the predator-prey relationship.
|
||