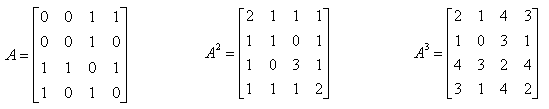Engineering Math - Graph Theory

  

 

 

 

Adjacency Matrix

 

Adjacency Matrix is a matrix which describes the connectivity among the nodes in a graph. (Google "Introduction to Graph Theory" or "Graph Theory Tutorial" if you are new to this area). The way you can construct the Adjacency Matrix from a graph is as follows. I hope this illustrations gives you the intuitive understanding without much description.  Basic idea is to put "1" at the matrix element representing two points (from, to) if there is a connection for the two points and put "0" otherwise.

 

 

 

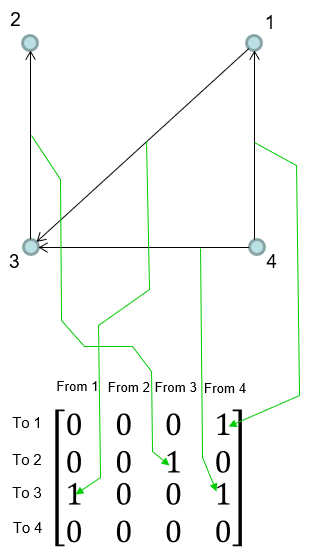
Adjacency Matrix for Directed Graph

 

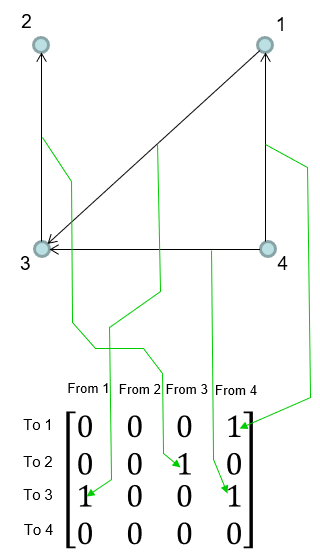
Adjacency Matrix is a matrix that represents the connection among vertices. There can be two ways of representing the connection in matrix as in < Case 1 > and < Case 2 >. I think the typical way is < Case 1 > but < Case 2 > is also possible as long as you use the notation consistently in all the equations in which the matrix is used.

 

< Case 1 >

 

 

< Case 2 >

 

 

 

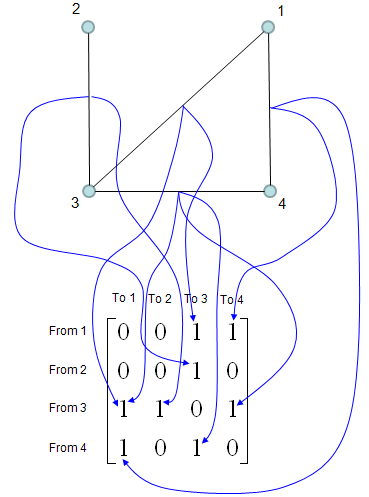
Adjacency Matrix for Non-Directed Graph

 

 

 

Once you have the Adjacecy Matrix, you can do a lot of mathemtical operation for the matrix to find various useful information.

 

 

 

Properties of Adjacency Matrix

 

  • Even with the same graph, if lebeling (index) for each vertex is different, you may have different Adjacency Matrix. But the eigenvalues of all the adjacency matrix for the same graph is always same.
  • If the eigenvalues of two graphs do not match (are not same), then the graphs are not isomorphic. (But the converse is not true, meaning that there are cases where two graphs are not isomorphic but they have the same eigenvalues).
  • If all of the eigenvalues of an adjacent matrix is real value, it means the adjacency matrix is symetric.
  • If the adjacency matrix is symetric, it means that the graph is undirected.
  • If the adjacency matrix is symetric, all of the eigenvectors of the matrix is orthogonal to each other.

 

 

 

Application : Seeking connected path among vertice

 

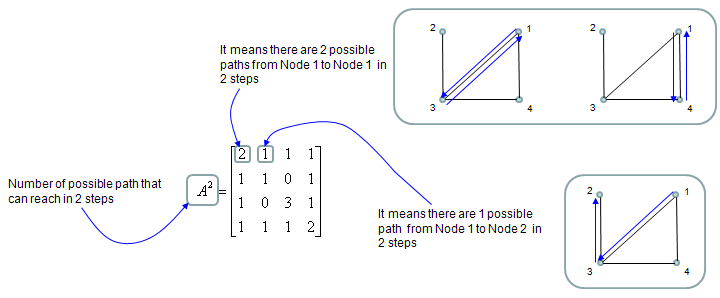
The most common mathematical operation for the Adjacent Matrix is to take "Powers of the matrix". Following shows three matrix, A which is original adjacency Matrix and A^2 and A^3.

 

 

Element value in A^2 is the number of possible paths connecting the two nodes represented by the element. If an element value is "1", it means there is only one path from one node to the other node that is represented by the element. If an element value is "2", it means there are two possible paths from one node to the other node that is represented by the element as illustrated below. In most case, only those elements with the value of "1" has practical meaning.

 

 

Examples on YouTube