A neural network looks complicated when you draw every connection. But the calculation at each layer is one simple operation repeated many times: multiply each input by a weight and add the products up. This page shows how that "Sum of Times" operation turns into a single matrix equation for a whole layer. I'll start with the network itself, then compute the input to one node, then write the matrix form, and finally look at what the network does with the result.

• What does the network in this example look like ?
• How is the total input to one node calculated ?
• How does one matrix equation cover a whole layer ?
• What happens after the matrix product ?

What does the network in this example look like ?

Before writing any equation, let's count what the drawing contains. The number of nodes in each layer decides the size of every matrix on this page, so this count comes first.

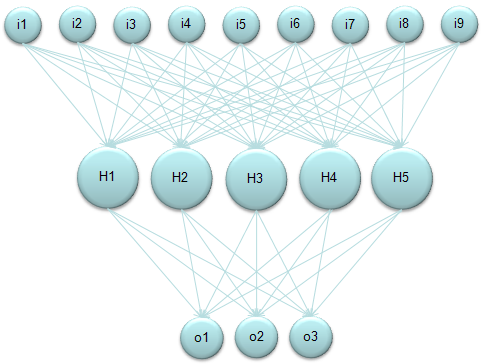
One of the most wildly used form of Neural Network would be illustrated as follows. Here in this diagram,

"i" stands for input layer

"H" stands for hidden layer

"o" stands for output layer

I am not going to explain what is meaning (role) of these components. Please try google "Neural Network Tutorial" or "Introduction to Neural Network" if you are new to this area.

The drawing above has nine input nodes, i1 to i9, five hidden nodes, H1 to H5, and three output nodes, o1 to o3. Every input node has an arrow to every hidden node, and every hidden node has an arrow to every output node. A network wired this way is called fully connected.

• Between the input layer and the hidden layer there are 9 x 5 = 45 arrows. Each arrow carries its own weight.
• Between the hidden layer and the output layer there are 5 x 3 = 15 arrows, so 15 more weights.
• The arrows only go downward in the drawing. No node sends a value back to an earlier layer or to a node in its own layer. So the calculation runs one layer at a time, from the top to the bottom.

• The layer sizes set the matrix sizes : nine inputs and five hidden nodes give a 5 x 9 weight matrix, and five hidden nodes and three outputs give a 3 x 5 matrix.
• Every arrow is one weight : this network has 45 + 15 = 60 weights, and training a network means finding good values for all of them.

How is the total input to one node calculated ?

Every node in the drawing does the same arithmetic on the values that reach it. Let us follow it for one node, H1, before dealing with a whole layer. The four steps below give the recipe, and the equation after them writes the recipe in one line.

But the basic calculation logic as as follow.

i) Take a Node (a Circle, for example H1).

ii) Take all the input value (each arrow) getting into it.

iii) Take all the weight value which is associated with each of the input value.

iv) Multiply each input value with its corresponding weight value and take the sum of all the multiplication (This is "Sum of Times" process). This become the total input value to the selected Node.

The total input to H1 depends on nine values and nine weights. Let's write it with explicit indices, because the index convention decides how the matrix in the next section is laid out.

I'll write w_jk for the weight on the arrow from input node j to hidden node k. The first index is the source and the second index is the destination. With this convention, the four steps above give the following sum for H1.

total input to H1 = w11i1 + w21i2 + w31i3 + ... + w91i9

Only the first index changes along the sum, because all nine arrows end at the same node H1. For H2 the second index becomes 2, and the sum uses w₁₂ to w₉₂. Here is a small example. Let the inputs be (1, 0, 1, 0, 1, 0, 1, 0, 1), and let w₁₁ to w₉₁ be 0.1, 0.2, ... 0.9. Only the odd-numbered inputs are nonzero, so the total input to H1 is 0.1 + 0.3 + 0.5 + 0.7 + 0.9 = 2.5.

• One node needs one sum of nine products : the total input is a weighted sum, which is the same thing as the dot product of the weight vector and the input vector.
• The index order matters : in w_jk the first index is the input node and the second is the node that receives the value. The matrix layout below depends on this choice.

How does one matrix equation cover a whole layer ?

Five hidden nodes need five sums like the one above. Writing them one by one works, but it hides the structure. Stacking the five weight vectors as rows of one matrix shows the whole layer in one line, and it is also the form that software uses.

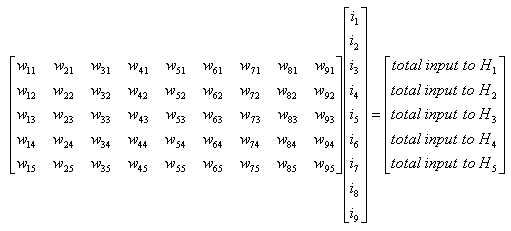
If you do this process for only a single Node (e.g, H1), you can represent it as simple "Sum of Times" form. But if you want to describe this process for all the Nodes at each layer (e.g, H1, H2, H3, H4, H5) it would be easier/clearer to represent it as a Matrix equation as follows. (Of course you can represent this into five separate "Sum of Times/Sum of Multiplication" form, but Matrix form would neat clearer).

Let's read the matrix above row by row. Row k holds the nine weights that end at hidden node H_k. So row 1 is w₁₁, w₂₁, ... w₉₁, which is exactly the sum written for H1 in the previous section. Multiplying row k by the input column gives the total input to H_k.

The matrix has 5 rows and 9 columns, and the input vector has 9 entries. So the product has 5 entries, one for each hidden node. If you store the weights in a 9 x 5 table W instead, with w_jk in row j and column k, then the matrix above is its transpose W^T. Both layouts appear in textbooks and libraries. So check the shape of the weight matrix before you reuse a formula from another source.

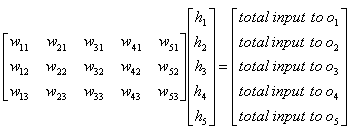
With the same logic as described above, you can get the matrix equation to calculate the total input to the layer 'o (output)'.

The output layer uses the same pattern with smaller sizes. The matrix above has 3 rows and 5 columns, and it multiplies the five values h₁ to h₅ that leave the hidden nodes. Its weights are a second, separate set. They reuse the names w₁₁ to w₅₃, but they belong to the arrows between the hidden layer and the output layer.

Notice one mistake in the drawing. A 3 x 5 matrix times a 5-entry vector gives 3 entries, and the network has only three output nodes. So the right-hand side should stop at the total input to o₃. The rows for o₄ and o₅ do not exist.

• One row per receiving node : each row of the weight matrix holds the weights of all arrows that end at one node.
• The shapes must match : a 5 x 9 matrix needs a 9-entry input and gives 5 results. A 3 x 5 matrix needs 5 entries and gives 3.
• Each layer has its own weight matrix : this network needs a 5 x 9 matrix and a 3 x 5 matrix, even when both use the same w names.

What happens after the matrix product ?

The matrix product gives the total input to each node, but it is not yet the output of the node. Two more pieces complete a real network: an activation function and a bias. Let's add them and see why the first one is essential.

Each node passes its total input through an activation function f. A common choice is the sigmoid, f(x) = 1/(1 + e^-x), which maps any number into the range 0 to 1. So the value leaving hidden node k is h_k = f(total input to H_k). These h_k values are the inputs of the output layer in the second matrix equation.

Why not skip f? Without it, the two layers collapse into one. The hidden result is W₁i, and the output is W₂(W₁i) = (W₂W₁)i. The product W₂W₁ is just another 3 x 9 matrix, so the hidden layer adds nothing. The nonlinear f is what lets a deeper network represent more than a single matrix can.

Most networks also add a bias b_k to each node, so the total input becomes Wi + b. You can keep the pure matrix form by appending a constant 1 to the input vector and a bias column to the matrix. The hidden-layer matrix then becomes 5 x 10. With one bias per hidden and output node, the network of this page has 60 weights and 5 + 3 = 8 biases.

The matrix form also helps when you process many inputs at once. Put N input vectors side by side as the columns of a 9 x N matrix. One product with the 5 x 9 weight matrix then gives a 5 x N matrix, which holds the total inputs of all hidden nodes for all N samples.

hidden layer : h = f(W1i + b1)    W1 : 5 x 9,  i : 9 x 1,  h : 5 x 1
output layer : o = f(W2h + b2)    W2 : 3 x 5,  h : 5 x 1,  o : 3 x 1

• A layer is a matrix product followed by a function : the matrix gives the total inputs, and f turns them into node outputs.
• The activation function keeps the layers separate : without it, any stack of layers reduces to one matrix.
• A bias fits into the matrix form : a constant 1 at the end of the input vector turns Wi + b into one product.
• Batches become matrix-matrix products : N inputs stacked as columns are processed by one multiplication.