Communication Technology

  

 

 

 

Channel Capacity/Shannon's Law

 

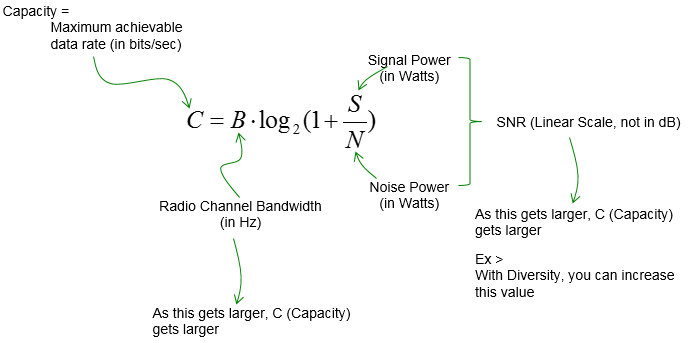
One of the most important goals for the engineers designing a communication system is to achieve the highest data rate with as low as possible resource allocation (e.g, spectrum allocation). However, you can easily guess that there would be some physical limit however good/fancy technology you use. Then, the question is 'how can we figure out the physical limit of the achievable data throughput in a given condition ?'.

Shannon's Law (or Shannon-Hartly equation) is the equation (theory) to answer this question. The equation shows as follows. If you just verbablize (express in words) this equation, you will get a lot of practical information.

 

 

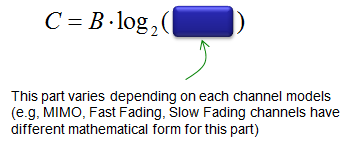
Depending on the implementation and various conditions during the communication, the terms in the log () term would vary as mentioned below.

 

 

Now let's convert this equation into words. Just try to interpret this equation into your own words before you read the followings. This kind of practice (converting a mathemtical equation into words and vice versa is very important practice in engineering).

  • Maximum Capacity (Maximum throughput) achievable is determined by Bandwidth(B) and SNR of the communication channel, Singal Power and Noise Power

  • The capacity is directly proportional to the channel bandwidth. It implies that you can infinately increase the capacity if you can increase bandwidth infinitely. ==> In theory it is true, but there are a lot of practical issues and difficulties of increasing the bandwidth increasingy.

  • With a given Bandwidth, Maximum capacity increases as SNR (signal to noise ratio) increases. ==> But there is one thing you should notice. Since SNR is in log() function, the rate it increases decreases as SNR increases. It mean in relatively low SNR, SNR improvement impact a lot but in very good SNR, beter SNR does not play much role in increasing the capapcity. You would notice this from log plot that you learned from high school.

  • If we assume that SNR stay same, Maximum capacity increases as Channel Bandwidth increases.

  • If we assume the Bandwidth is fixed and Noise Level stay same, the Maximum Capacity increase as Signal Power increases.

  • If we assume the Bandwidth is fixed and Signal Power stay same, the Maximum Capacity increases as Noise Level decreases.

  • (This is unrealistic, but ) if Noise Level goes to Zero, we can achieve Infinite Capacity (This is possible only in mathemtical sense. It cannot be achievable in reality because it is impossible to achieve Zero noise in reality)

 

In case of MIMO, we may expand the equation as follows. Interpretation is simple. Channel Capacity is directly proportional to the number of MIMO channel meaning we can indefinately increase channel capacity by increasying the number of MIMO streams (layers) infinately. But practically it would be more and more difficult to increase the number of MIMO streams.