Engineering Math - Matrix

Column Selection Vector

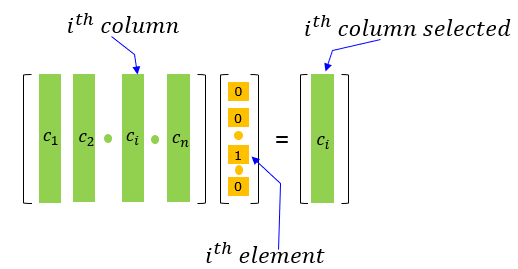
I don't know how important this is in terms of pure mathematics, but I want to introduce this concept since it is useful in some cases.

When a matrix is multiplicated with a vector as shown in the following way, the non-zero item in the multiplication function as a tool that is selecting a specific column from the matrix. It can be proved easily just by calculating the inner product of the matrix and vector by hands. If you interpret the vector as a column selector, you can easily figure out the multiplication of a matrix and vector in this form without going through the complicated process of inner product.

You can clearly understand how this column selection vector works just by trying a few examples as below.

Example 1 >

In this example, a 4x4 matrix is multiplied by a 4x1 vector. The third element in the vector is set to 1 and all other elements are zero. The result of this operation is a vector which is made up of the third column of the matrix.

Example 2 >

In this example, a 4x4 matrix is multiplied by a 4x1 vector. In this case, two elements (2nd and 4th) in the vector are set to  1 and all other elements are zero. The result of this operation is a vector which is made up of the linear combination (sum) of the selected columns (2nd and 4th column) of the matrix.

Example 3 >

In this example, a 4x4 matrix is multiplied by the 2x4 matrix. You can think of the 2x4 matrix as a concatenation of the 2 selection vector (column selection vector). In this example, the 2nd element of the first column and 4th element of the second column in the 4x2 matrix are set to 1. In this case, two columns from the matrix are selected. The first selected column is the 2nd column of the matrix and the second selected column is the 4th column of the matrix.