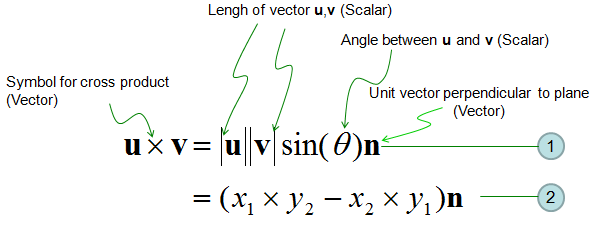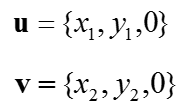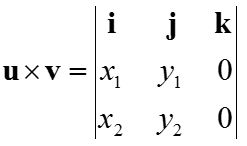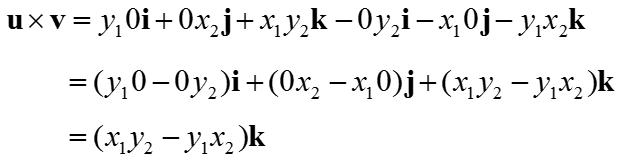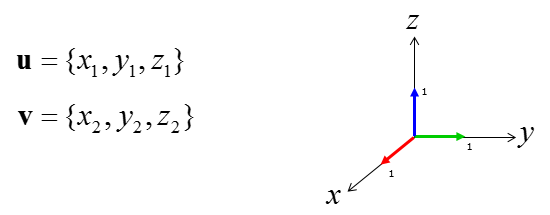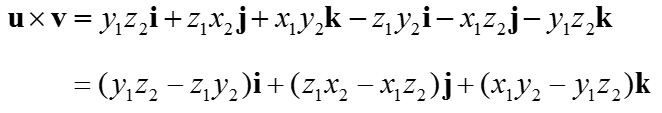Engineering Math - Matrix

Vector - Cross Product

It is pretty complicated process to calculate the cross product in terms of calculation process, but it is not that complicated to understand the geomatrical meaning for it. (Fortunately you don't have to calculate this by your hand. A lot of sotware package out there would do this for you. So what you have to do is just to understand the concept).

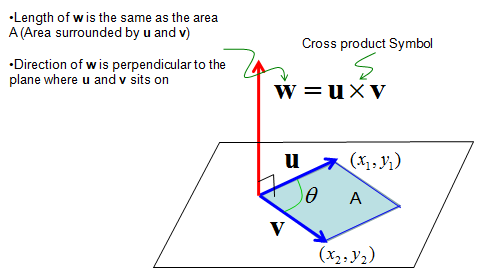
First thing you remember about the cross product is that the result of cross product of two vectors is also a vector (you would remember the result of inner product of two vectors is a scalar). By the definition of vector, it has both direction and size(magnitude).

Then, what is the direction of the resulting vector of cross product ?

It is normal (perpendicular) to the plane on which the two vectors sits on. It implies that if you get the cross product of two vector, you will get a vector which is normal to the two input vectors. This is one of the reason why 'cross product' is such a useful tool.

Then, what is the size(magnitude) of the resulting vector of cross product ?

It is the area of the area surrounde by the two vectors.

Following is the illustration showing what I described above.

Following is the concept of Cross Product represented in mathematical formula. The calculation shown in equation (2) may look pretty simple, but if the vector goes into higher dimesion the calculation goes exponentially complicated. But as I said, don't worry about this. Software would do it for you.

If you think of the meaning of the equation and illustration shown above, if both the vector u and v are on x-y plane, the resulting cross product vector is always in parallel with z axis.  

There is another way of calculating the cross product of the two vectors  u and v from a determinant equation as shown below.

Since the vector u and v is on x-y plan, you can represent these two vector as a three dimensional vector as shown below. (Why we need to make these vector as a three dimensional form ? It is because the cross product of the two vectors require at least three dimensional space.  It is because the resulting vector from cross product is perpendicular to the vectors given for the cross product. That is, the resulting vector of "u x v" is perpendicular to v and u. Even though you can represent u and v in 2 D plan, you need 3D space to represent u and v and 'cross product' all together.

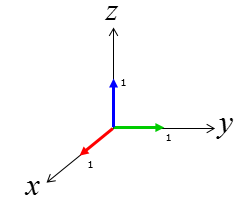
Now let's define three additional unit vector sitting along each of 3D axis as shown below.

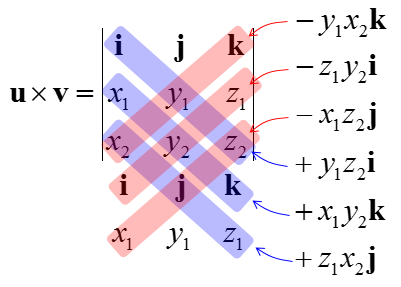
Once you have all the vectors described above, the cross product of the two vector u and v can be defined as a matrix determinant as shown below.

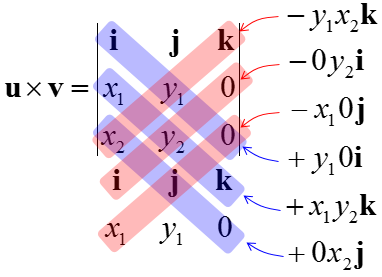
Now the remaining thing is just to calculate the determinant of 3x3 matrix. You can calculate the determinant of this matrix as shown below.

You may think that I am intentionally complicate a simple thing. At first look, it would look too complicated in terms of calculation but this one has an advantage.  If you want to calculate the cross product using the equation at the beginning of this page, you need to figure out angle between the two vectors. However, figuring out the angles between the two vectors is not easy (you would need to do Inner Product of the two vectors in order to figure out the angle between the two vectors). However, if you use calculate the cross product in this way (i.e, using the determinant), you don't have to worry about figuring out the angle between the two vectors.

Also using this way, you can get the cross product of two vectors in 3D space pointing two any direction (meaning the two vector u and v need not to be on x-y plane). You can represent any arbitrary two vector u, v and reference vector i, j, k as follows.

Using the same method shown above (described in more detail in Determinant page), you can calculate the cross product as shown below.