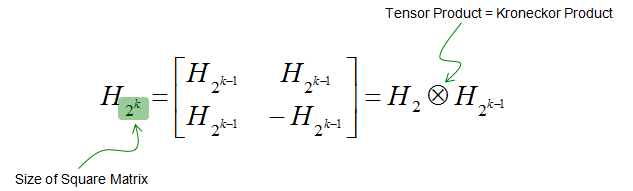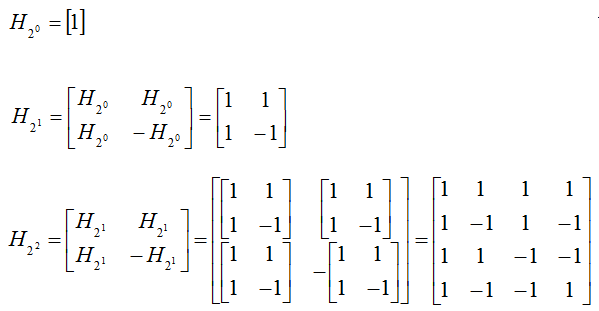|
Engineering Math - Matrix |
||
|
Hadamard Matrix
A Hadamard matrix is a special type of square matrix with elements either +1 or -1. The unique property of Hadamard matrices is that their rows and columns are orthogonal, which means that when any two distinct rows or columns are multiplied element-wise and then summed, the result is zero. In other words, the dot product of any two distinct rows or columns is zero.
How to generate bigger Hadamard matrix ?
We can generate a larger hadmard matrix from smaller hadmard matrix based on the following mathematical equation. This is basically recursive formula.
Example :
Application of Hadmard Matrix
Mostly thanks to the orthogonality property, Hadamard matrices are applied for some interesting characteristics and applications. For example, they are used in coding theory, signal processing, and experimental design. Additionally, Hadamard matrices are known to have the maximum determinant for matrices of their size, which means they are well-conditioned and have good numerical properties.
Coding theory: Hadamard matrices are used to construct error-correcting codes like the Hadamard code. These codes can detect and correct errors in data transmission, making them particularly useful in digital communication systems.
Signal processing: In communication systems, Hadamard matrices can be employed for spreading sequences in Code Division Multiple Access (CDMA) schemes. The orthogonal properties of the Hadamard matrix allow multiple users to share the same frequency band without interference. A typical example for this is Walsh Code being used in CDMA.
Cryptography: Hadamard matrices can be utilized in cryptographic schemes like the McEliece cryptosystem, which is a public-key cryptosystem based on error-correcting codes.
Compressed sensing: Hadamard matrices can be used to construct sensing matrices in compressed sensing, which is a signal processing technique for efficiently acquiring and reconstructing sparse signals.
Quantum computing: Hadamard matrices are used as the basis for the Hadamard gate, a single-qubit gate in quantum computing. The Hadamard gate is particularly important because it allows the creation of quantum superpositions, a fundamental concept in quantum computing.
Experimental design: In statistics, Hadamard matrices can be used to create orthogonal arrays for designing experiments. The orthogonality of the rows ensures that the experimental conditions are balanced, leading to more accurate and interpretable results.
Image processing: Hadamard matrices can be employed in techniques like the Hadamard Transform, which is a linear, orthogonal, and symmetric transformation used for image compression, data encryption, and pattern recognition.
Fast Fourier Transform (FFT) algorithms: The Fast Walsh-Hadamard Transform (FWHT) is a special case of the FFT that uses Hadamard matrices. It is a faster and more computationally efficient alternative to the regular FFT in certain applications
|
||