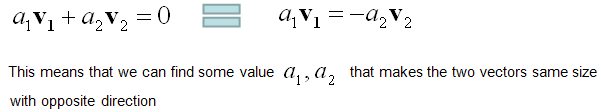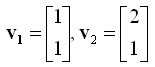|
Engineering Math |
||
|
Matrix- Linear Independence
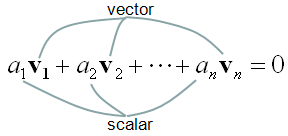
Linear Independence is an indicator of showing the relationship among two or more vectors. Putting it simple, "Linear Independence" imply "No correlation between/among the vectors". The mathematical definition of linear independence is as follows.
Like many other mathematical definitions, it is hard to grasp a clear understanding without going through examples. Let's suppose we have two vectors and want to check if the two vectors are 'linearly independent" or not. Applying the two vectors into the definition of linear independecy, we can express it as follows.
If I assume the two vectors are 2x1 vector, we can describe each component of the above mathemtical expressions as follows. As you see in this example, if we have only two vectors and the direction of vectors are different, they are 'linearly independent'.
If the two vectors are aligned in the same direction or in completely opposite direction (180 degree difference), we can easily find a non-zero a1,a2 value to make these two vectors 'NOT linear independent'.
Now let's see another example showing concrete numbers. Let's assume that we have two vectors as shown below.
Let's plug these two vector into the definition of linear independence. It becomes as follows.
If we plug the values into the expression, we get following expression.
Now the question is "Can we find any non-zero a1, a2 to satisfy this equation ?" and the result and the conclusion comes as follows.
Then the last question would be "Why the linear independency is important ?", "How do we utilise this concept ?". The importance of this concept would be for calculating the Rank of a matrix or for investigating the existence of solution of a simultaneous equation.
For more intuitive explanation, I want to introduce a good video linked here.
|
||