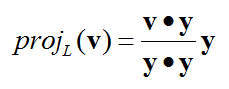Engineering Math

Vector - Projection onto Line

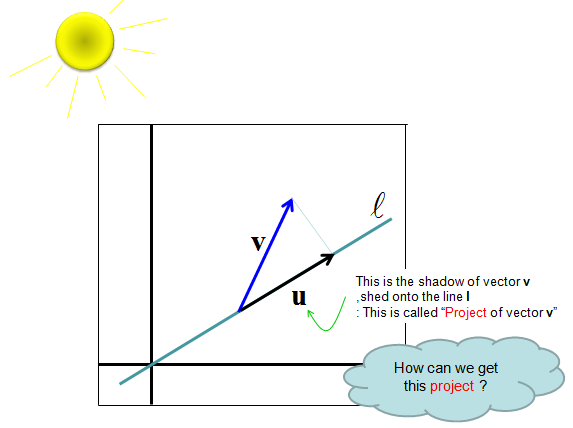
I will talk about "Projection" in this section. Here goes an intuitive situation describing the concept of projection.

Let's look at the following illustration. Here I have an vector labeled as v (Blue arrow) and the starting point of it is attached to a line labeled as l. Now we have a sun (light) shining right above the vector. Then you would have a shadow of the vector v on the line. The shadow would like like the vector labeled as u(Black arrow). This shadow vector is called a 'Projection' of the vector v.

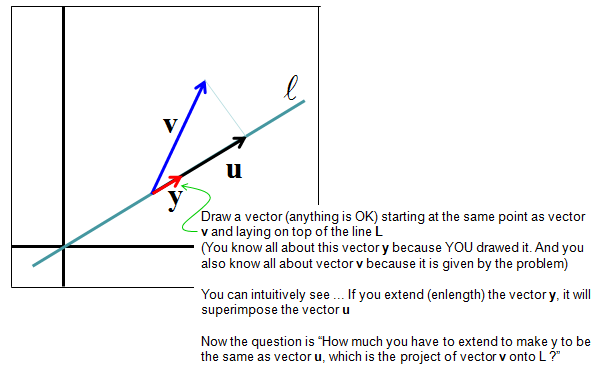
Now let's think about how we get this shadow vector (projection) mathematically. The method is as described below.

The conclusion (final equation) is as follows.

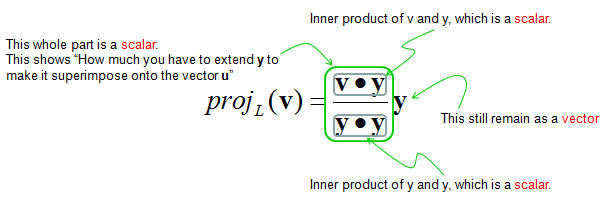
I would not prove this equation itself. You can refer to Linear Algebra text book if you are interested in how this equation are drawn. But it would be worth understanding each component of this equation as show below.

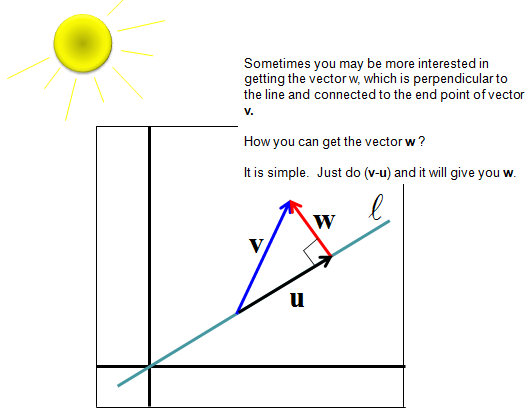
Then... Let's think about why we need this kind of operation. You can utilize this one to get the shadow of an object on computer graphics.. and more common application in a variety of application it is used to get a vector which connecting a point to a line in the shortest path. Just taking the magnitue of vector w in the following illustration gives you the distance (shortest path) between a point and a line.

Summary

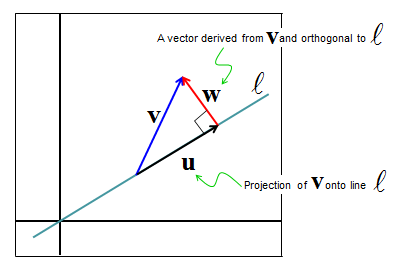
From derivation of Projection vector onto a line as explained above, we can figure out two important vectors as illustrated below. Both of these two vectors are widely applied in many cases. The vector u would be widely used in geometric transformation and the vector w is used in matrix orthogonalization and linear regression.