SVD (Singular Value Decomposition) - Application - Image Compression

In this application, I assign the whole pixel data of an black-and-white image to the matrix M

M = imgBW; % 511 x 513 image, 511 x 513 data

Then I did SVD as follows.

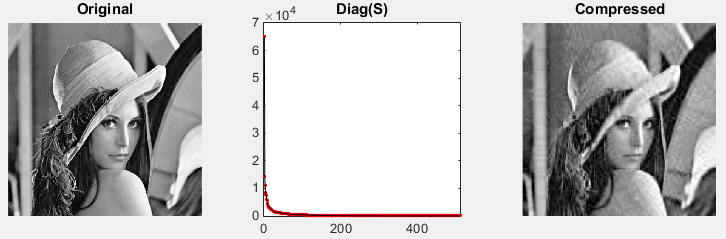
Then take out only n colums from U and V matrix and take out (n x n) submatrix from S as shown below.

Uc = U(:,1:n);

Sc = S(1:n,1:n);

Vc = V(:,1:n);

Then reconstruct the image from these submatrix as follows.

CompressedImage = Uc * Sc * Vc   (Note : '*' indicate the matrix multiplication(Inner Product))

Following result shows you the Original Image and all the diagonal values of S matrix and CompressedImage. This is the case when n = 30; In this case, Uc is (511 x 30) matrix, Sc is (30 x 30) matrix, Vc is (513 x 30) matrix.

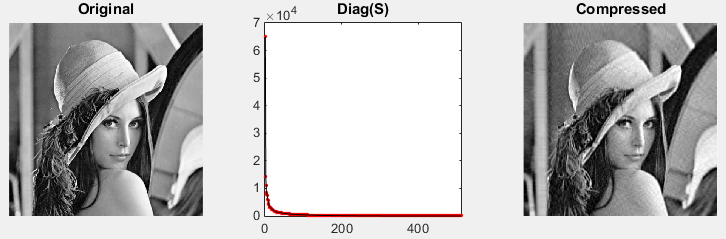
Following result shows you the Original Image and all the diagonal values of S matrix and CompressedImage. This is the case when n = 50; In this case, Uc is (511 x 50) matrix, Sc is (50 x 50) matrix, Vc is (513 x 50) matrix.

< List 1 >

clear all;

 

img=imread('Lena.png');

imgBW = rgb2gray(img);

 

M = imgBW;

 

[U,S,V]=svd(double(M));

Sd = diag(S);

 

n = 30;

Uc = U(:,1:n);

Sc = S(1:n,1:n);

Vc = V(:,1:n);

CompressedImag = Uc*Sc*Vc';

 

subplot(1,3,1);

imshow(M);

title('Original');

 

subplot(1,3,2);

plot(Sd,'ro','MarkerFaceColor',[1 0 0],'MarkerSize',2);

hold on;

plot(Sd,'k-');

hold on;

xlim([0 length(Sd)]);

title('Diag(S)');

 

subplot(1,3,3);

imshow(uint8(CompressedImag));

title('Compressed');