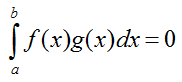|
Engineering Math |
||
|
Orthogonal/Orthogonality
Orthogonality can be represented in many different ways depending on the situation where they are used.
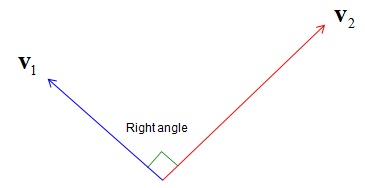
When we talk about Orthogonality in vectors represented in a graph (in a coordinate system), the orthogonal means the angle between any two vectors are 90 degree (right angle). It doesn't matter of magnitude of the vectors.
This kind of graphical representation would be easy to understand or intuitive, but you cannot represent orthgonality in this way if the dimension of a vector is larger than 3.
Another way of expressing the orthogonality of the two vectors is to use the inner product. When the inner product of two vectors is zero, we say the two vectors are orthognal to each other. In this way, we can check the orthogonality of two vectors with any dimension (size). This is the most commonly used concept of Orthogonality in engineering.
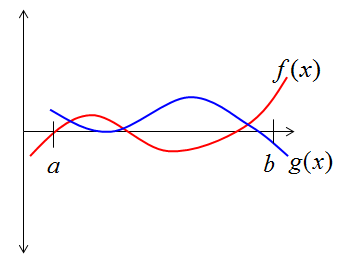
We can define orthogonality not only for two vectors but also for any two functions. Let's suppose we have two function f(x) and g(x) as follows.
If you multiply two functions and integrate over a certain span and the result is zero, we say the two functions are orthogonal over that span. For example, if we have two function that satisfy the following relation, we say f(x) and g(x) are orthogonal between 'a' and 'b'.
What is the practical meaning of the orthogonality ? This is the most important in engineering application. If two vectors are orthogonal, it means there is zero correlation (no correlation at all) between the two vectors (or two data sets).
|
||