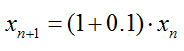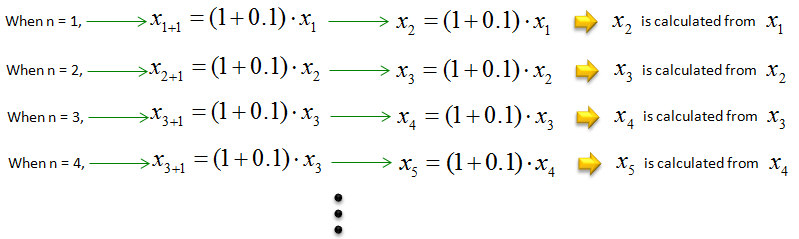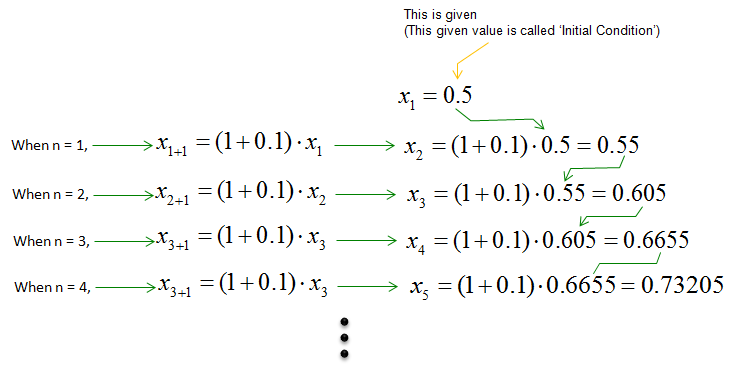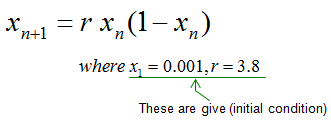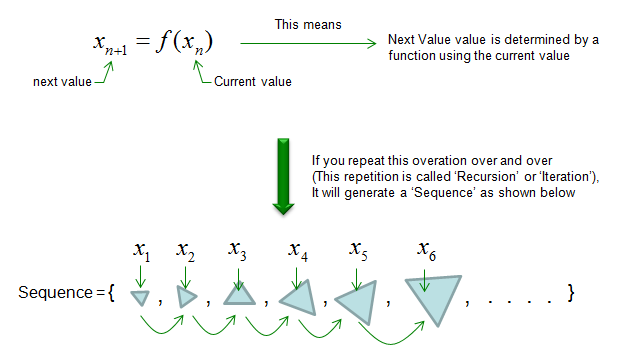
Recursion or Iteration means "doing the same process over and over".  If you represent this expression in mathematical form, it can be expressed as shown below. I hope this make sense to you.

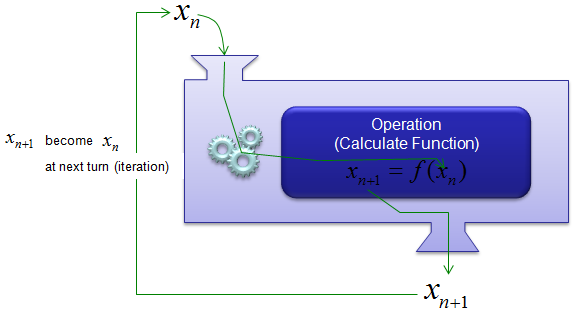
If you illustrate the iterative/recursive process in more intuitive form, you can illustrate it as follows. If we take a function (f(x)) as a machine to generate a product(output) from a raw material (input). In this machine, if you put anything (input = raw material), you would get a product (output). And then you take the output and put it as the input of the machine, you would get another output. And then you take that output and put it as an input. you would get another output. This kind of repeating process is called 'iterative or recursive' process.

Why we care about this kind of process ?

One of the main reason is that the output of even a very simple iterative function generate very complex-looking output. In many cases, when we meet a very complicated things (phenomena), we tend to day "This is too complicated to explain in a certain scientific rule" and give up trying to find rule itself. For example, what would you say if somebody ask you "Look at all the branches of that big tree. Would that be any rules how each of those branches are formed ?. In other words, can you draw anything like those tree using some mathematical procedure ?". or what would you say if you are asked "Look at the spiky rocks, can you draw any similar shap like that using a mathematical procedure ?".

Even until very recently (before we pay attention to 'iterative/recursive' functions), the questions to these questions were ".. It is just natural phenomena.. there is no specific rules .. or the rule is so complicated that we cannot explain in curent scientific method. But now a lot of those complicated phonomina can be explained by sprisingly simple iterative function or iterative process. and the iterative function/process is the foundation of Fractal and Chaos.

Example 1 >

This example illustrates a recursive mathematical relationship where each term in a sequence is calculated based on the previous term using the formula. The important point is that each term depends directly on the previous term in the sequence, which is emphasized in the step-by-step process shown in the diagram. This recursive process ensures that every new term builds upon its predecessor.

Starting with x₁ (the initial term of the sequence):

•   x₂ = (1 + 0.1) x₁
•   x₃ = (1 + 0.1) x₂
•   x₄ = (1 + 0.1) x₃
•   x₅ = (1 + 0.1) x₄

This pattern continues iteratively, with x_n+1 being derived from multiplying x_n by (1 + 0.1) for every subsequent n.

As you see here, if you know the initial condition (x₁) you can figure out all of the subsequent numbers (x₁,x₂,x₃,x₄ etc) . How can I figure out the initial condition ?

NOTE : In most of the text book, starting point (the initial condition) is represented as x₀ but I represented it as x₁ because '1' looks more like a 'starting point' than 0. It doesn't matter.. you know the point

How can I figure out the initial condition ?  Simple. I should be given or you just pick any number on your own. You may pick just any arbitrary number just for practice, or you may need to pick the number carefully if this model is associated with a specific real life problem.

Just for practice, let's assume that the initial number x₁ is 0.5. Then you can plug this number and calculate the subsequent numbers as follows.

Example 2 >

This example shows a practical example called 'logistic map equation'. It is one of the most frequently used example when we talk about recursive function.

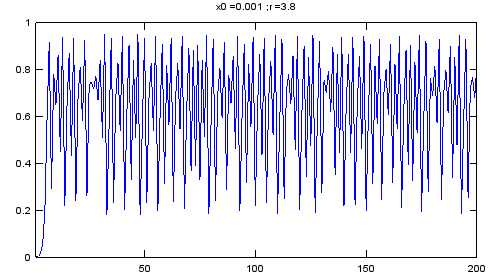
This model is widely used to study population dynamics, where x_n might represent the population at time n, r represents the growth rate, and (1 − x_n) accounts for limited resources or competition. In this context, the chaotic fluctuations could model unpredictable population changes under certain conditions.

Following is the plotting of x_n recursively calculated by the method explained in example 1

Behavior Shown in the Plot:

The graph displays the values of x_n over successive iterations, starting with x₁ = 0.001 and r = 3.8.

The horizontal axis represents the iteration count (n), while the vertical axis represents x_n, the value of the sequence at each step.

Observations from the Plot:

• Chaotic Behavior:
• The sequence does not settle into a fixed point or periodic behavior but instead fluctuates irregularly.
• This behavior is characteristic of chaotic systems when the parameter r is in a certain range (e.g., r = 3.8 in this case).
• Sensitivity to Initial Conditions:
• The chaotic behavior of the system implies that small changes in the initial conditions (x₁) or the parameter r can lead to dramatically different sequences.
• Logistic Map in Chaos Theory:
• At r = 3.8, the system demonstrates one of the key properties of chaotic systems: seemingly random behavior emerging from a deterministic process.