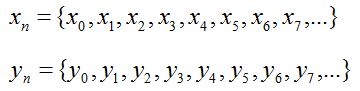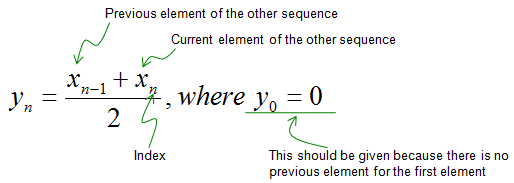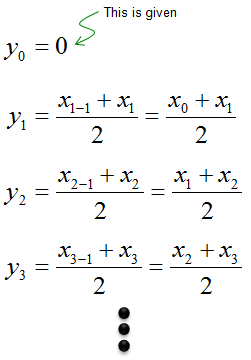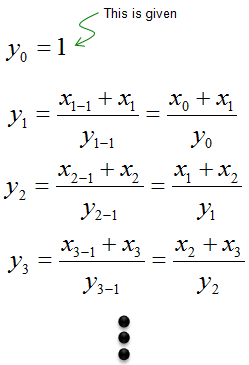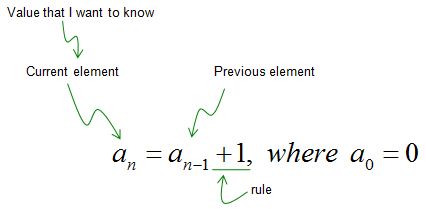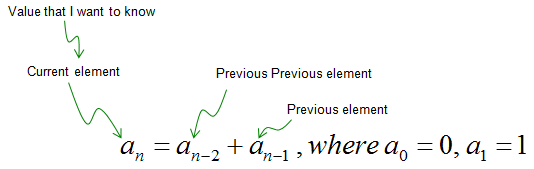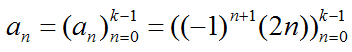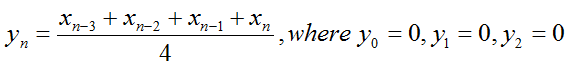|
Engineering Math |
||
|
Sequence
Sequence is a bunch of any entities (objects) arranged in a specific order. Any elements (entities) can create a sequence. It can be numbers, alphabets, even formulas.. but one condition is that there should be a certain rules between an elements and previous elements). Simply put we should be able to find a certain rules to create a given sequence.
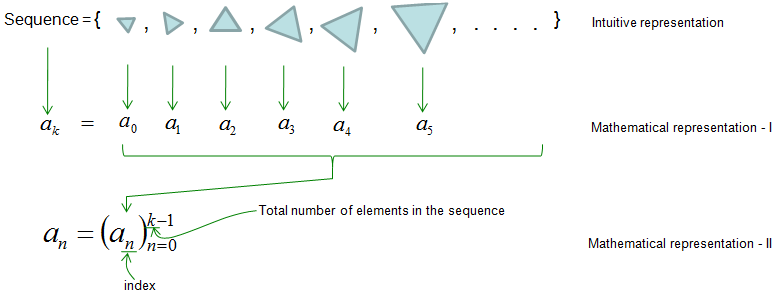
If I represents a sequence in an illustration, it can be as shown below. This illustration shows many triangles arranged in a certain pattern. So we can call it as "a sequence of triangles in pattern X" (Let's think about the 'pattern X' later).
Important things about the sequnce in practice is to understand and get familiar with mathematical representation of the sequence. There are several different ways of mathematical representation of the sequence. It is important for you to get familiar with all the different types of representation.
One of the most common way of representing a sequence in a mathematical form is the one as labeled 'Mathematical representation - I'. It assigned a letter 'a' as indicating elements of the sequence and uses subcriptions (I call this as an 'index') to indicator the specific position of the element 'a' within the sequence. Notice that the index starts from '0', not '1'. Starting from index 0 is not a mandatory. you can label it from index 1 if you like, but it is more common to use index 0 as the starting element. Another form of mathematical representation would be as labeled as 'Mathematical representation - II'. It is much more compact than the 'Mathematical representation - I', but it may look more intimidating (scary) if you are not familiar with this area.
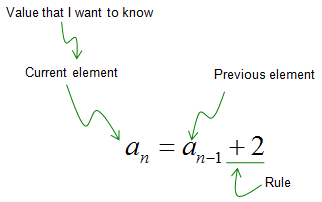
The two forms mathematical representation shown above would show the 'order' of the elements within the sequence, but it does not show the relationships between an element and another element. To show this relation between elements sometimes we represents a sequence as follows. This examples shows 'within the sequence 'a', an elements can be generated from the previous element and a 'rule'.
What do you see in terms of pattern in the triangle sequence you saw at the beginning ? Are they arrange in a random pattern ? Let me give you the answer since I am the one who created the sequence -:) a(0) = first triangle = this should be given by the person who created/defined the sequence since there is no previous element. We cannot apply any 'rule' to create the first triangle in the example. a(1) = second triangle = expand the first triangle a little bit and rotate it to the right a little bit. a(2) = third triangle = expand the second triangle a little bit and rotate it to the right a little bit. a(3) = fourth triangle = expand the third triangle a little bit and rotate it to the right a little bit. a(4) = fifth triangle = expand the fourth triangle a little bit and rotate it to the right a little bit. Now can you see any pattern and describe the triangle sequence in a mathematical form ? I can be represented as follows.
a(n) = 'expand and rotate a(n-1)', where n > 0
It means that any element (except the first element) can be created by 'expanding and rotating a previous element.
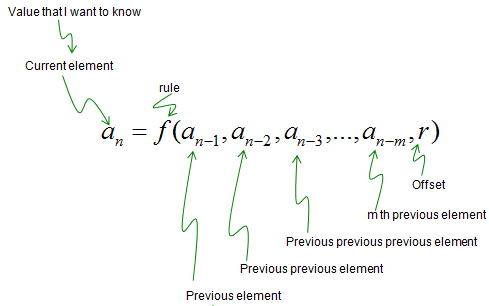
In this example, we saw a case where an element is created by apply a rule to only 'IMMEDIATE PREVIOUS' element, but this is not the only case. There can be some case as follows
If we represent this kind of sequence generation in a more formal form (fancy but scary -:)), it would look as follows. f() in the form represents a rule. Just don't get scared.. just don't run away and take closer look at the mathematical form and describe it in plain language as I did above.
I just described a couple of most common form of mathematical representation for a sequence. There would be other variations. Whenever you see a sequence in a mathmatical form, try to create several elements of the sequence on your own until you get the clear understanding of the mathematical representation.
Please refer to the following link (if you want to get some high school class style explanation) : Math is Fun - Sequence (I think this is excellent explanation)
The sequence I metioned above is something that you might see often in your math class. In case of engineering course, you may more often see the sequence as follows. All most all the engineering area dealing with discrete data (e.g, digital data) would use this kind of sequence. So you'd better be very familiar with logic behind these and mathematical representation introduced here.
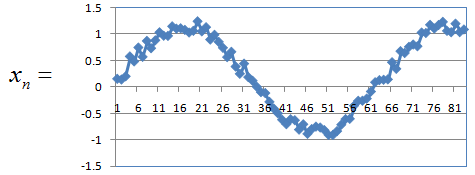
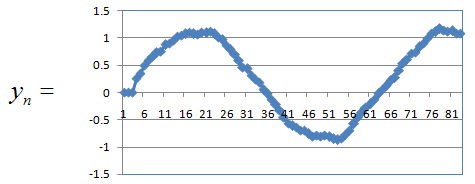
In this case, a sequence (labeled as y(n) is created from another sequence (labeled as x(n)) by applying a certain rule.
Let's assume we are given a sequence generation rule as shown below
You can generate each elements of the current sequence (y(n)) just by plugging in elements of the other sequence (x(n)) according to the rule as shown below.
Now let's look into another example sequence which is generated from combination of the other sequence (x(n)) and the current sequence (y(n)).
Let's assume that we are given the sequence generation rule as shown below. Notice that the rule here contains not only 'the other sequence (x(n))' but also the current sequence (y(n)).
Just plugging in appropriate elements of the sequence x and y, you can generate each of the elements of sequence y as shown below.
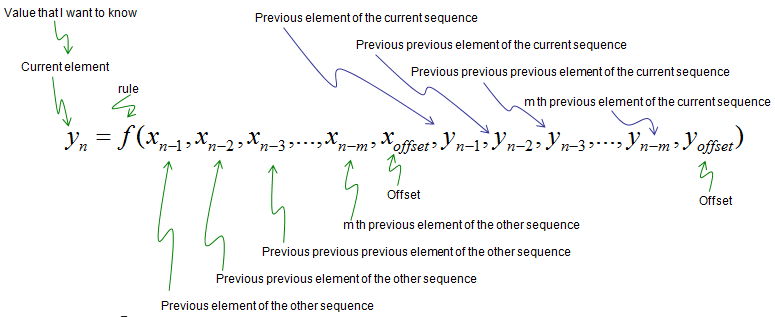
You can represent a general rule to create a sequence y based on both the sequence x and sequence y as shown below. Just don't get panic and skip this part. Just try to think of each component of the expression and describe it in plain language.
Now let's look into several examples to get you more familiar with the concept or mathematical representation of a sequence.
Example 1 >
Find the mathematical rule for the following sequence.
I know you intuitively grasp the meaning of this sequence.. but may have some difficulties in representing in a mathematical form. If you look into the sequence more closely, you would notice that the value of each element is same as the index of the element. So this sequence can be represented as shown below.
How do you know if this is correct mathematical representation of the sequence ? It is simple. Just try to create each elements of the sequence from this rule.
Can you find another rule showing the relationship between an element (or multiple elements) and another element ? It will come out as follows. Can you make sense out of this equation ? It says "An element of the sequence can created by taking a 'previous element + 1'.
Example 2 >
Find the mathematical rule for the following sequence.
I know you intuitively grasp the meaning of this sequence.. but may have some difficulties in representing in a mathematical form. If you look into the sequence more closely, you would notice that the value of each element is same as the index of the element. So this sequence can be represented as shown below.
How do you know if this is correct mathematical representation of the sequence ? It is simple. Just try to create each elements of the sequence from this rule.
Can you find another rule showing the relationship between an element (or multiple elements) and another element ? It will come out as follows. Can you make sense out of this equation ? It says "An element of the sequence can created by taking a 'previous element + 2'.
Example 3 >
Find the mathematical rule for the following sequence.
Unlike previous two examples, I don't think you come out with any pattern in such an easy way. Can you find any answer to the following questions ?
Don't get disappointed if you failed to find a rule for this. I am pretty sure that I would not find the rule if I haven't r recalled a special pattern called 'Fibonacci sequence' that I learned in high school math. Definately this is not what I found, it is just what Fibonacci found.
Anyway the answer is as follows. It says an elements in the sequence can be created by taking "previous-previous element + previous element'. Since it requires two previous elements, the first two elements should be given as shown below. Depending on which value is given to the first two elements, the value for all the next elements will get different.
Example 4 >
Now let's look into another example. Now I will give you just a rule for creating a sequence. Even though it would be a little daunting (scary) since it is a mathematical form, it would be much easier to generate the sequence if the rule is given.
As you are already familiar, 'n' in this rule indicate 'index' (location of the element in the sequence). This rule says "If you only know the index of an element, you can generate the value for the element just by plugging the index into the rule as shown below.
With these calculated values, you can come out with a sequence as shown below. Isn't it simple ?
Example 5 >
Let's assume we have the following sequence.
Assume that the sequence y is created by another sequence x according to following rule.
Assume that the sequence x has elements as shown below.
The sequence generated by the given rule should be as shown below. (For the generation of each elements of the sequence y, look into this spreadsheet)
|
||