Engineering Math

Series : Taylor Series/Taylor Expansion/Maclaurin Series

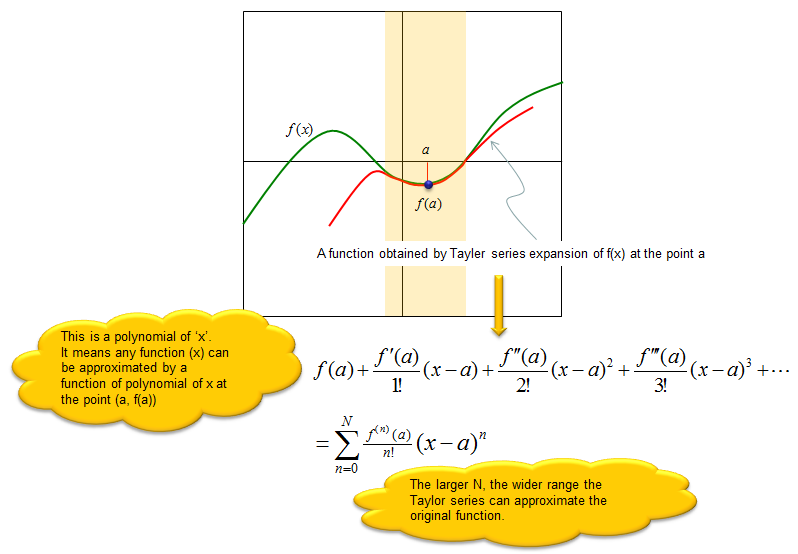
Tayler Series is a kind of technique to approximate any form of function around a specific point in the form of polynimial function. Let's look at the following illustration as an example. Let's suppose that we are given a function called f(x) that is plot in green curve. Now look at the graph plotted in red. As you see, the red plot has exactly same value as f(x) at the point 'a' and within a certain range (marked as orange background) the red graph is almost same as the green graph (f(x)). In this case, we can say the red plot is a approximation of green plot (f(x)) around the point 'a'.

Then you may ask 'how can we get (derive) the equation for the red graph ?'. One of th enswer to this question is Taylor Series as described below.

Now you would ask 'Why we need or use this kind of series expression ?'. Before I answer to this question, let me ask a question to you first. When do we use 'approximation' ? Approximation is just 'similar value' but not exact/accurate value. So it cannot be as good as the exact value. Then why do we still use approximation sometimes ?

It is because it is easy to use or easy to calculate even though we need to sacrifice a certain degree of accuracy.

This logic applies to Taylor Series as well. Taylor series is a approximation to a given function which may have similarity to the original function only within a certain range. But we still use this series because it is easy to use and simple to calculate in many case.

You may think 'look at the series equation.. it doesn't look simple.. it has a lot of derivatives (it may scare you) and equations gets very long.

Many people tend to think 'An equation is very complicated or hard if it is very long', but it is not true. 'Length of a equation' and level of difficulty is completely different story. Even though the Taylor expanded equation tend to be long, all the derivative terms (f'(a), f''(a), f'''(a)) will become a constant if you plug in a specific 'a' value. So the expanded equation (the series) become a polynomial of the variable 'x'. The polynomial function is one of the most common function everybody learned in high school math. However long it is, we don't feel much difficulties understanding/solving the equation.

So the main usage of Taylor series is to approximate a function with a simple polynomial function which is well known to everybody.

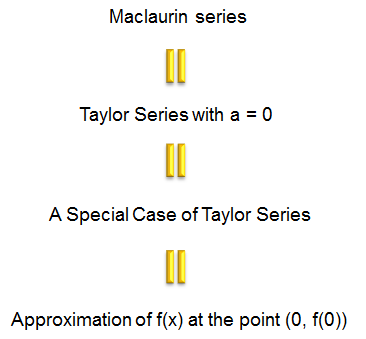
Similar to Taylor series, there is another special series called Maclaurin Series. Actually Maclaurin Series is just a special form of Taylor Series. Taylor Series is an approximation of a function at any point 'a', but Maclaurin Sieries is an approximation at the point '0'. It means if you replace 'a' in Taylor serious with '0', you will get Maclaurin Series equation.

Example 1 : Taylor and Maclaurin Series of Exponential Function

In this example, we are given an exponential function. Can we approximate this function in the form of polynomial ?

Yes, we can get the approximation using Taylor series expansion as follows. And if you plug '0' into 'a' in the derived Taylor series equation, you will get the Maclaurin series for the exponential function.