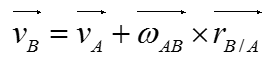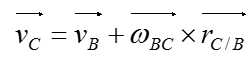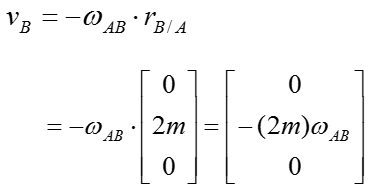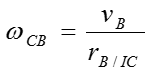Mechanical Engineering

  

 

 

 

Linkage System : Relative Motion Analysis : Velocity

 

All of linkage system problems involve relative-motion analysis because the motion of a link is affected directly by the motion of its adjacent link

Must be comfortable with setting up vectors as well as executing vector addition, subtraction, and multiplication by hand

Scalar method/approach can also be used as an alternative method for the vector method and is favored over the vector method as it is less time consuming

 

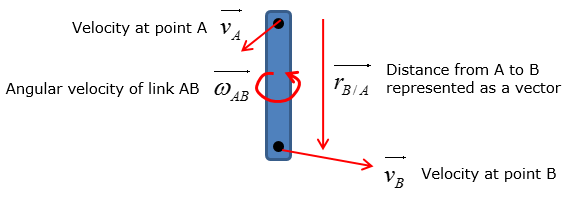
Let's consider a simple linkage system as shown below

 

 

Velocity of the link at point B is calculated by using the following equation if vector method is to be used

 

 

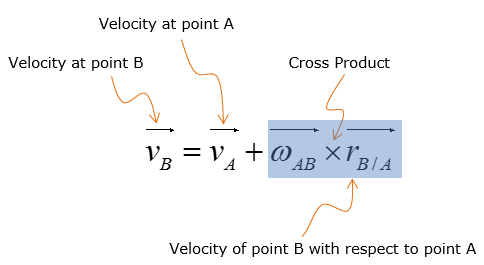
Putting a short description on this equation as follows would help you with understanding this equation. The equation states that the velocity at point B of the rotating link AB is dependent on the sum of the velocity at point A and velocity of point B with respect to point A

 

 

 

Example 1 >

 

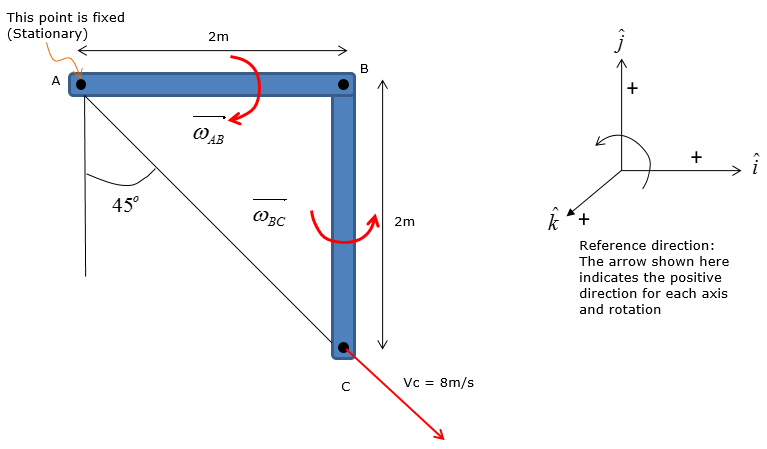
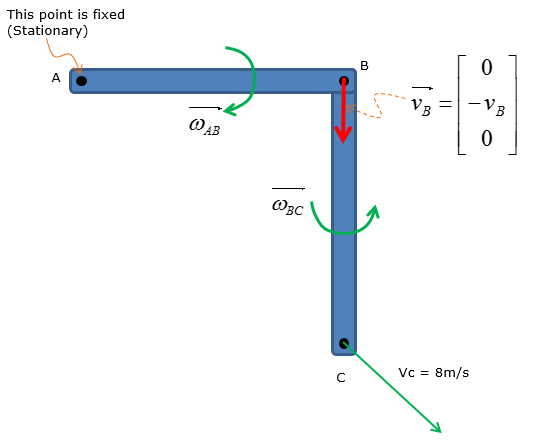
The slider block C moves at 8 m/s down the inclined groove. Determine the angular velocities of links AB and BC, at the instant shown.

 

 

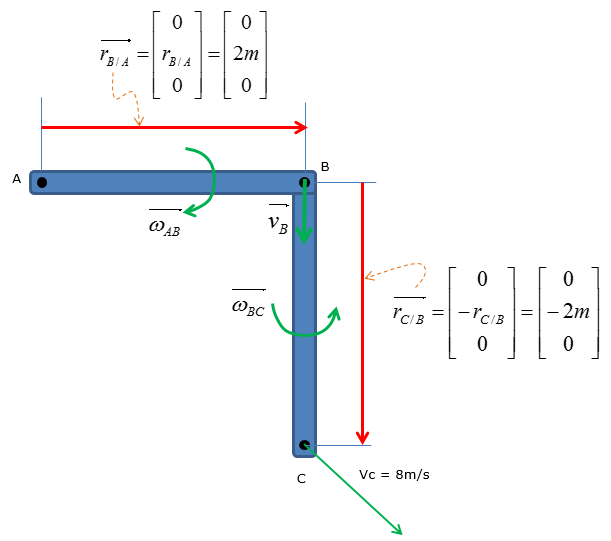
Step 1 >  Situational analysis – set up the vectors

  • For any linkage velocity problems, you must know the direction of the velocity vectors at each pivot points, which are points A,B, and C this case
  • In this case, the velocity at point A is 0 because it is stationary
  • To allow point C to move in such direction, link BC must rotate counter-clockwise and link AB must rotate clockwise
  • Since link AB rotates in a clockwise direction about point A, the velocity vector at point B points downward can be represented as follows :

 

  • Compute the distance vectors for link AB and link BC:

 

 

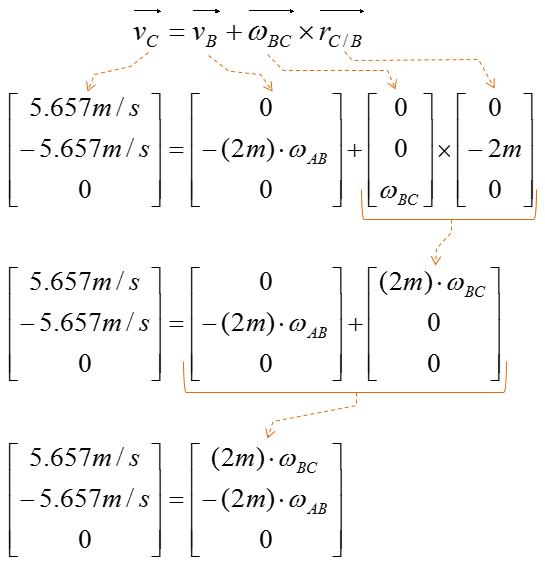
Step 2 >  Plug in the vectors into the relative velocity equations to obtain simplified expressions  

  • To calculate the angular velocity of link BC, first plug in all the vectors for the expression for velocity at point C

  • Since point B rotates about point A in a clockwise direction, the velocity of point B can be expressed as following

  • Plugging this into the first equation, you would get

 

 

Example 2 >  Scalar method of relative velocity analysis  

 

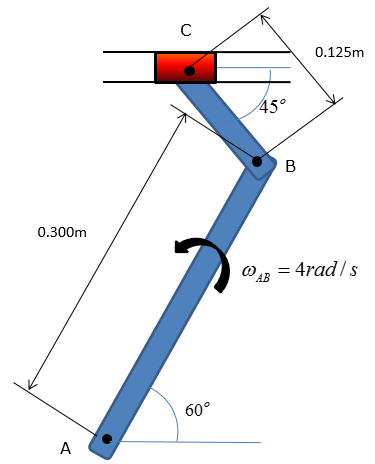
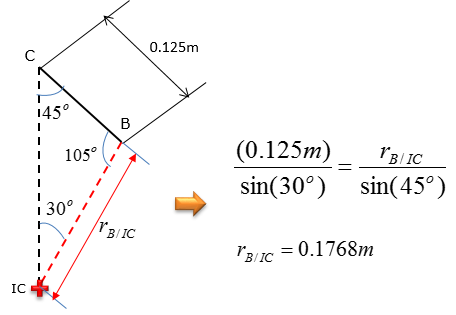
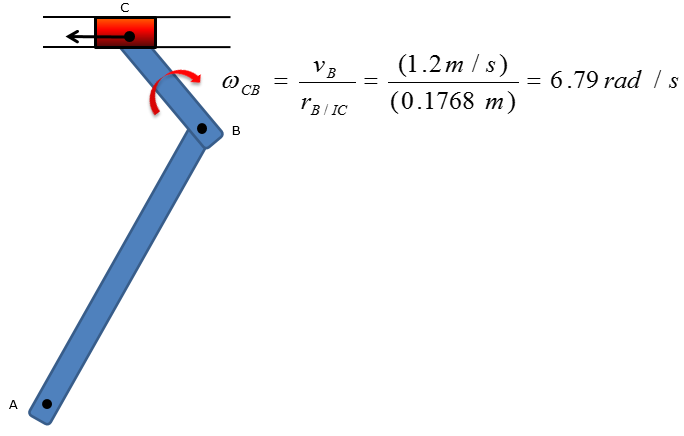
Scalar method of relative velocity analysisThe shaper mechanism is designed to give a slow cutting stroke and a quick return to a blade attached to the slider at C. Determine the angular velocity of the link CB at the instant shown, if the link AB is rotating at 4 rad/s

 

 

 

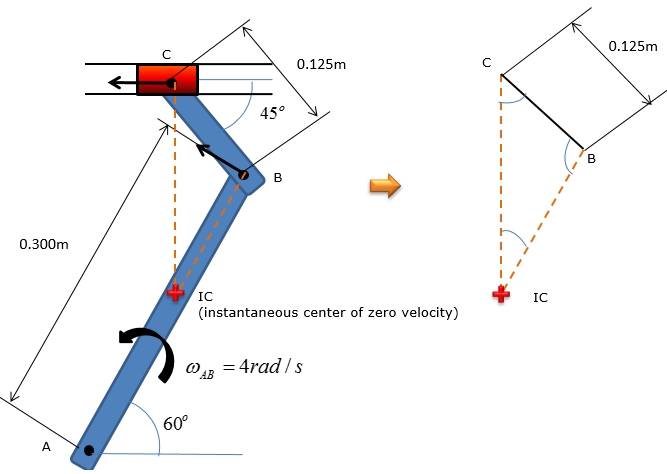
Step 1 > locate the instantaneous center of zero velocity  

  • Start the question by drawing the velocity diagram of the linkage system
  • Draw an orthogonal line for all the velocity vectors and locate the point of intersection for the lines
  • The point of intersection is the instantaneous center(IC) of zero velocity

 

 

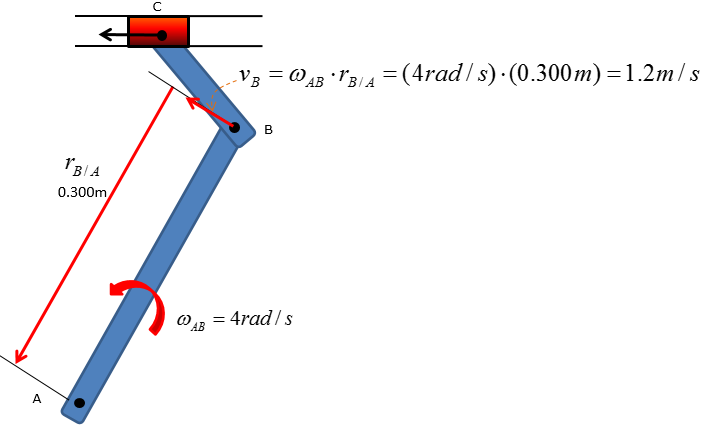
Step 2 > Calculate the angular velocity of link CB

  • Since point A is the stationary pivot point of link AB, velocity at point B can be calculated by using the length of link AB and the given angular velocity of the link:

  • As velocity at point B is known, it can be used to calculate the angular velocity of link CB. And the angular velocity is calculated as following

  • In the equation above, the magnitude of   needs to be computed before calculating the angular velocity. The magnitude will be calculated through trigonometric analysis of the simplified instantaneous velocity diagram shown below.

  • Plug in the distance between point B and IC into the angular velocity equation for link CB