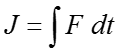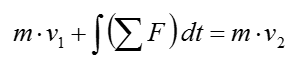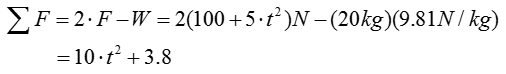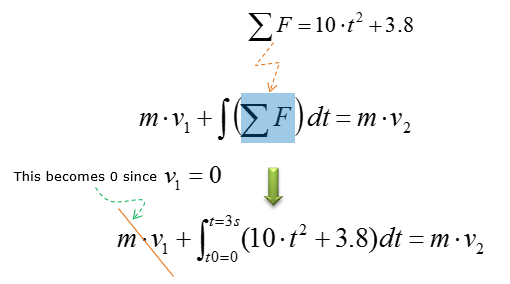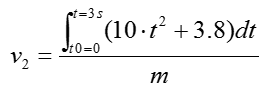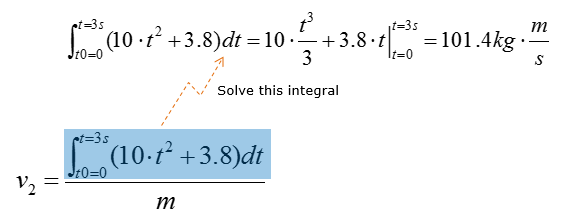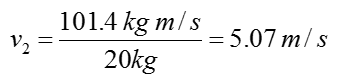Mechanical Engineering

  

 

 

 

Impulse and Momentum

 

Principle of impulse and momentum is used to analyze the motion of an object in motion based on time-change due to applied force(s).

 

First let's think of what is Momentum and what is impulse. You may find various types of definitions from internet or textbooks.  My definition would not be much different from what you would have seen in internet or in textbook. I would define these terms as follows.  

 

Momentum : It is a physical quantity that indicates the status of an object in motion. It indicates how fast an object is moving at a certain time. Probably the mathematical definition would sound clearer because the equation is very simple as follows.

 

 

Impulse : It is a physical quantity that indicates how much forces are applied to an object for how long. Mathematically it is defined as follows.

 

 

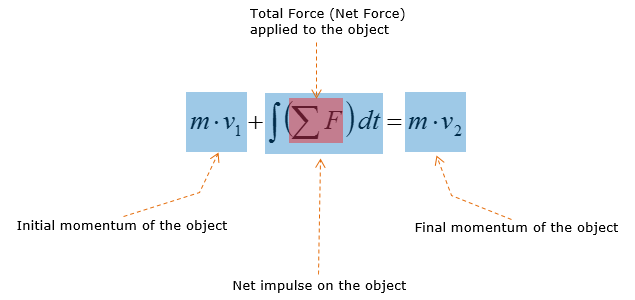
Actually more important than understanding the definition of each terms is to understand how these two physical quantities are inter-related in real situation. These two quantigies are inter-related in the governing equation as shown below.

 

 

 

What does this mean ? Does it make sense to you ?

 

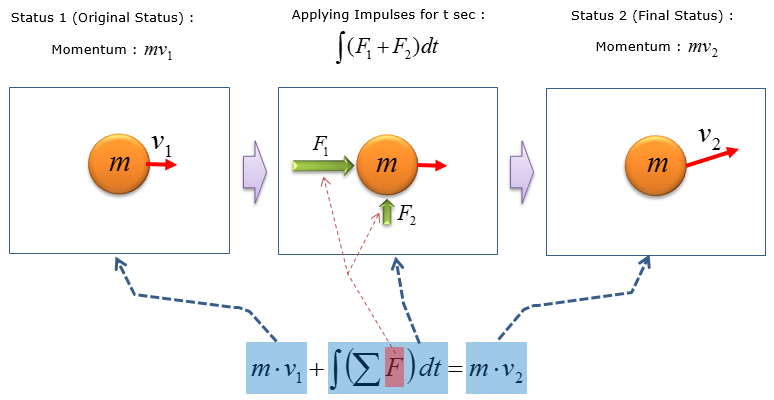
Let me explain this equation with an illustration as follows. I hope this would give you more intuitive understanding.

 

 

 

As you see in this equation, you don't need to know of the magnitude of acceleration to calculate the initial or final velocity of an object and this is why this form of equation is more widely used over other kinematic equations

 

 

What can we apply this for ? / Why we need to know about this ?

 

There are many fields you can apply this technique for, but followings are a couple of typical application of this technique.

 

Construction site:

  • Calculating the force required for a crane to generate in order to lift up building materials, such as pipes, steel rods, etc
  • Calculating for the velocity of a jack hammer after it rebounds from the ground based on the applied impulse to the ground

 

Driving:

  • Calculating the impulse on the car after it crashes
  • Estimating the speed of the car after certain period of time

 

 

Example 1 >

 

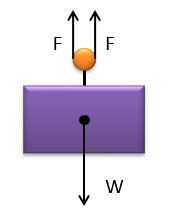
The 20 kg crate is lifted by a force of F = (100 + 5 t^2) N, where t is in seconds. Determine the speed of the crate when t = 3s, starting from rest

 

 

Solution >

 

Since F is a function of time, principle of impulse and momentum is used as the governing equation for analyzing the final speed of the crate.

 

Step 1 : Compute the equation for the sum of the forces acting on the crate to calculate the speed of crate after 3 seconds.

 

 

Step 2 : Now let's plug this result into the governing equation that we described at the beginning of the page.

 

 

 

Step 3 : Now simplify a little bit and rearrange the equation with reference to v2 (because this is the one we need to figure out). Then we get the equation as follows.

 

 

Then, let's solve the integral part first to simplify the equation further

 

 

Plugging into all the values into the equation, we get the final result as follows