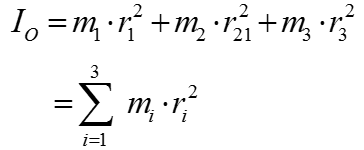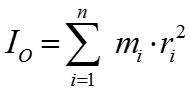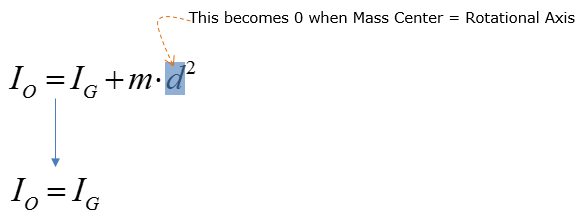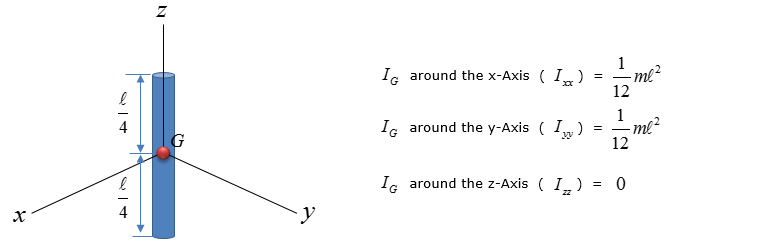Mechanical Engineering

Mass Moment of Inertia

Mass moment of inertia is a quantifiable property that determines the ability of a rigid body system to resist the change of the rotational speed about its pivot point. The shape and mass of a solid determines the magnitude of mass moment of inertia about the mass center of an object. However, for most 3D figures, the magnitude of mass moment is also affected by the direction of the rotational axis of the rigid body. Mass moment of inertia about the mass center can be applied for rigid body rotation about both fixed and translating axis.

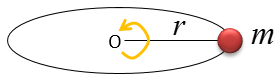
To understand how the Moment of Inertia is described in a quantitative form, let's think of one of the simplest case as shown below. A mass connected to a string is rotating around a fixed point (O).

The Moment of Inertia for this system can be described mathematically as follows. You can notice that the moment of Innertia is proportional to the mass m and the sqqure of distance between the rotational axis and the mass.

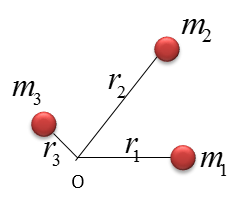
Now let's extend the simplest case into a little bit complicated form as follows. In this case, three different masses are rotating around the same axis of rotation.

Assuming that all of the masses are rotating in the same direction, the moment of inertia of this whole system can be described as follows.

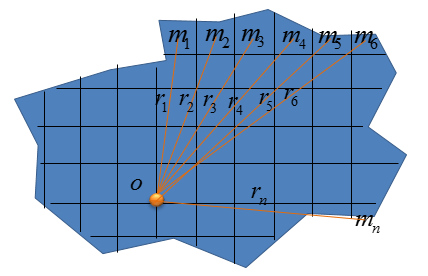
If you extend the two cases shown above to an extreme case, you can estimate the moment of the innertia of any arbitrary form by splitting the whole object into many, many small segments that are all tied to the origin of axis (O) as shown below.

As you may easily guess, the moment of inertia of this shape can be described as shown below. If you apply mathematical tricks, you may extend this to integral form (I will leave this up to you for now)

Moment of Innertia for a Rectangular plane

Even though you can calculate (estimate) the moment of Inertia as you did for Arbitrary shape described above. It is not always easy to do in your daily engineering work. If the shape of an object is pretty simple like rectangle, disk with the same material density all over the object, there would be much simpler way to calculate the moment of inertia whiout using the complicated Integral form (summation form).  

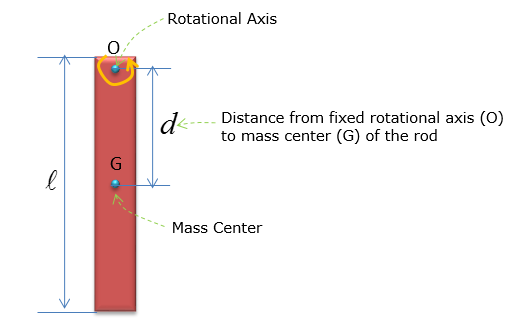
Let's assume an object in a rectangular shape as shown below. For fixed axis rigid body rotation, mass moment of inertia about the fixed axis is always preferred over the mass moment about the mass center, as one does not have to consider the linear velocity of the object at the mass center (indicated as G).

The moment of inertia when the object is spinning around the point O can be expressed as follows.

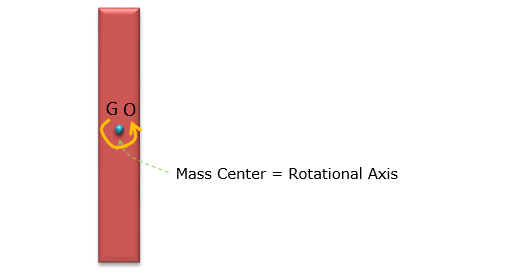
Now let's think about the case where the center of the mass and the center (axis) of rotation is same. It means that the object rotates around the mass center.

Then the equation for the moment of innertia can be simplied as shown below.

Moment of Inertia for Various Shapes

As briefly mentioned above, the most critical factors to determine the moment of the innertia is the shape of the object and the axis of the rotation (the density of the material at each point in the object plays important role as well, but we can ignore the density part if we assume that the density is same every points within the object).

The moment of inertia for several commonly used object will be introduced in this section.

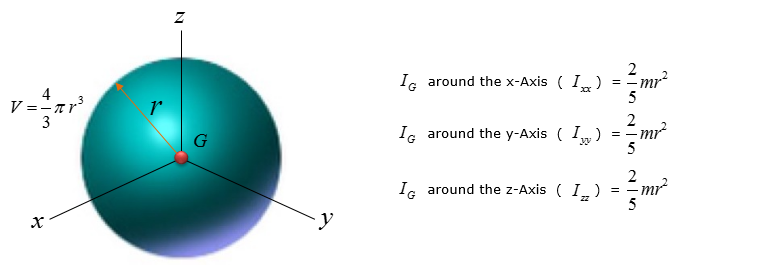
< Sphere >

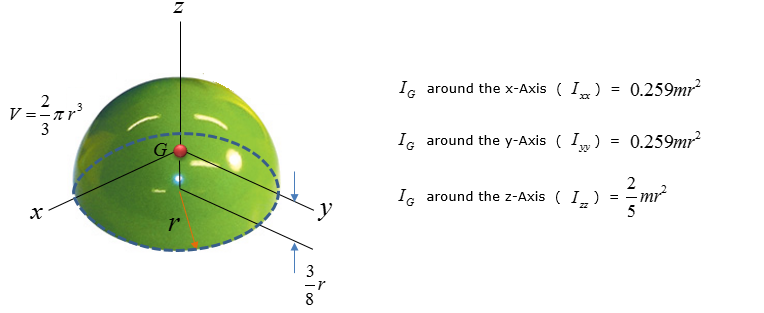
< Hemi Sphere >

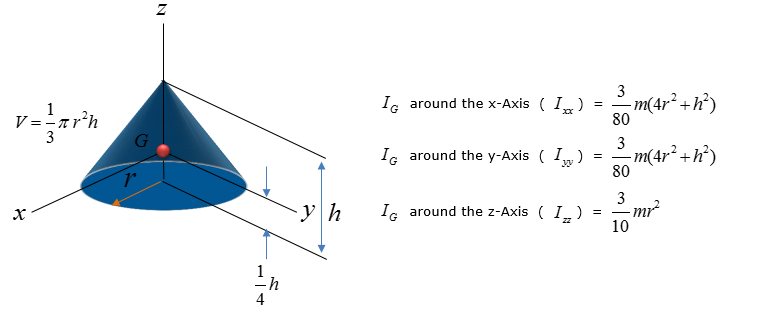
< Cone >

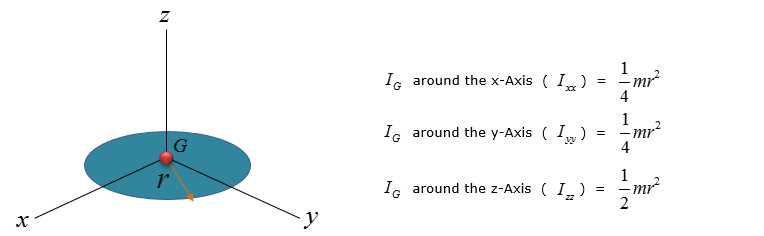
< Thin Circular Disk >

< Slender Rod >

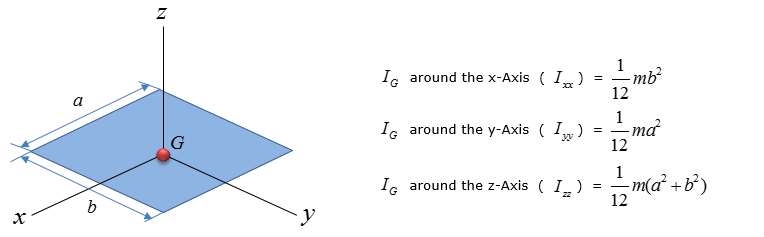
< Thin Plate >

Reference

[1] Moment of Innertia (Hyperphysics)