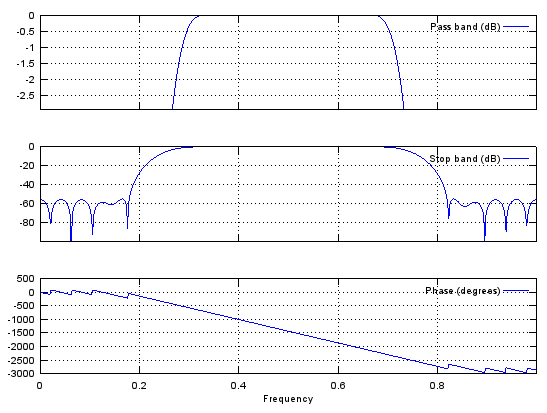
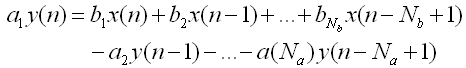Octave/Matlab                                                 Home : www.sharetechnote.com

 

 

In this page, I would post a quick reference for Matlab and Octave. (Octave is a GNU program which is designed to provide a free tool that work like Matlab. I don't think it has 100% compatability between Octave and Matlab, but I noticed that most of basic commands are compatible. I would try to list those commands that can work both with Matlab and Octave). All the sample code listed here, I tried with Octave, not with Matlab.

 

There are huge number of functions which has not been explained here, but I would try to list those functions which are most commonly used in most of matlab sample script you can get. My purpose is to provide you the set of basic commands with examples so that you can at least read the most of sample script you can get from here and there (e.g, internet) without overwhelming you. If you get familiar with these minimal set of functionality, you would get some 'feeling' about the tool and then you would make sense out of the official document from Mathworks or GNU Octave which explains all the functions but not so many examples.

 

I haven't completed 'what I think is the minimum set' yet and I hope I can complete within a couple of weeks. Stay tuned !!!

 

 

Vector (One Dimmensional Array)

 

 

Matrix (Two or Higher Dimmensional Array)

 

 

Random Number Generation

 

 

2D Graph

 

 

3D Graph

 

Plot Applications

 

 

Signal Processing

 

 

Vector (One Dimmensional Array)

 

< Creating a vector >

 

Method 1 :  v = [ value value value value ...]

 

Ex)

Input

v = [ 1 2 4 7 2 1]

Output

v =

   1   2   4   7   2   1

 

 

Method 2 :  v = start:step:end

 

Ex)

Input

v=1:0.2:2

Output

v =

    1.0000    1.2000    1.4000    1.6000    1.8000    2.0000

 

 

< Creating a vector with linspace >

 

Method 1 :  v = linspace(start_value,end_value,num_of_data)

 

Ex)

Input

v = linspace(1,4,10)

Output

v =

   1.0000   1.3333   1.6667   2.0000   2.3333   2.6667   3.0000   3.3333   3.6667   4.0000

 

 

< Mathematical Operation >

 

Case 1 :  v = vector1 + vector2

 

Ex)

Input

v1=[1 2 3 4];

v2=[5 6 7 8];

v=v1 + v2

Output

v =

    6    8   10   12

 

 

Case 2 :  v = vector1 - vector2

 

Ex)

Input

v1=[1 2 3 4];

v2=[5 6 7 8];

v=v1 - v2

Output

v =

    -4    -4   -4   -4

 

 

Case 3 :  v = vector1 . vector2 (Inner Product)

 

Ex)

Input

v1=[1 2 3 4];

v2=[5 6 7 8];

v=v1 * v2' // Note : I put the transpose operator (') here. Try v = v1*v2 and see what happen.

Output

v =

    70

 

 

Case 4 :  v = vector1 x vector2 (multiplication of each elements)

 

Ex)

Input

v1=[1 2 3 4];

v2=[5 6 7 8];

v=v1 .* v2 // Note : I used .*, not * . Try v = v1*v2 and see what happen.

Output

v =

    5   12   21   32

 

 

Case 5 :  v = vector1 / vector2 (division of each elements)

 

Ex)

Input

v1=[1 2 3 4];

v2=[5 6 7 8];

v=v1 ./ v2 // Note : I used ./, not / 

Output

v =

     0.20000   0.33333   0.42857   0.50000

 

 

Case 6 :  v = scalar + vector2

 

Ex)

Input

v1 =[1 2 3 4];

s = 2;

v= s + v1 // Note : In this case, v = s .+ v1 will give the same result

Output

v =

     3   4   5   6

 

 

Case 7 :  v = scalar x vector2

 

Ex)

Input

v1 =[1 2 3 4];

s = 2;

v= s .* v1  // Note : In this case, v = s * v1 will give the same result

Output

v =

     2   4   6   8

 

 

< Applying functions >

 

Case 1 :  v = function(vector)

 

Ex)

Input

v1 =[1 2 3 4];

v= sin(v1) 

Output

v =

     0.84147   0.90930   0.14112  -0.75680

 

 

Ex)

Input

v1 =[1 2 3 4];

v= v1.^2 + 2 .* v1 + cos(v1)

Output

v =

     3.5403    7.5839   14.0100   23.3464

 

 

< Referencing the elements >

 

Case 1 :  v = vector (index)

 

Ex)

Input

v1 =[1 2 3 4];

v= v1(3)

Output

v =

     3

 

 

Case 2 :  v = vector ([index range])

 

Ex)

Input

v1 =[1 2 3 4];

v= v1([1:3])

Output

v =

     1 2 3

 

 

Case 3 :  v = vector ([index list])

 

Ex)

Input

v1 =[1 2 3 4];

v= v1([4 2 3])

Output

v =

     4 2 3

 

 

Case 4 :  v = vector (end)

 

Ex)

Input

v1 =[1 2 3 4];

v= v1(end)

Output

v =

     4

 

 

< Concatenating Vectors >

 

Case 1 :  v = [v1 v2] // All the logic is same

 

Ex)

Input

v1 =[1 2 3 4];

v2 =[5 6 7 8];

v= [v1 v2]

Output

v =

      1   2   3   4   5   6   7   8

 

 

Ex)

Input

v1 =[1 2 3 4];

v2 =[5 6 7 8];

v= [v1 v2 -v1]

Output

v =

      1   2   3   4   5   6   7   8  -1  -2  -3  -4

 

 

Ex)

Input

v=[];   // create a variable named 'v' and initialize it with an empty array

for i = 1:10

      v=[v i];

end

v

Output

v =

      1   2   3   4   5   6   7   8   9  10

 

 

< Rearranging Elements - shift() >

 

Case 1 : v = shift(vector,N) // Where N is a Positive Number

 

Ex)

Input

v1 = [1 2 3 4 5 6 7 8 9 10];

v = shift(v1,3)

Output

v =

         8    9   10    1    2    3    4    5    6    7

 

 

Case 2 : v = shift(vector,N) // Where N is a Negative Number

 

Ex)

Input

v1 = [1 2 3 4 5 6 7 8 9 10];

v = shift(v1,-3)

Output

v =

         4    5    6    7    8    9   10    1    2    3

 

 

< Getting the size of a vector : size() >

 

Case 1 : v = size(v) // returns number of cols and number of rows of v

 

Ex)

Input

t = 0:0.1:10;

size(t)

Output

ans =

     1   101

 

 

Case 2 : v = size(v,1) // returns the number of rows of v

 

Ex)

Input

t = 0:0.1:10;

size(t,1)

Output

ans =

     1  

 

 

Case 3 : v = size(v,2) // returns the number of rows of v

 

Ex)

Input

t = 0:0.1:10;

size(t,2)

Output

ans =

     101

 

 

< Getting the size of a vector : length() >

 

Case 1 : v = length(v) // returns number of elements of v

 

Ex)

Input

t = 0:0.1:10;

length(t)

Output

ans =

     101

 

 

 

< Converting a Vector into a Matrix (Converting one dimmensional array into multi dimensional array) >

 

Case 1 : v = reshape(vector,rows,cols)

 

Ex)

Input

v1 = [1 2 3 4 5 6 7 8 9 10];

v = reshape(v1,2,5)  // Note : Number of matrix elements and Vector elements should be same

Output

v =

         1   2   3   4   5

         6   7   8   9  10

 

 

Matrix (Two or Higher Dimmensional Array)

 

 

< Creating a Matrix >

 

Method 1 :  m = [ value value value ; value value value ;  ...]

 

Ex)

Input

 m = [1 2 3; 4 5 6; 7 8 9]

Output

 m =

   1   2   3

   4   5   6

   7   8   9

 

 

Method 2 :  m = [ vector ; vector ;  ...]

 

Ex)

Input

v1 = [1 2 3];

v2 = [4 5 6];

v3 = [7,8,9];

m = [v1; v2; v3]

Output

 m =

   1   2   3

   4   5   6

   7   8   9

 

 

< Creating an Identity Matrix >

 

Method 1 :  m = eye(M) // M x M identity matrix

 

Ex)

Input

 m = one(3)

Output

 m =

   1   0   0

   0   1   0

   0   0   1

 

 

< Creating M x N Zero Matrix >

 

Method 1 :  m = zeros(M,N)

 

Ex)

Input

 m = zeros(4,2)

Output

 m =

   0   0

   0   0

   0   0

   0   0

 

 

Method 2 :  m = zeros(M) // M x M square matrix

 

Ex)

Input

 m = zeros(3)

Output

 m =

   0   0   0

   0   0   0

   0   0   0

 

 

< Creating a M x N one matrix >

 

Method 1 :  m = ones(M,N)

 

Ex)

Input

 m = ones(4,2)

Output

 m =

   1   1

   1   1

   1   1

   1   1

 

 

Method 2 :  m = ones(M) // M x M square matrix

 

Ex)

Input

 m = one(3)

Output

 m =

   1   1   1

   1   1   1

   1   1   1

 

 

< Mathematical Operation >

 

Case 1 : m = matrix1 + matrix 2;

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m2 = [9 8 7; 6 5 4; 3 2 1];

m = m1 + m2

Output

 m =

   10   10   10

   10   10   10

   10   10   10

 

 

Case 2 : m = matrix1 .* matrix 2; // element by element multiplication

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m2 = [9 8 7; 6 5 4; 3 2 1];

m = m1 .* m2

Output

 m =

    9   16   21

   24   25   24

   21   16    9

 

 

Case 3 : m = matrix1 * matrix 2; // Inner Product

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m2 = [9 8 7; 6 5 4; 3 2 1];

m = m1 * m2

Output

 m =

    30    24    18

    84    69    54

   138   114    90

 

 

Case 4 : m = matrix1 .^ n; // power of n for each element

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m2 = [9 8 7; 6 5 4; 3 2 1];

m = m1 .^ 2;

Output

 m =

    1    4    9

   16   25   36

   49   64   81

 

 

Case 5 : m = matrix1 ^ n; // matrix power

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m2 = [9 8 7; 6 5 4; 3 2 1];

m = m1 ^ 2;

Output

 m =

    30    36    42

    66    81    96

   102   126   150

 

 

Case 6 : tm = m'; // transpose matrix

 

Ex)

Input

m = [1 2 3; 6 5 4; 7 3 9];

tm=m'

Output

 tm =

     1   6   7

     2   5   3

     3   4   9

 

 

Case 7 : im = inv(m); // take the inverse matrix

 

Ex)

Input

m = [1 2 3; 6 5 4; 7 3 9];

im=inv(m)

Output

im = 

  -0.47143   0.12857   0.10000

   0.37143   0.17143  -0.20000

   0.24286  -0.15714   0.10000

 

 

Case 8 : im = det(m); // take the determinant of the matrix

 

Ex)

Input

m = [1 2 3; 6 5 4; 7 3 9];

dm=det(m)

Output

dm = 

  -70

 

 

< Matrix Operators >

 

Case 1 : Eigenvalue and Eigenvector

 

Ex)

Input

A = [1.01 0;0 0.9];

[v,d]=eig(A)

Output

v =

 

   0   1

   1   0

 

d =

 

Diagonal Matrix

 

   0.90000         0

         0   1.01000

Input

A*v

Output

ans =

 

   0.00000   1.01000

   0.90000   0.00000

Input

v*d

Output

ans =

 

   0.00000   1.01000

   0.90000   0.00000

 

 

 

 

< Rearranging Elements - circshift() >

 

Case 1 : m = circshift(m1,N) // Where N is a positive Number. This shift rows

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = circshift(m1,1)

Output

 m =

    7   8   9

    1   2   3

    4   5   6

 

 

Case 2 : m = circshift(m1,N) // Where N is a Negative Number. This shift rows

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = circshift(m1,-1)

Output

 m =

   4   5   6

   7   8   9

   1   2   3

 

 

Case 3 : m = circshift(m1,[0 N]) // Where N is a Positive Number. This shift cols

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = circshift(m1,[0 1])

Output

 m =

   3   1   2

   6   4   5

   9   7   8

 

 

Case 3 : m = circshift(m1,[0 N]) // Where N is a Negative Number. This shift cols

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = circshift(m1,[0 1])

Output

 m =

   2   3   1

   5   6   4

   8   9   7

 

 

< Rearranging Eelemetns - resize() >

 

Case 1 : m = resize(m1,M,N,..)

// Resize Matrix m1 to be an M x N x .. matrix, where M, N is smaller than the original matrix

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = resize(m1,3,2)

Output

 m =

   1   2

   4   5

   7   8

 

 

Case 2 : m = resize(m1,M,N,..)

// Resize Matrix m1 to be an M x N x .. matrix, where M or N is smaller than the original matrix

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = resize(m1,3,2)

Output

 m =

   1   2   3   0   0

   4   5   6   0   0

   7   8   9   0   0

   0   0   0   0   0

 

 

Case 3 : m = resize(m1,M) // Resize Matrix m1 to be an M x M  matrix

 

Ex)

Input

m1 = [1 2 3; 4 5 6; 7 8 9];

m = resize(m1,2)

Output

 m =

   1   2   

   4   5  

 

 

 

Random Number Generation

 

< Single Random Number between 0 and 1 >

 

Case 1 : r = rand(1,1)

 

Ex)

Input

r = rand(1,1);

Output

r =

         0.36579

 

 

< Single Random Number between a and b >

 

Case 1 : r = a + (b-a)*rand(1,1)

 

Ex)

Input

a = 2;

b = 5;

r = a + (b-a)*rand(1,1)

Output

r =

         2.36579

 

 

< N Random Number between 0 and 1 >

 

Case 1 : r = rand(1,N)

 

Ex)

Input

r = rand(1,5);

Output

r =

         0.199260   0.814680   0.687995   0.666070   0.013624

 

 

< N Random Number between a and b >

 

Case 1 : r = a + (b-a)*rand(1,N)

 

Ex)

Input

a = 2;

b = 5;

r = a + (b-a)*rand(1,5)

Output

r =

         2.6419   4.1258   4.7051   2.0323   3.4711

 

 

< Single Random Integer between 0 and N >

 

Case 1 : r = randi(N)

 

Ex)

Input

r = randi(10);

Output

r =

         5

 

 

< Single Random Integer between a and b >

 

Case 1 : r = randi([a b]) // where a and b are all integer

 

Ex)

Input

r = randi([100 200]);

Output

r =

         163

 

 

< N Random Number between 0 and M >

 

Case 1 : ri = randi(M,1,N)

 

Ex)

Input

r = randi(100,1,10);

Output

r =

          20   39   63   81   67   54   34   16   93   19

 

 

< N Random Number between a and b >

 

Case 1 : ri = randi([a b],1,N)

 

Ex)

Input

r = randi([100 200],1,10);

Output

r =

          150   114   142   189   172   103   190   102   196   194

 

 

2D Graph

 

< Plot only one data set (y axis data only) >

 

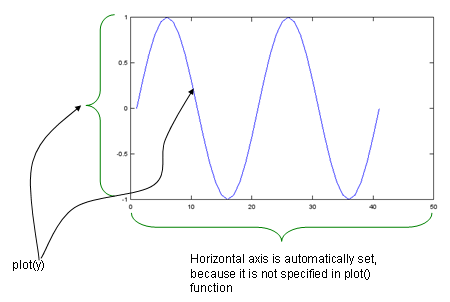
Case 1 : plot(y); // specify y (independent variable) only

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(y);

Output

 

 

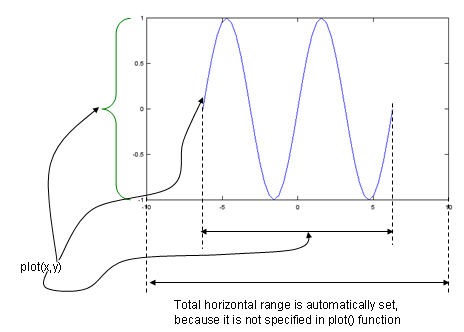
< Plot a set of data ((x,y) sequence) >

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y);

Output

 

 

< x,y Axis Range >

 

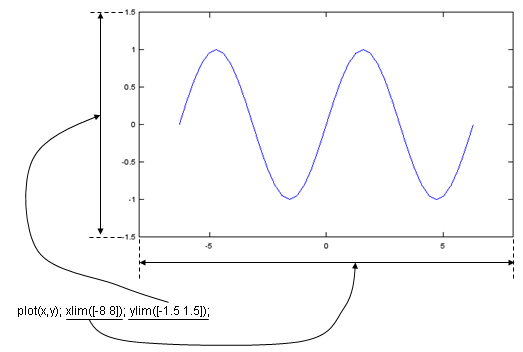
Case 1 : xlim([xmin xmax]); ylim([ymin ymax]);

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y); xlim([-8 8]); ylim([-1.5 1.5]);

Output

 

 

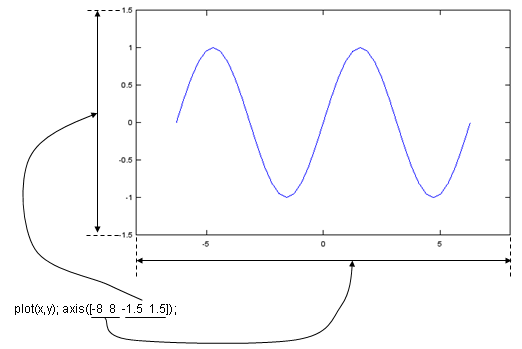
Case 2 : axis([xmin xmax ymin ymax]);

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y); axis([-8 8 -1.5 1.5]);

Output

 

 

< Graph Title, Axis Label >

 

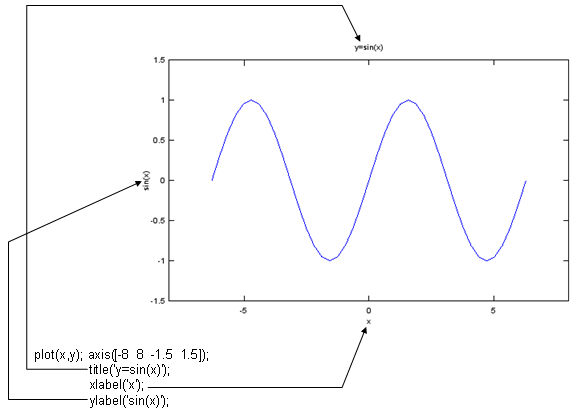
Case 1 : title('text');

            xlabel('text');

            ylabel('text');

 

Ex)

Input

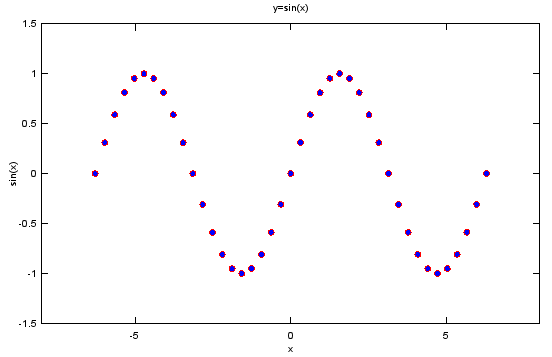
x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y); xlim([-8 8]); ylim([-1.5 1.5]);title('y=sin(x)'); xlabel('x');ylabel('sin(x)');

Output

 

 

< Graph Format and Color >

 

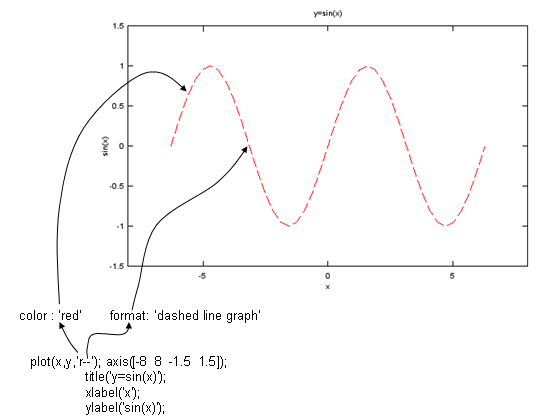
Case 1 : plot(x,y,'format');

    `-'  : solid line.

    `.'  : dotted line.

    `--' : dashed line

    `^'  : triangular mark

    `+'  : + mark

    `*'  : * mark

    `o'  : o (circle) mark

    `x'  : x mark

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y,'r--'); xlim([-8 8]); ylim([-1.5 1.5]);title('y=sin(x)'); xlabel('x');ylabel('sin(x)');

Output

 

 

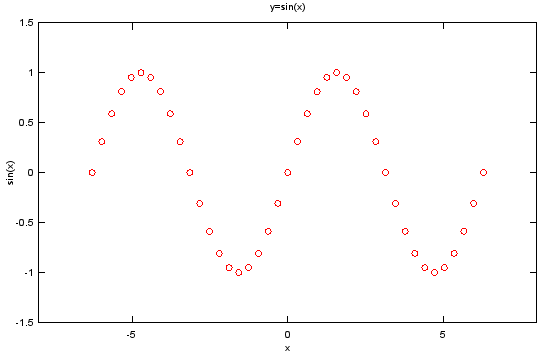
Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y,'ro'); xlim([-8 8]); ylim([-1.5 1.5]);title('y=sin(x)'); xlabel('x');ylabel('sin(x)');

Output

 

 

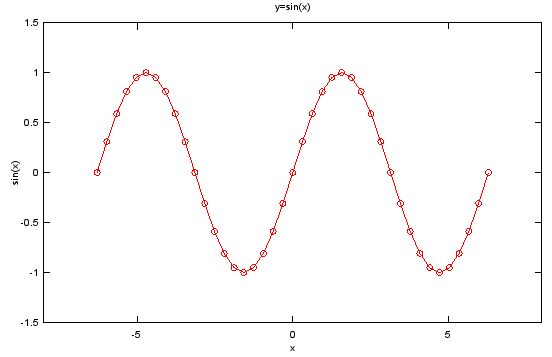
Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y,'ro-'); xlim([-8 8]); ylim([-1.5 1.5]);title('y=sin(x)'); xlabel('x');ylabel('sin(x)');

Output

 

 

< Graph with Filled Marker >

 

Case 1 : MarkerFaceColor,[r g b]  // r,g,b value is range between 0 and 1.

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y=sin(x);

plot(x,y,'ro','MarkerFaceColor',[0 0 1]);

axis([-8 8 -1.5 1.5]);

title('y=sin(x)'); xlabel('x');ylabel('sin(x>< 0 1]);

Output

 

 

< Aspect Ratio >

 

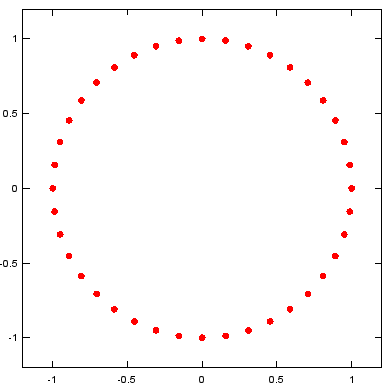
Case 1 : daspect([xratio yratio])

 

Ex)

Input

t=0:2*pi/40:2*pi;

e1 = exp(t*j);

plot(real(e1),imag(e1),'ro','MarkerFaceColor',[1 0 0]); axis([-1.2 1.2 -1.2 1.2]);daspect([1 1]);

Output

 

 

< Multiple Plots in a single graph area using plot >

 

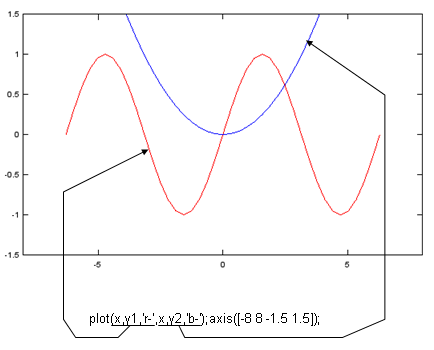
Case 1 : plot(x1,y1,'format1',x2,y2,'format2',...)

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y1=sin(x);

y2=0.1 .* x .^2;

plot(x,y1,'r-',x,y2,'b-');axis([-8 8 -1.5 1.5]);

Output

 

 

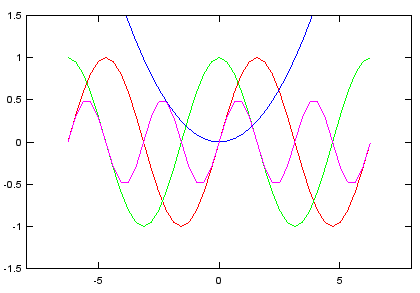
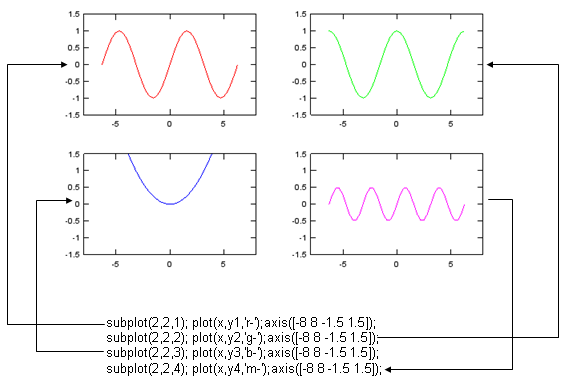
< Multiple Plots in a single graph area using hold on >

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y1=sin(x);

y2=cos(x);

y3=0.1.*x.^2;

y4=sin(x).*cos(x);

subplot(2,2,1); plot(x,y1,'r-');axis([-8 8 -1.5 1.5]);hold on;

subplot(2,2,2); plot(x,y2,'g-');axis([-8 8 -1.5 1.5]);hold on;

subplot(2,2,3); plot(x,y3,'b-');axis([-8 8 -1.5 1.5]);hold on;

subplot(2,2,4); plot(x,y4,'m-');axis([-8 8 -1.5 1.5]);

Output

 

 

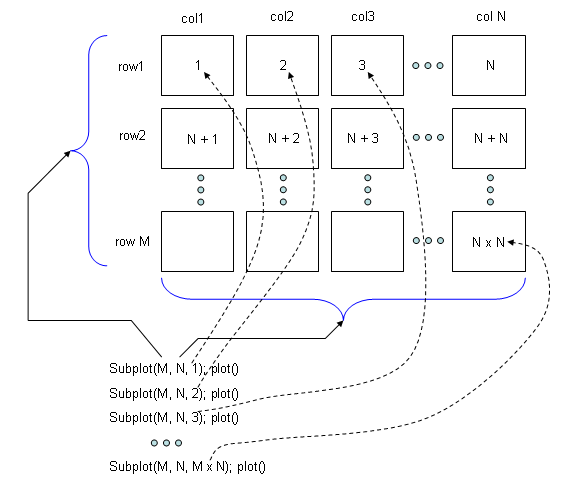
< Multiple Plots in a single graph area using subplot >

 

Case 1 : Subplot(M, N, 1); plot()

            Subplot(M, N, 2); plot()

            Subplot(M, N, 3); plot()

             ...

            Subplot(M, N, M x N); plot()

 

Ex)

Input

x = -2*pi:1/10*pi:2*pi;

y1=sin(x);

y2=cos(x);

y3=0.1.*x.^2;

y4=sin(x).*cos(x);

subplot(2,2,1); plot(x,y1,'r-');axis([-8 8 -1.5 1.5]);

subplot(2,2,2); plot(x,y2,'g-');axis([-8 8 -1.5 1.5]);

subplot(2,2,3); plot(x,y3,'b-');axis([-8 8 -1.5 1.5]);

subplot(2,2,4); plot(x,y4,'m-');axis([-8 8 -1.5 1.5]);

Output

 

 

3D Plot

 

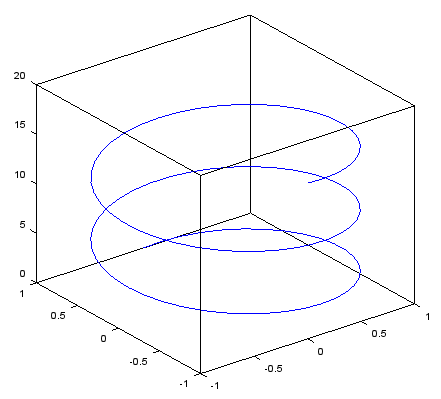
< plot3 - 3D Parametric Plot >

 

Ex)

Input

t = linspace(0,5*pi,100);

plot3(sin(t),cos(t),t)

Output

 

 

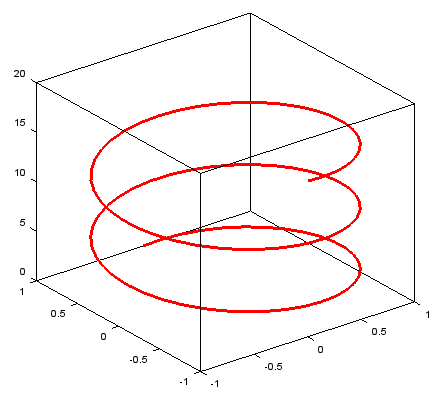
< plot3 - 3D Parametric Plot - linewidth, color>

 

Ex)

Input

t = linspace(0,5*pi,100);

plot3(sin(t),cos(t),t,'linewidth',3,'color','r');

Output

 

 

< plot3 - 3D Parametric Plot - view >

 

view(angle_around_z_axis, angle_around_y_axis) // angle in degree

 

Ex)

Input

t = linspace(0,5*pi,100);

plot3(sin(t),cos(t),t,'linewidth',3,'color','r');

view(-20,80);

Output

 

 

< mesh >

 

Ex)

Input

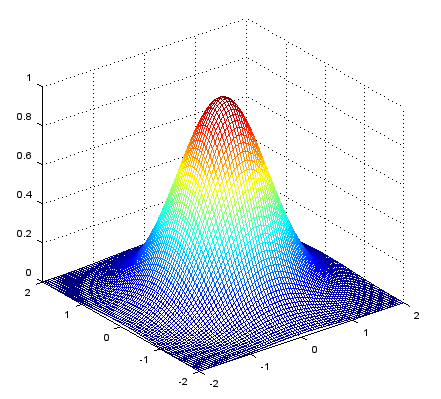
xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

mesh(X,Y,Z);

Output

 

 

< mesh - axis range >

 

axis([xmin xmax ymin ymax zmin zmax])

 

Ex)

Input

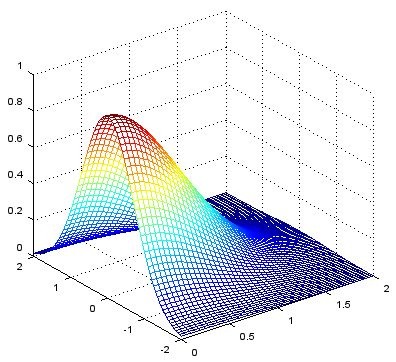
xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

mesh(X,Y,Z); axis([0 2 -2 2 0 1]);

Output

 

 

< surface >

 

Ex)

Input

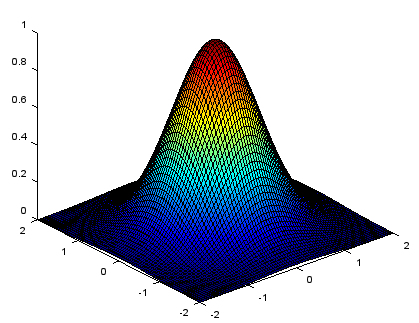
xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

surface(X,Y,Z);

view(-40,30);

Output

 

 

< contour >

 

Ex)

Input

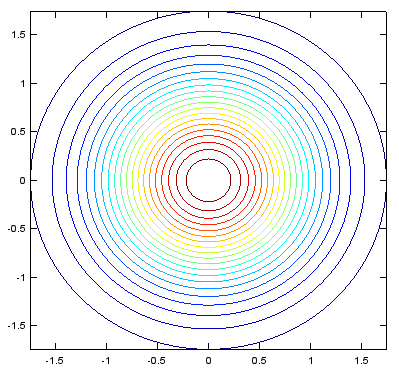
xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

contour(X,Y,Z,20);

Output

 

 

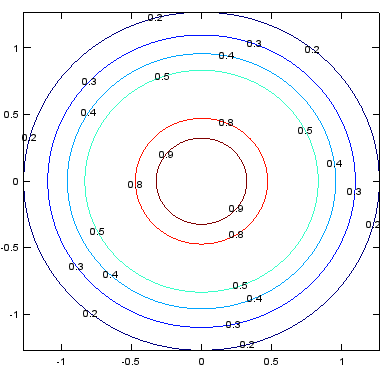
< contour - Labeling the level >

 

Ex)

Input

xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

[c,h]=contour(X,Y,Z,5);

clabel(c,h);

Output

 

 

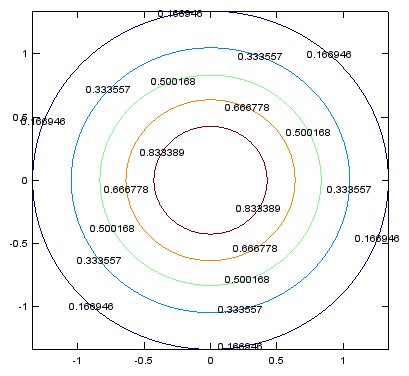
< contour - forcing contour lines >

 

Ex)

Input

xstep = -2:.05:2;

ystep = -2:.05:2;

[X,Y] = meshgrid(xstep,ystep);

Z = exp(-(X.^2+Y.^2));

[c,h]=contour(X,Y,Z,[0.0 0.2 0.3 0.4 0.5 0.8 0.9]);

clabel(c,h);

Output

 

 

< contour - implicit plot >

 

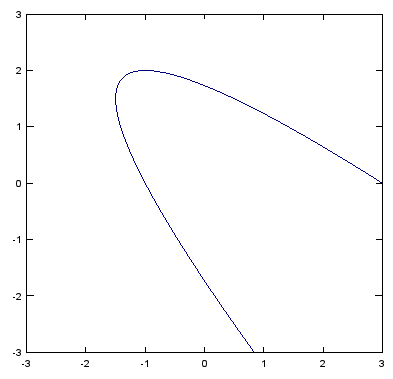
Ex)

Input

xstep = -3:.05:3;

ystep = -3:.05:3;

[X,Y] = meshgrid(xstep,ystep);

Z=X.^2 .+ 2.*X.*Y .+ Y.^2 - 2.*X;

contour(X,Y,Z,[3,3]); % implicit plot for X.^2 .+ 2.*X.*Y .+ Y.^2 - 2.*X = 3

Output

 

 

Plot Application

 

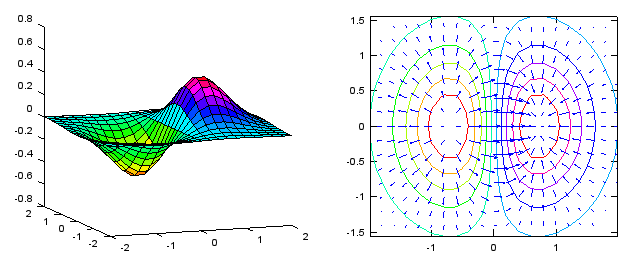
< Vector Plot - Gradient Plot >

 

Ex)

Input

[X,Y] = meshgrid(-2:.2:2);

Z = X.*exp(-X.^2 - Y.^2);

[DX,DY] = gradient(Z,.2,.2);

 

subplot(1,2,1);

surface(X,Y,Z);

view(-20,10);

 

subplot(1,2,2);

contour(X,Y,Z);

hold on

quiver(X,Y,DX,DY);

colormap hsv

hold off

Output

 

 

Signal Processing

 

< Filter >

 

Apply the Digital Filter described as below.  As you see in the mathematical description, you can apply both FIR and IIR applying the tab values.

 

 

Ex)

Input

a = 1;

b = [0.2 0.2 0.2 0.2 0.2];

t = linspace(0,5*pi,100);

x = sin(t) .+ 0.5*rand(1,100);

 

y = filter(b,a,x);

plot(x,'r-',y,'b-');

Output

 

 

< fir1>

 

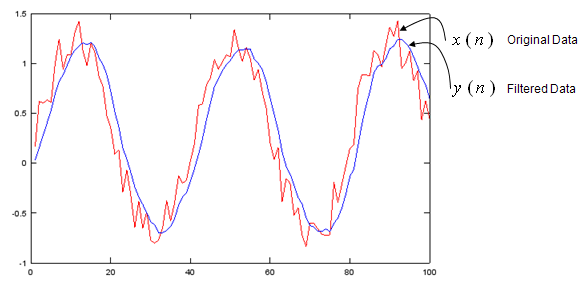
Case 1 : b = fir1(N,[pass_L,pass_R])

// Generate N tap Bandpass Filter with passband [pass_L,pass_R]. 0 < pass_L,pass_R < 1

 

Ex)

Input

b = fir1(48,[0.25 0.75]);

stem(b);

figure;

freqz(b,1,512);

Output

 

 

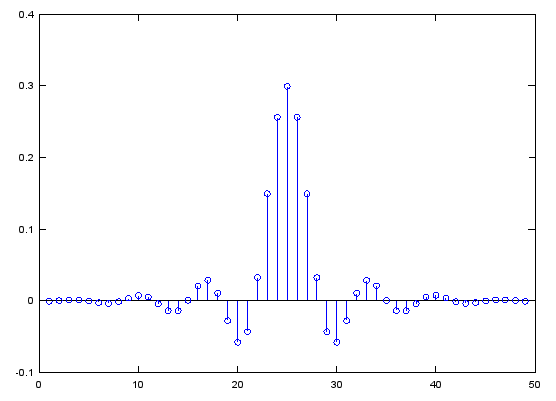
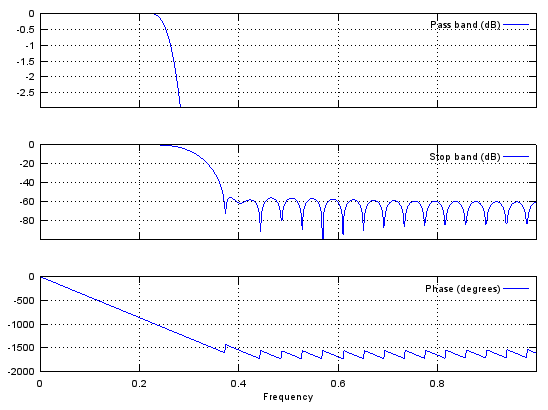
Case 2 : b = fir1(N,pass_R,'low')

// Generate N tap Lowpass Filter with passband [0,pass_R]. 0 < pass_R < 1

 

Ex)

Input

b = fir1(48,0.3,'low');

stem(b);

figure;

freqz(b,1,512);

Output

 

 

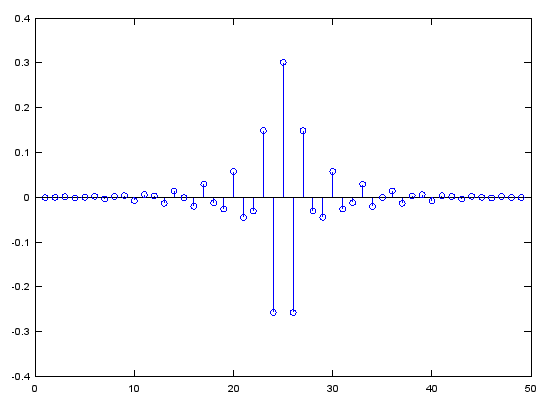
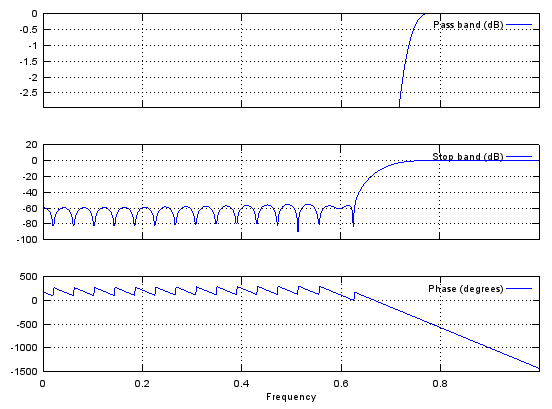
Case 3 : b = fir1(N,pass_L,'high')

// Generate N tap Highpass Filter with passband pass_L. 0 < pass_L < 1

 

Ex)

Input

b = fir1(48,0.7,'high');

stem(b);

figure;

freqz(b,1,512);

Output

 

 

Case 4 : b = fir1(N,[stop_L stop_R],'stop')

// Generate N tap Bandstop Filter with bandstop between stop_L and stop_R. 0 < stop_L, stop_R < 1

 

Ex)

Input

b = fir1(48,[0.45 0.55],'stop');

stem(b);

figure;

freqz(b,1,512);

Output

 

 

< fir2 >

 

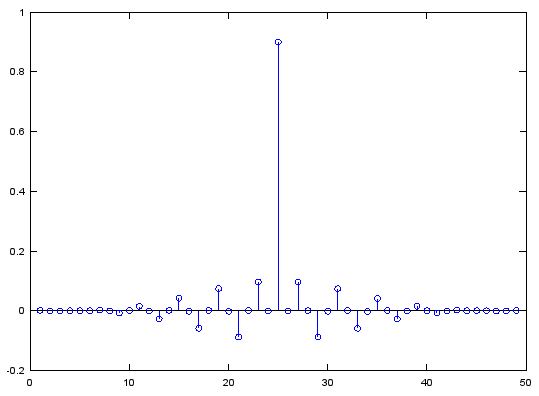
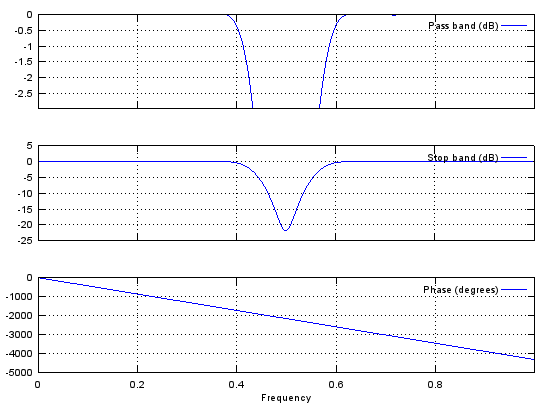
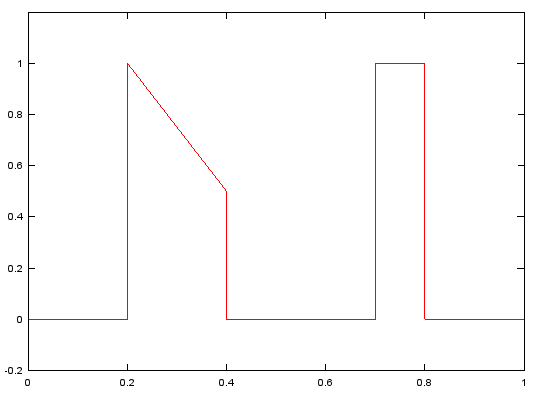
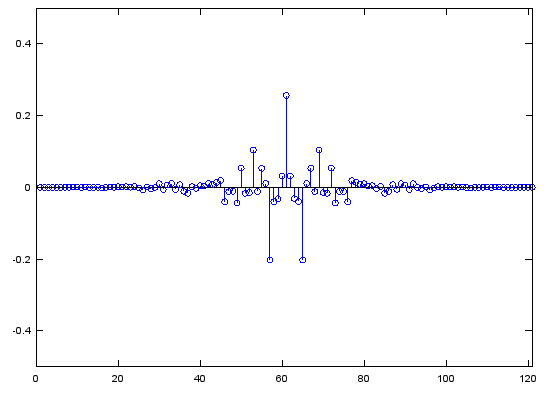
Case 1 : b = fir2(N,[f1,f2,f3,...,fm],[mag1,mag2,mag3,...,magM])

// Generate N tap Filter with aribitrary passband definition specified by [f1,f2,f3,...,fm],[mag1,mag2,mag3,...,magM]

 

Ex)

Input

f=[0, 0.2, 0.2, 0.4, 0.4, 0.7, 0.7, 0.8, 0.8, 1];

m=[0, 0, 1, 1/2, 0, 0, 1, 1, 0, 0];

b=fir2(120,f,m);

 

figure;

plot(f,m,'r-');axis([0 1 -0.2 1.2]);

figure;

stem(b);axis([0,length(b),-0.5,0.5]);

figure;

freqz(b,1,512);

Output

 

 

 

< freqz >

 

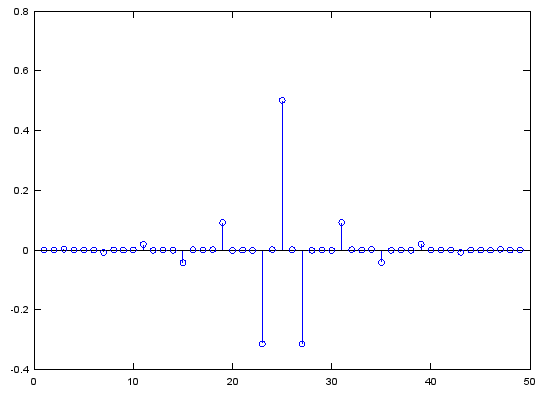
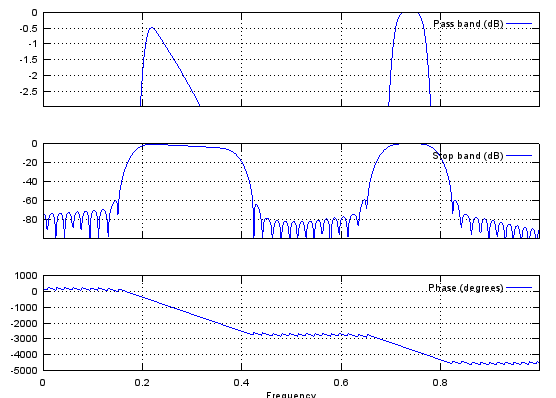
Case 1 : freqz(b,a,NoOfFrequencyPoints)

// Produce frequency response plot (magnitude and phase vs frequency) with IIR filter coefficient vector b and a. (In case of FIR filter, set a to be 1).

 

Ex)

Input

b = fir1(48,[0.25 0.75]);

freqz(b,1,512);

Output

 

 

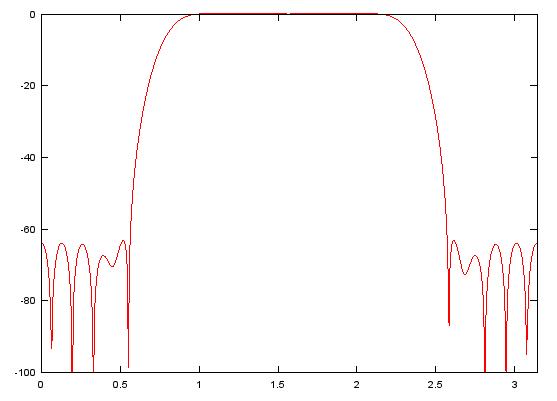
Case 2 : [h,w] = freqz(b,a,NoOfFrequencyPoints)

// return the numerical data of frequency response with IIR filter coefficient vector b and a. (In case of FIR filter, set a to be 1).  h returns the magnitude values and w returns frequency point values.

 

Ex)

Input

b = fir1(48,[0.25 0.75]);

[h,w]=freqz(b,1,512);

plot(w,10 .* log(abs(h)),'r-');axis([0 pi,-100,0]);

Output