Quantum Computing  

 

 

 

Double Slit Experiment

The double-slit experiment is a classic physics experiment that demonstrates the wave-particle duality of matter. This means that particles, such as electrons or photons, can behave as both waves and particles. This is one of the most fundamental concepts in quantum mechanics, and it has many implications for our understanding of the universe.

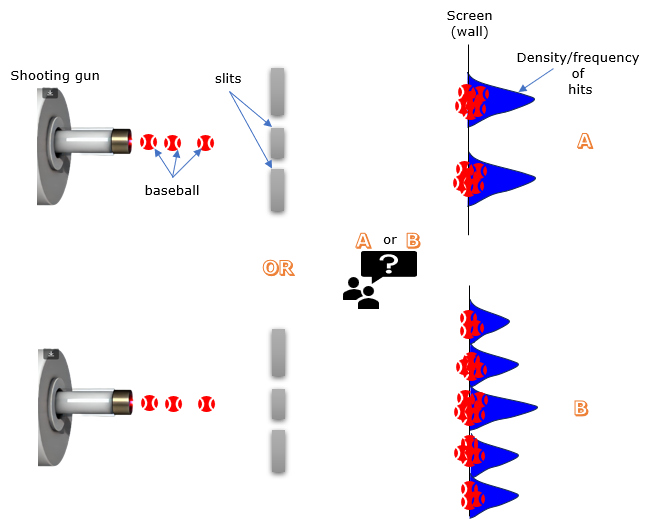
NOTE : If you haven't seen or heard of this experiment before, it would not be easier to picture the setup and concept behind it regardless of how many times you read this part. So my recommendation is for you to go through at least a few YouTube that I listed or any other YouTube video that you find.

Primer before the experiment

Before jumping directly into the details of the double slit experiment, I want to set some baseline to trigger some questions in your mind.

Imagine you're at a baseball game, but instead of a batter at home plate, there's a pitching machine firing off hundreds of baseballs towards a wall with two narrow slits.  Those balls that don't smash into the wall sail through the slits and land on a big screen behind it. Now, imagine carefully marking where each ball lands on that screen. What kind of pattern do you think you'd see? Take a look at the two pictures below – would the marks on the screen look more like Case A or Case B?"

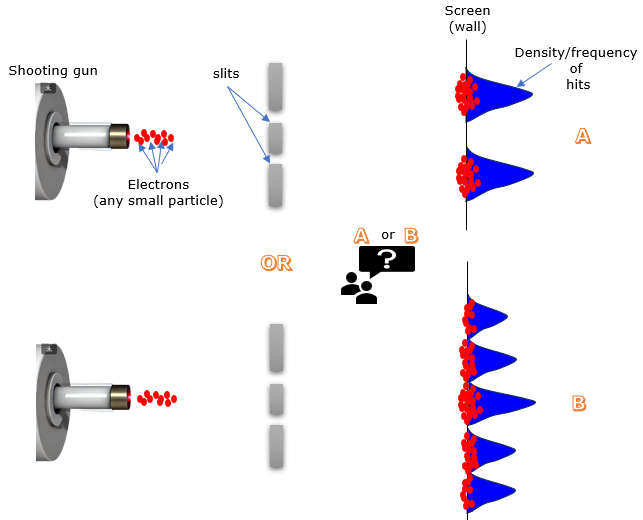
Let's rewind that scene at the ballpark.  The pitching machine is still there, but instead of hurling baseballs, it's now firing a stream of electrons towards the wall with the two slits.  These electrons are incredibly tiny – way smaller than even the tiniest speck of dust you can imagine.

After a while of shooting game, Which one do you think better represents the pattern those electrons would make on the screen? A or B.

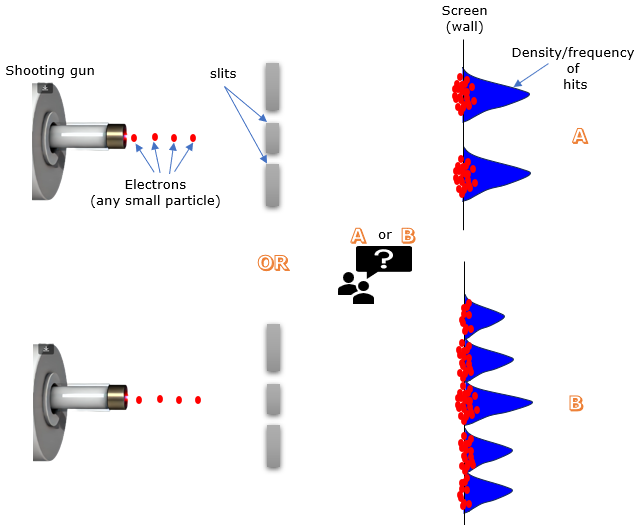
Let's tweak our electron-firing pitching machine one last time. This time, we're going to dial down the intensity way low. So low, in fact, that only one electron gets fired at a time.  Each electron makes its lonely journey towards the wall with the two slits, zips through (somehow!), and eventually hits the screen.

Which one do you think better represents the pattern those electrons would make on the screen? A or B.

I hope you have some questions (or at least a little strange feelings) boggling up in your mind.

Experimental Setup

The double-slit experiment involves a stream of individual particles, like electrons, aimed at a barrier with two closely spaced slits.  Positioned behind this barrier is a sensitive detector screen that records where each particle lands.  Classical physics leads us to expect two distinct clumps of particle impacts aligned with the slits, much like tiny bullets passing through. However, the experiment reveals a pattern of alternating bright and dark bands, characteristic of interfering waves, defying our intuitive understanding of particles and suggesting a deeper, wave-like nature to these individual bits of matter.

NOTE : When we talk about double slit experiment, there are roughly two types. One in more classical situation using a typical wave (like water wave or ligh beam) as the source and the other case in more of quantum mechanical situation using a more of discrete particle (e.g, electrons) as the source. In this note, I am focus more on the experiment in quantum mechanical situation.

Particle Source

The particle source in a double-slit experiment generates a stream of individual particles, such as photons or electrons, directed towards the two slits.  Lasers or electron guns are commonly used, with careful adjustments made to ensure the particles are emitted one at a time and travel in a controlled manner with specific properties like wavelength and coherence. This precise control is crucial for observing quantum effects in the experiment.

Slit Structure

The slit structure in a double-slit experiment is a barrier with two narrow, parallel openings. This barrier can be made from a variety of materials, like thin metal films for photons or silicon nitride membranes for electrons, depending on the type of particle being used. The dimensions of the slits, including their width and the separation between them, are precisely controlled and are typically on the order of micrometers or nanometers. These dimensions are crucial for generating the interference pattern, as they influence the wavelength of the particles and how their wave-like behavior manifests.  The slits themselves need to have sharp edges and be carefully aligned to ensure a clear and accurate interference pattern

Detection Screen

The detection screen in a double-slit experiment acts like a canvas, capturing the arrival points of the particles after they pass through the slits. This screen can take various forms depending on the type of particle involved. For photons, it might be a photographic film, a phosphorescent screen that lights up when struck, or even highly sensitive electronic detectors like CCDs or CMOS sensors. For electrons, a phosphor screen or specialized electron detectors like microchannel plates are used. The key features of a good detection screen are its ability to clearly resolve the fine details of the interference pattern and its sensitivity to individual particle impacts. This allows scientists to observe the wave-like behavior of particles, even when they are sent one by one, revealing the fascinating quantum nature of the world.

Environmental and Experimental Conditions

To ensure the double-slit experiment accurately captures the delicate quantum behavior of particles, it's crucial to control the surrounding environment. For experiments with electrons, this means using a vacuum chamber to eliminate interference from air molecules. Whether using photons or electrons, the setup must be shielded from vibrations and temperature fluctuations that could disrupt the particle stream or the detection screen. Additionally, electromagnetic shielding protects against stray fields that might deflect the particles. These precautions help maintain the integrity of the experiment and ensure that the observed results truly reflect the quantum nature of the particles.

Key Considerations for Successful Experiments

To successfully conduct a double-slit experiment and observe the wonders of quantum mechanics, several key factors need careful attention. First, ensuring the particles are coherent (acting in unison) and have a single wavelength (monochromatic) is crucial for clear interference patterns. This is achieved through high-quality light sources like lasers for photons, and by minimizing energy spread in electron beams.  Second, emitting particles one at a time is essential to demonstrate that individual particles exhibit wave-like behavior. This requires careful control of the particle source intensity.  Finally, precise alignment of all components, including the slits and detectors, is necessary to avoid distortions in the resulting pattern.  Analyzing the data involves careful measurements of the interference fringes and statistical analysis to extract meaningful information from the individual particle detections.

Practical Example of Setup Parameters

The practical setup of double-slit experiments varies significantly depending on the type of particles used, such as photons or electrons, each requiring specific configurations to observe quantum interference.

These tailored setups for photons and electrons exemplify the careful design required to explore the wave-particle duality inherent in quantum mechanics and to reveal the characteristic interference patterns of each type of particle.

Photon Experiment Example

In a photon-based experiment, a Helium-Neon (He-Ne) laser is directed at a pair of slits, etched into a metal-coated glass slide. A CCD camera with a proper pixel size is used to capture the resulting interference pattern.

  • Wavelength (λ): 633 nm (He-Ne laser).
  • Slit Width (a): 10 μm.
  • Slit Separation (d): 50 μm.
  • Material: Metal-coated glass slide.
  • Detector: CCD camera with pixel size of 5 μm.

Electron Experiment Example

For electron-based experiments, more precise control is needed due to the smaller scale of electron wavelengths. Electrons are accelerated, giving them a appropriate de Broglie wavelength. They pass through slits, created in a silicon nitride membrane coated with gold. The electron impacts are detected using a microchannel plate (MCP) coupled to a phosphor screen and a CCD camera, allowing for high-resolution capture of the interference fringes.

  • Acceleration Voltage: 60 kV (electron kinetic energy).
  • De Broglie Wavelength (λ): Approximately 0.005 nm.
  • Slit Width (a): 50 nm.
  • Slit Separation (d): 200 nm.
  • Material: Silicon nitride membrane with gold coating.
  • Detector: MCP coupled to a phosphor screen and CCD camera.

Examples of Double-Slit Experiments with Electrons

The double-slit experiment has been performed with electrons to explore the fundamental nature of quantum mechanics. By varying the electron source and experimental conditions—such as using a continuous stream of electrons, individual electrons, blocking one slit, and more—physicists have observed results that challenge classical expectations. Below are detailed examples of these variations, including the experimental setup, expected results based on classical physics, and the observed quantum mechanical outcomes.

Case 1 : Continuous Stream of Electrons Through Double Slits

The double-slit experiment using a continuous stream of electrons serves as a fundamental illustration of quantum mechanics and the wave-particle duality of matter.

In this setup, the electron gun is firing a steady stream of electrons towards the wall with the two slits.  It's like a microscopic version of a firehose, with countless electrons flowing through the apparatus at once.

Now, since we're firing a continuous stream of electrons – tiny, solid particles – you might reasonably expect to see a pattern like Case A on the screen.  After all, it's easy to picture those electrons as miniature bullets, each one passing through a single slit and hitting the screen directly behind it.  Two slits, two clusters of hits – simple, right?

But here's where the quantum world throws us a curveball.  Instead of that straightforward pattern, what we actually observe is an interference pattern, like Case B!  It's as if those electrons are somehow behaving like waves, spreading out and interfering with each other, even though they're individual particles.  This is one of the core mysteries of the double-slit experiment, and it forces us to reconsider our basic understanding of how matter behaves at the subatomic level.

In this variation, electrons—traditionally considered as discrete particles—are emitted in a steady beam toward a pair of parallel slits. By observing the distribution of electrons on a detection screen beyond the slits, scientists can investigate whether electrons behave like classical particles or exhibit wave-like properties. This experiment not only challenges classical expectations but also provides profound insights into the nature of quantum phenomena, such as interference and superposition, highlighting the inherent "weirdness" of the quantum world.

  • Experimental Setup
    • Electron Source: An electron gun emits a continuous beam of electrons toward a double-slit apparatus.
    • Slit Structure: Two parallel slits of equal width, separated by a small gap, are fabricated on an opaque barrier.
    • Slit Width (a): Approximately 50 nanometers (nm).
    • Slit Separation (d): Approximately 200 nm.
    • Detection Screen: A phosphorescent screen or an electron-sensitive detector placed behind the slits records the impact positions of the electrons.
  • Expected Result (Classical Physics)
    • Classical Prediction: Electrons are particles; thus, they should travel in straight lines through the slits and form two distinct impact regions on the detection screen, corresponding to the positions directly behind each slit.
    • Pattern: Two bright spots or bands aligned with the slits, without any interference effects.
  • Observed Result
    • Interference Pattern: Instead of two distinct regions, a series of alternating bright and dark fringes (interference pattern) appears on the detection screen.
    • Wave-Like Behavior: The pattern resembles that produced by waves interfering constructively and destructively.
    • Implication: Electrons exhibit wave-like properties, even though they are particles.
  • Explanation
    • Quantum Mechanics: Electrons have a wavefunction that describes a probability amplitude. When passing through both slits, their wavefunctions interfere, leading to the observed pattern.
    • Wave-Particle Duality: Electrons cannot be described solely as particles; they also possess wave characteristics.

Case 2 : Individual Electrons Through Double Slits

Now Imagine we slow down our electron gun so much that it only fires one electron at a time.  Each electron makes a solitary journey towards the wall, passes through the slits, and eventually hits the detection screen.

Now, common sense would tell you that each electron can only go through ONE of the slits, right? After all, it's a single, indivisible particle. And if that's the case, you'd expect to see a pattern like Case A build up over time – two distinct clusters of hits corresponding to the two slits.

But here's where the quantum world throws our intuition out the window.  Even when we send those electrons one by one, what we see on the screen is... still the interference pattern, Case B!  It's as if each individual electron somehow knows about BOTH slits and interferes with itself to create those alternating bands of bright and dark areas.

This is perhaps the most baffling aspect of the double-slit experiment. It suggests that electrons, even though they seem like tiny particles, also behave like waves that can spread out and interfere with themselves.  It challenges our very notion of what it means for something to be a "particle" in the first place.

This single-electron version of the experiment really drives home the central mystery of quantum mechanics: the wave-particle duality of matter. It forces us to confront the fact that the subatomic world operates under very different rules than the ones we're used to in our everyday lives.

The double-slit experiment using individual electrons provides one of the most compelling demonstrations of quantum mechanics and the counterintuitive nature of the quantum world. In this variation, electrons are emitted one at a time toward a pair of narrowly spaced slits, ensuring that each electron traverses the apparatus in complete isolation. Classical physics predicts that these discrete particles should pass through one slit or the other and form two distinct impact patterns on the detection screen. However, the observed results defy this expectation: over time, as numerous individual electrons are detected, an interference pattern emerges on the screen—characteristic of wave-like behavior. This phenomenon suggests that each electron simultaneously explores all possible paths, effectively interfering with itself, and highlights fundamental quantum principles such as superposition and wave-particle duality. The experiment underscores the inherent "weirdness" of quantum mechanics, challenging our traditional notions of particles and emphasizing the profound differences between classical and quantum realms.

  • Experimental Setup
    • Electron Source: The electron gun is adjusted to emit electrons one at a time, ensuring that each electron is isolated in time as it approaches the slits.
    • Slit Structure: Same as before—double slits with nano-scale dimensions.
    • Detection Screen: A sensitive detector capable of recording single-electron events.
  • Expected Result (Classical Physics)
    • Classical Prediction: Each electron, as a particle, should pass through one slit or the other and impact the detection screen accordingly.
    • Pattern Over Time: Accumulated impacts should form two distinct bands corresponding to the two slits, as there is no possibility for interference with other electrons.
  • Observed Result
    • Gradual Formation of Interference Pattern: Individual electrons hit the detection screen at seemingly random positions. However, as more electrons are recorded, an interference pattern emerges over time.
    • Self-Interference: Each electron behaves as if it interferes with itself, even though it is alone.
  • Explanation
    • Superposition Principle: Before measurement, the electron's wavefunction encompasses all possible paths, including passing through both slits simultaneously.
    • Collapse Upon Detection: The act of detection localizes the electron, but the cumulative impact positions reveal the underlying wave nature.

Case 3 : Blocking One Slit

The "Blocking One Slit" variation of the double-slit experiment serves as a fundamental test to contrast classical and quantum behaviors of particles like electrons or photons. In this setup, one of the two slits in the double-slit apparatus is physically obstructed, allowing particles to pass through only a single narrow opening. Classical physics predicts that particles traveling through the open slit should produce a straightforward distribution pattern directly behind it, akin to bullets passing through a hole. However, quantum mechanics reveals a more nuanced reality: even with one slit blocked, particles exhibit a diffraction pattern characteristic of wave-like behavior. This phenomenon arises from the wave nature of particles spreading out after passing through the narrow aperture, resulting in a broader distribution on the detection screen with a central maximum and diminishing side fringes. By examining the differences between the single-slit and double-slit outcomes, this experiment highlights the principles of wave-particle duality and underscores how the presence or absence of multiple paths affects interference patterns. It provides critical insights into quantum superposition and the inherent "weirdness" of quantum mechanics, challenging our classical intuitions about how particles should behave.

  • Experimental Setup
    • Modification: One of the two slits is physically blocked or closed.
    • Electron Source: Can be either a continuous stream or individual electrons.
    • Detection Screen: Remains unchanged.
  • Expected Result (Classical and Quantum Physics)
    • Classical Prediction: With only one slit open, electrons pass through the single slit and impact the detection screen, forming a pattern directly behind the open slit.
    • Quantum Prediction: A single-slit diffraction pattern should appear, characterized by a central maximum and diminishing side fringes due to wave diffraction.
  • Observed Result
    • Single-Slit Diffraction Pattern: The detection screen shows a broader central maximum with less pronounced side fringes compared to the double-slit interference pattern.
    • No Interference Pattern: The absence of the second slit eliminates the possibility of interference between paths through different slits.
  • Explanation
    • Wave Diffraction: Even with one slit, the electron's wavefunction spreads out after passing through the slit, causing diffraction effects.
    • Particle Behavior: The results align with both classical particle expectations (electrons pass through the open slit) and quantum wave behavior (diffraction occurs).

Case 4 : Introducing Which-Slit Detectors

The "Introducing Which-Slit Detectors" variation of the double-slit experiment explores one of the most perplexing aspects of quantum mechanics: the role of observation in determining the behavior of quantum particles. In this setup, detectors are placed near the slits to ascertain which slit each particle—such as an electron or photon—passes through as it travels toward the detection screen. Classical physics would predict that merely observing the particles should not influence their trajectories or the overall outcome of the experiment. However, the observed results defy this expectation: when which-slit information is obtained, the interference pattern characteristic of wave-like behavior disappears, and instead, particles distribute themselves on the detection screen in a pattern consistent with classical particles passing through one slit or the other. This dramatic change underscores the profound impact of measurement in quantum mechanics, demonstrating how the act of observation collapses the particle's wavefunction and alters its behavior. The experiment highlights fundamental quantum principles such as the observer effect and the complementarity between wave and particle natures, further emphasizing the inherent "weirdness" of the quantum world and challenging our conventional understanding of reality.

  • Experimental Setup
    • Which-Slit Detector: Devices (e.g., light beams, magnetic fields) are placed near the slits to detect which slit an electron passes through without significantly disturbing its path.
    • Electron Source: Individual electrons are emitted toward the double slits.
    • Detection Screen: Same as before.
  • Expected Result (Classical and Naïve Quantum Prediction)
    • Classical Prediction: Detecting which slit the electron passes through should not affect its trajectory; the interference pattern should persist.
    • Naïve Quantum Prediction: One might expect that since the electrons are still going through both slits, interference should occur regardless of observation.
  • Observed Result
    • Disappearance of Interference Pattern: The interference fringes vanish, and the detection screen shows two distinct impact regions corresponding to the two slits.
    • Particle-Like Behavior: Electrons behave as classical particles when which-path information is known.
  • Explanation
    • Observer Effect: Measuring which slit the electron passes through collapses its wavefunction into a definite state.
    • Quantum Decoherence: The act of observation introduces interactions that disturb the electron's phase relationships necessary for interference.
    • Complementarity Principle: Knowledge of the particle's path and the ability to observe interference patterns are mutually exclusive.

Case 5 : Varying Electron Spin States

The "Varying Electron Spin States" variation of the double-slit experiment extends the exploration of quantum mechanics by examining how a particle's intrinsic properties—specifically, its spin—affect interference patterns. In this setup, electrons are prepared with controlled spin orientations using magnetic fields or spin filters before they approach the double slits. Classical physics posits that an electron's spin, being an internal degree of freedom, should not influence its spatial motion or the resulting interference pattern on the detection screen. However, quantum mechanics predicts a more complex interaction: manipulating the spin states can entangle the electron's spin with its path through the slits. This entanglement can alter or even erase the interference pattern, depending on the degree to which the spin states provide which-path information. By observing how changes in spin states impact the interference pattern, this experiment highlights the profound role of quantum entanglement and superposition in determining the behavior of quantum particles. It underscores the non-classical correlation between a particle's internal properties and its spatial trajectory, offering deeper insights into the inherent "weirdness" of the quantum world and challenging our conventional understanding of particle behavior.

  • Experimental Setup
    • Electron Spin Manipulation: Electrons are prepared in specific spin states using magnetic fields (Stern-Gerlach apparatus) before reaching the slits.
    • Spin-Dependent Slits: Slits are designed to interact differently with electrons based on their spin orientation.
    • Electron Source: Emits electrons with controlled spin states.
    • Detection Screen: Capable of detecting spin-dependent outcomes.
  • Expected Result
    • Classical Prediction: Electron spin should not affect the spatial interference pattern, as spin and spatial motion are independent.
    • Quantum Prediction: Manipulating spin states could affect the interference pattern due to entanglement between spin and spatial degrees of freedom.
  • Observed Result
    • Modification of Interference Pattern: The interference pattern changes depending on the spin state of the electrons.
    • Entanglement Effects: If spin states are entangled with the path, observing spin effectively provides which-path information, reducing or eliminating interference.
  • Explanation
    • Quantum Entanglement: The electron's spin state becomes entangled with its path through the slits.
    • Reduced Coherence: Entanglement with spin states introduces decoherence in the spatial degree of freedom.
    • Controlled Interference: By manipulating spin, researchers can control the visibility of the interference pattern.

Case 6 : Quantum Eraser Experiment with Electrons

The "Quantum Eraser Experiment with Electrons" is a profound extension of the classic double-slit experiment, designed to probe the mysterious interplay between measurement, information, and the fundamental nature of reality in quantum mechanics. In this variation, electrons are fired individually toward a double-slit apparatus equipped with detectors that record which slit each electron passes through, thereby acquiring which-path information that typically destroys the interference pattern due to wavefunction collapse. However, before the electrons reach the detection screen, a quantum eraser mechanism is employed to "erase" the which-path information, effectively restoring the conditions necessary for interference. Classical physics dictates that once information about a system is obtained, the outcome is irrevocably fixed. Yet, the observed results defy this expectation: the interference pattern characteristic of wave-like behavior re-emerges when the which-path information is erased, even after the electrons have passed through the slits. This experiment highlights the non-classical relationship between knowledge and physical reality, illustrating how the mere potential to know certain information can influence the behavior of quantum systems. It underscores fundamental concepts such as quantum superposition, entanglement, and the observer effect, challenging our conventional notions of causality and time. By demonstrating that actions taken after a particle has entered the detection apparatus can alter the pattern it produces, the Quantum Eraser Experiment with electrons exemplifies the inherent "weirdness" of quantum mechanics and continues to intrigue and inspire deeper inquiries into the quantum realm.

  • Experimental Setup
    • Which-Path Information Recorded: A detector marks which slit each electron passes through, but this information is not immediately observed.
    • Quantum Erasure: Before the electrons reach the detection screen, the which-path information is "erased" using a quantum eraser setup.
    • Electron Source: Individual electrons emitted toward the slits.
    • Detection Screen: Records electron impacts as usual.
  • Expected Result
    • Without Erasure: If which-path information is recorded, interference should not occur.
    • With Erasure: Erasing the which-path information should restore the interference pattern, even though the electrons have already passed through the slits.
  • Observed Result
    • Restored Interference Pattern: When the which-path information is erased, the interference fringes reappear on the detection screen.
    • Dependence on Information: The pattern depends on whether the which-path information is available, not on the physical setup alone.
  • Explanation
    • Information's Role in Quantum Mechanics: The availability of which-path information affects the system's behavior.
    • Delayed Choice: The decision to erase the information can be made after the electrons have passed through the slits, suggesting non-classical temporal relationships.
    • Non-Locality and Entanglement: Quantum erasure demonstrates the non-local and non-classical correlations inherent in quantum systems.

Case 7 : Variation with Electron Beam Intensity

The "Variation with Electron Beam Intensity" in the double-slit experiment explores how the density of electrons affects the manifestation of quantum interference patterns, providing deeper insight into the wave-particle duality of matter. In this setup, the intensity of the electron beam is systematically altered—from a high-intensity stream where electrons are emitted in rapid succession to a low-intensity beam where electrons are emitted one at a time with significant intervals between them. Classical physics would predict that changing the beam intensity should not fundamentally affect the interference pattern, as electrons are considered independent particles that do not influence each other's trajectories. However, quantum mechanics reveals a more nuanced reality: at high intensities, the increased likelihood of electron-electron interactions can lead to decoherence, blurring or diminishing the interference pattern on the detection screen. Conversely, at low intensities, where electrons traverse the apparatus in isolation, a clear and well-defined interference pattern emerges over time, illustrating that individual electrons interfere with themselves rather than with other electrons. This variation underscores the delicate interplay between particle interactions and quantum coherence, highlighting how quantum effects can be influenced by experimental conditions. It challenges classical intuitions about particle behavior and emphasizes the inherent "weirdness" of the quantum world, reinforcing the necessity of quantum mechanical explanations for phenomena at microscopic scales.

  • Experimental Setup
    • High-Intensity Electron Beam: Electron source emits a dense stream of electrons, increasing the likelihood of electron-electron interactions.
    • Low-Intensity Electron Beam: Electrons are emitted at a much lower rate to minimize interactions.
    • Slit Structure and Detection Screen: Remain constant.
  • Expected Result
    • Classical Prediction: Higher intensity might lead to different patterns due to interactions; lower intensity should reduce these effects.
    • Quantum Prediction: Interference patterns should be observable regardless of beam intensity if electrons do not interact.
  • Observed Result
    • High Intensity: The interference pattern may become less clear due to electron-electron repulsion causing slight deviations in trajectories.
    • Low Intensity: A clear interference pattern emerges, confirming that individual electrons interfere with themselves, not with other electrons.
  • Explanation
    • Coulomb Repulsion: At high densities, electrons can repel each other, affecting their paths and blurring the interference pattern.
    • Self-Interference: At low intensities, electrons act independently, and their wavefunctions interfere without external disturbances.
    • Importance of Isolation: Minimizing interactions is crucial for observing pure quantum effects.

Case 8 : Modifying Slit Width and Separation

The "Modifying Slit Width and Separation" variation of the double-slit experiment investigates how changes in the physical dimensions of the slits influence the interference patterns produced by particles such as electrons or photons. In this setup, researchers systematically adjust the widths of the slits and the distance between them to observe the resulting effects on the interference fringes observed on the detection screen. Classical physics would predict that altering these dimensions might proportionally affect the distribution of particles, but it would not fundamentally change their behavior; particles would still travel in straight lines, and any variations in the pattern would be attributed to simple geometric considerations. However, quantum mechanics reveals a more intricate reality: the characteristics of the interference pattern—such as fringe spacing, intensity, and visibility—are highly sensitive to the slit dimensions due to the wave-like nature of particles at the quantum scale. By modifying the slit width and separation, the experiment demonstrates how the wavefunctions associated with particles interfere constructively and destructively in different ways, leading to observable changes in the pattern. This variation underscores the principles of wave-particle duality and superposition, highlighting how even small alterations in experimental parameters can lead to significant and sometimes non-intuitive outcomes. It offers deeper insights into the fundamental nature of quantum phenomena and reinforces the inherent "weirdness" of the quantum world, where particles do not always behave in ways that align with classical expectations

  • Experimental Setup
    • Variable Slit Widths (a): Changing the width of the slits to see how it affects diffraction and interference.
    • Variable Slit Separation (d): Adjusting the distance between the slits.
    • Electron Source and Detection Screen: Standard setup.
  • Expected Result
    • Classical Prediction: Variations in slit dimensions should proportionally affect the patterns, but classical particles would still form two impact regions.
    • Quantum Prediction: The interference fringe spacing and intensity distribution should change according to the slit dimensions.
  • Observed Result
    • Altered Interference Patterns: Changes in slit width and separation lead to predictable modifications in the interference fringes' spacing and visibility.
    • Consistent with Wave Equations: The patterns match calculations based on wave interference principles (e.g., the double-slit interference formula).
  • Explanation
    • Wave Mechanics: The position of interference fringes is given by the equation:
      • d × sin(θ) = m × λ
      • where
        • d  is slit separation,
        • θ is the angle of the fringe from the central maximum,
        • m  is the order of the fringe, and
        • λ is the electron's de Broglie wavelength.
    • Demonstration of Wave Properties: The dependence of the interference pattern on slit dimensions reinforces the wave-like behavior of electrons.

How small it should be ?

How small the particle should be to show this kind of wave like behavior ?

That's question that delves into the heart of quantum mechanics!  It's not so much about a specific size limit, but rather about the de Broglie wavelength of the particle.

Some basic/fundamental idea behind this are :

  • Everything has a wave nature: According to quantum mechanics, every object, regardless of its size, has a wave associated with it. This is called the de Broglie wave.  
  • Wavelength and momentum: The wavelength of this wave is inversely proportional to the object's momentum (mass times velocity). This means that heavier objects and faster-moving objects have shorter wavelengths.  
  • Observing wave behavior: For us to observe the wave-like behavior of an object, its de Broglie wavelength needs to be comparable to the size of the slits or obstacles it's interacting with.

So a broad answer to the questions is :

  • Small particles, big wavelengths: Tiny particles like electrons, protons, and neutrons have relatively large de Broglie wavelengths, making it easier to see their wave-like behavior in experiments like the double-slit.  
  • Large objects, tiny wavelengths: Macroscopic objects like baseballs, cars, and humans have incredibly tiny de Broglie wavelengths.This is why we don't see them exhibiting wave-like behavior in our everyday lives. Their wavelengths are so small that they don't interact with the world in a way that produces noticeable interference or diffraction effects.  

Now let's think of this in a little bit formal (meaning boring :) way if you are interested :

How Small Must a Particle Be to Exhibit Wave-like Behavior?

The wave-like behavior of particles, such as that seen in the double-slit experiment, depends on the wavelength associated with the particle, which is given by the de Broglie wavelength. This wavelength is inversely proportional to the particle's momentum, and it plays a critical role in determining whether wave-like behavior (such as interference) can be observed.

De Broglie Wavelength:

The de Broglie wavelength λ of a particle is given by:

λ = h / p

Where:

  • λ = de Broglie wavelength of the particle.
  • h = Planck's constant ( 6.626 × 10-34 Js ).
  • p = momentum of the particle, calculated as p = mv, where m is the particle’s mass and v is its velocity.

Key Factors for Wave-like Behavior:

  1. Wavelength Relative to Slit Size:
    • To observe interference effects like those in the double-slit experiment, the particle’s wavelength should be comparable to or larger than the slit width.
    • If the de Broglie wavelength is too small relative to the slit size, the wave-like nature of the particle will be overshadowed by its particle-like behavior, and the interference pattern will not be visible.
  2. Mass and Speed of the Particle:
    • For very large particles like baseballs, the de Broglie wavelength is extremely tiny because their momentum is large (due to their significant mass and velocity).
    • For very small particles like electrons or photons, the de Broglie wavelength can be large enough to observe interference patterns.
    • In practice, particles with masses up to that of molecules have been shown to exhibit wave-like behavior in carefully controlled experiments.

Practical Examples of Wave-like Behavior:

  • Electrons:
    • Electrons have a small mass ( 9.11 × 10-31 kg ). When they are accelerated to typical velocities in laboratory experiments, their de Broglie wavelength is on the order of nanometers (10-9 meters).
    • This is comparable to the spacing in double-slit experiments, so electrons exhibit clear interference patterns.
  • Neutrons:
    • Neutrons, which are more massive than electrons ( 1.675 × 10-27 kg ), have a shorter de Broglie wavelength at similar speeds but still can display interference patterns under certain conditions.
    • Interference has been demonstrated with neutrons using neutron interferometry.
  • Large Molecules:
    • Wave-like behavior has even been observed with larger particles like fullerenes (buckyballs, C60), which are molecules with around 60 carbon atoms.
    • For example, in experiments where these molecules are cooled and slowed down to low speeds, their de Broglie wavelength becomes large enough to produce observable interference patterns.
  • Atoms and Small Molecules:
    • Atoms and small molecules (e.g., He, H2) have also been used in double-slit-like experiments, demonstrating that their wave-like nature can be detected if they are sufficiently slow and their environment is isolated from external disturbances.

When Does Wave-like Behavior Disappear?

  • Macroscopic Objects: For everyday objects, like baseballs, the de Broglie wavelength becomes incredibly small (on the order of 10-30 meters or smaller), far too small to observe any wave-like behavior. Their particle-like nature dominates.
  • Quantum Coherence and Environment: For larger particles to show wave-like behavior, they must be isolated from their environment to prevent interactions that lead to decoherence. Interactions with the environment (like air molecules) can collapse the wave-like nature into a definite particle-like state, making interference patterns disappear.

Practical Threshold:

There is no strict cutoff for when a particle stops behaving like a wave and starts behaving like a particle; instead, it’s a matter of scale and context. Generally, for wave-like behavior to be observable:

  • The particle must have a small enough mass or low enough momentum so that its de Broglie wavelength is comparable to the experimental setup (e.g., slit size).
  • The environment must be controlled to minimize decoherence, especially for larger particles.

In summary, quantum interference is primarily observable for electrons, neutrons, atoms, and small molecules, with successful demonstrations in molecules containing up to thousands of atoms. Beyond that, achieving and maintaining the conditions required to observe such wave-like behavior becomes increasingly challenging due to the influence of decoherence and the decreasing de Broglie wavelength.

Why Complex Amplitudes Matter: Unraveling Quantum Behavior in the Double-Slit Experiment

Actually the main reason why I decided to write a note on double slit experiment is to find answers to this question. In short, I wanted to understand the meaning of the following state function in more tangible way from double slit experiment .

My main questions are

  • α and β are complex numbers
  • why these numbers should be expressed as complex number ?
  • How to interpret the meaning of α and β (not α2 and β2)

The double-slit experiment provides a tangible way to understand the quantum state function, Ψ = α |0> + β |1>. In this equation, α and β are complex numbers representing the probability amplitudes associated with different quantum states. Specifically, |0⟩ might represent the particle going through slit 0, while |1⟩ represents the particle going through slit 1.

Why Are α and β Complex Numbers?

  • Not Directly Probabilities:
    • α and β themselves do not directly represent probabilities. Instead, their squared magnitudes—|α|2 and |β|2—determine the probabilities of finding the particle in state |0⟩ (e.g., passing through slit 0) or |1⟩ (e.g., passing through slit 1).
    • The values of |α|2 and |β|2 must sum to 1, ensuring that the total probability of the quantum state adds up to 100%.
  • Role of Amplitude and Phase:
    • The reason α and β are expressed as complex numbers is due to the need to capture both amplitude (which contributes to the probability) and phase (which affects interference). Each complex number can be written in the form α = |α| eiφα, where |α| is the magnitude and φα is the phase.
    • The phase component is essential for understanding interference effects. In the double-slit experiment, the phase difference between α and β determines how the waves associated with each path (slit 0 or slit 1) interfere when they overlap on the detection screen.

Interpreting the Meaning of α and β in the Double-Slit Experiment

  • Combined Effect of Amplitude and Phase:
    • While |α|2 and |β|2 provide the probabilities of different outcomes, α and β as complex numbers contain additional information about how these probabilities interact through their phases.
    • The interference pattern in the double-slit experiment arises from the way the phases of α and β interact. The probability of detecting the particle at a specific point on the detection screen is influenced by the combined phase relationship between the waves through slit 0 and slit 1.
  • How Phase Influences Interference:
    • Constructive interference (bright fringes) occurs when the phase difference between α and β leads to their wave amplitudes aligning. Destructive interference (dark fringes) occurs when the phase difference causes the waves to cancel each other out.
    • The term 2 |α| |β| cos(φα - φβ) in the probability expression describes this phase-dependent interference, showing how the relative phases of α and β shape the resulting pattern.

Summary: Why This Matters for the Double-Slit Experiment

Understanding of α and β is key to appreciating the double-slit experiment's insights into quantum mechanics:

  • α and β are not probabilities themselves; rather, they are complex probability amplitudes whose squared magnitudes determine the likelihood of certain outcomes.
  • The complex nature of α and β captures both the magnitude (which affects probabilities) and the phase (which affects interference). This allows quantum mechanics to accurately describe wave-like behaviors such as interference.
  • The phase difference between α and β is crucial for understanding the formation of interference patterns in the double-slit experiment, illustrating how quantum superposition and wave-particle duality give rise to results that defy classical expectations.

Thus, α and β as complex numbers allow us to describe the intricate interplay of quantum states, making them essential for understanding the deeper mechanics of phenomena like the double-slit experiment. This is why the use of complex numbers is fundamental in quantum mechanics—enabling a richer description of reality that goes beyond the capabilities of classical physics.

Interference Unveiled: The Practical Impact of Complex Phases in Quantum Probability

Even reading a lot of articles and watching many videos, the term 'interference' didn't sound clear to me. I hope this section would help you get clearer understanding on the practical meaning of 'interference' , i.e, the phase differences between the two states. If you understand this clearly, you would have clearer understanding on the nature of complex numbers in the quantum state function.

In the context of the double-slit experiment and quantum mechanics, interference refers to how the quantum states associated with different paths—like |0> and |1> in a superposition—combine to influence the probability of a particular outcome when measured. It is a result of the wave-like nature of quantum states, where the phases of these states interact and affect the likelihood of finding a particle in a certain position on the detection screen.

Practical Meaning of Interference

  • Interference Patterns on the Screen:
    • In a double-slit experiment, when a quantum particle like an electron or photon passes through the slits, its wavefunction splits into components that correspond to the paths through each slit—|0⟩ (through slit 0) and |1⟩ (through slit 1).
    • These components carry complex phases, which determine how the probability amplitudes (described by α and β) interact when they recombine on the detection screen.
    • The result is an interference pattern—a distribution of bright and dark fringes on the detection screen—where the probability of detecting the particle varies across different points.
  • Constructive and Destructive Interference:
    • Constructive Interference: Occurs when the phases of the probability amplitudes α and β align in such a way that their waves reinforce each other. This increases the probability of detecting the particle at specific positions (bright fringes).
    • Destructive Interference: Occurs when the phases differ by a value such that their waves cancel each other out. This decreases or even eliminates the probability of detecting the particle at those points (dark fringes).

Phase Interaction Between |0> and |1>

  • Influence of Phase Differences:
    • The phases associated with |0> and |1> do influence each other when the wavefunctions overlap. The phase of the state |0⟩ (associated with the path through slit 0) can constructively or destructively interfere with the phase of the state |1⟩ (associated with the path through slit 1).
    • This means that the phase of the component α |0⟩ (where α = |α| eiφα) can directly affect the probability of detecting the particle at locations where the component β |1⟩ (where β = |β| eiφβ) also contributes.
  • Practical Consequence:
    • If the phase difference between α and β is such that the contributions from |0> and |1> align positively, the probability of finding the particle at those positions increases (constructive interference).
    • Conversely, if the phase difference is such that they are out of phase, the probability decreases (destructive interference).

Key Takeaway:

  • Interference is Not About a Direct Influence on the Probability of a State:
    • It’s not that the phase of state |0> directly changes the probability of finding the particle in state |1> or vice versa in the classical sense.
    • Instead, it’s about how the phases of the superposed states  |0> and |1> combine when calculating the overall probability of detecting the particle in specific positions on the screen. The wavefunctions interact through their phases, altering the overall probability distribution rather than influencing each state individually.
  • Interference Reflects Quantum Superposition:
    • The interference pattern seen in the double-slit experiment reflects the superposition of the quantum states |0> and |1> . It is the manifestation of how the quantum possibilities "interfere" with each other before measurement collapses the wavefunction into a definite outcome.
    • Thus, the phases of α and β are crucial in determining where constructive or destructive interference occurs, which in turn shapes the pattern of bright and dark fringes on the detection screen.

In summary, interference in this context describes how the combined wavefunctions associated with passing through each slit affect the final probability distribution due to the interplay of their complex phases. It’s this phase-based interaction that leads to

Reference

YouTube