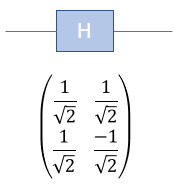
Hadamard Gate is one of the most famous Gate in Quantum Computing. It takes a state of a Qbit and produce the equal mixture of |0> and |1>.  

The Hadamard gate (H gate) is a fundamental single-qubit quantum gate that plays a crucial role in creating superposition states and transforming the basis of a qubit. It is a key component in many quantum algorithms and serves as a building block for more complex quantum operations.

Think of the Hadamard gate as a tool that turns a definite answer (yes or no) into a maybe, and then allows the quantum computer to explore the consequences of both possibilities simultaneously. This ability to explore multiple paths at once is what gives quantum computers their potential advantage over classical computers.

How H Gate operates ?

Hadamard Gate is represented as follows.   

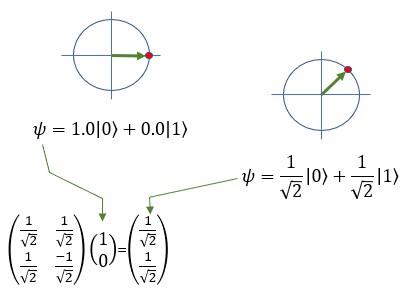
As I said, it would always be confusing if you try to understand the quamtum operation verbally. Eventually you would need to turn to mathematics to have clearer and long lasting understanding.

First, let's take an example where a Qbit with the probability of 100% for |0> and 0% of |1> go through H(Hadamard) gate. This procedure results in a Qbit with the probability of 50% for |0> and 50% for |1>. It can be represented mathematically as shown below. (If you are not familiar with mathematical representation, try reading Qbit page)   

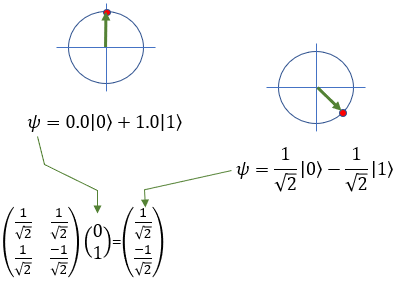
Now, let's take another example where a Qbit with the probability of 0% for |0> and 100% of |1> go through H(Hadamard) gate. This procedure results in a Qbit with the probability of 50% for |0> and 50% for |1>. It can be represented mathematically as shown below. (If you are not familiar with mathematical representation, try reading Qbit page)   

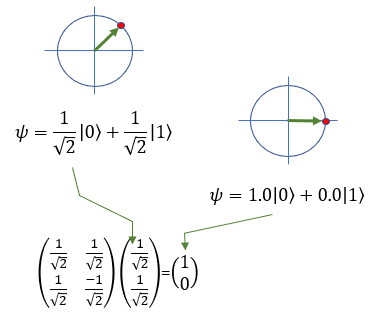
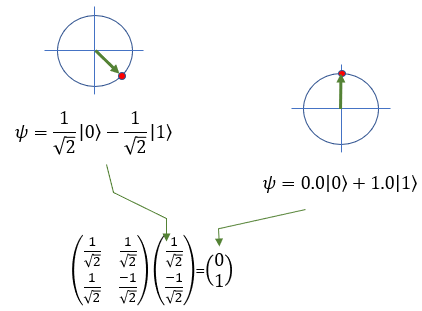
How about applying H gate to the superpositioned state. Following is an example. Application of H Gate to the superpositioned states of |0> gives the original state, meaning |0> - [H] - [H] gives |0>.

Let's take a look at another example. Application of H Gate to the superpositioned states of |1> gives the original state, meaning |1> - [H] - [H] gives |1>.

What does it do ?

The Hadamard gate performs two main functions:

• Creates Superposition: When applied to a qubit in a definite state (either |0⟩ or |1⟩), it transforms the qubit into a superposition state, where it has an equal probability of being measured as |0⟩ or |1⟩. This is like putting the qubit in a balanced state of both possibilities.
• Changes Basis: It changes the basis of a qubit from the computational basis (|0⟩ and |1⟩) to the Hadamard basis (|+⟩ and |-⟩). This is akin to switching the perspective from which you view the qubit's information.

Why is it important?

The Hadamard gate is a cornerstone of quantum computing because:

• Superposition is key: Superposition is a fundamental aspect of quantum mechanics that allows quantum computers to explore multiple solutions simultaneously, potentially leading to faster computations.
• Algorithms rely on it: Many quantum algorithms, like Grover's search algorithm and Deutsch-Jozsa algorithm, utilize the Hadamard gate to create and manipulate superposition states.
• Quantum parallelism: By creating superposition states, the Hadamard gate enables quantum parallelism, where a quantum computer can perform calculations on all possible inputs at once.