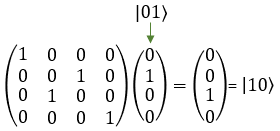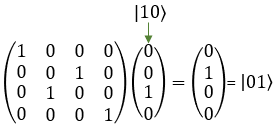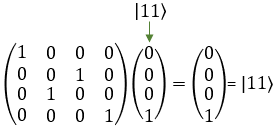|
|
||
|
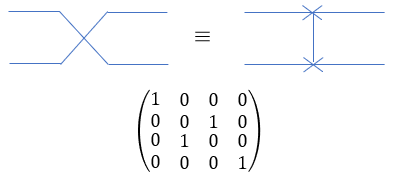
The primary function of the SWAP gate is to "swap" the states of two qubits. Imagine you have two cups, one filled with water (representing a qubit with a particular state) and the other filled with orange juice (representing another qubit with a different state). The SWAP gate acts like a process that allows you to exchange the contents of the two cups so that the water ends up in the cup that initially contained orange juice, and the orange juice ends up in the cup that initially contained water. In this process, the states of the two qubits (cups) are effectively swapped. To perform this swapping operation, the SWAP gate requires two qubits as inputs. After applying the SWAP gate, the state of the first qubit becomes the state of the second qubit, and vice versa. The SWAP gate is reversible, meaning you can apply it again to restore the original states of the qubits. The SWAP gate plays an essential role in quantum computing when you need to rearrange the order of qubits in a quantum circuit or when you want to move information from one qubit to another. In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 4x1 vector (representing 2 qubit) and swap the elements within the vector.
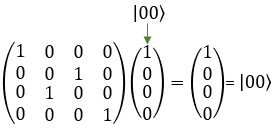
If I you plug in the state vector for |00> , |01>, |10> and |11> into SWAP gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate SWAP matrix.
|
||