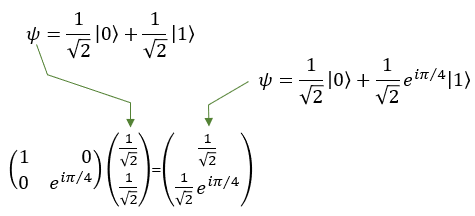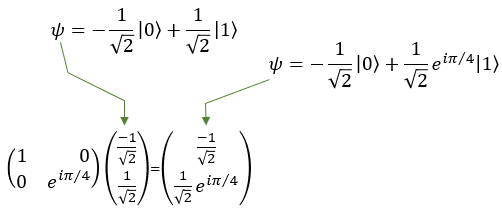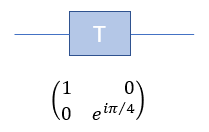
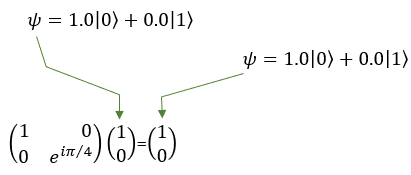
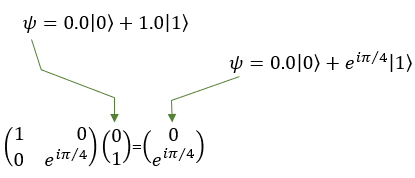
Quamtum Gate - T

The T gate is also known as the pi/4 gate working on a single qubit.

The T gate is a phase gate that applies a phase shift to the qubit's state, specifically to the |1> state, while leaving the |0> state unchanged. In layman's terms, the T gate slightly alters the "phase" of the qubit's state, which is a critical aspect of quantum mechanics.

The T gate rotates the qubit state around the Z-axis of the Bloch sphere by π/4 (pi/4) or 45 degrees. When the T gate is applied to the basis states, the result is:

T|0> = |0>

T|1> = e^(iπ/4)|1>

Here, e^(iπ/4) represents the phase shift applied to the |1> state

Since qubits can exist in superpositions, the T gate can also transform states that are combinations of |0> and |1>. For example, consider a qubit in the following superposition state:

|ψ> = a|0> + b|1>, where a and b are complex numbers representing the amplitudes of the qubit states.

When the T gate is applied to this qubit, the result will be:

T|ψ> = a|0> + e^(iπ/4)b|1>

As you can see, the T gate has applied a phase shift to the amplitude of the |1> state, while the amplitude of the |0> state remains the same.

In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 2x1 vector (representing 1 qubit) and swap the elements within the vector.

If I you plug in the state vector for |0> and |1> into T gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate T matrix.