Quantum Computing  

 

 

 

Quantum State Function

In the realm of quantum computing, we encounter the fascinating concept of the Quantum State Function. Think of it like this: you already know how in classical computing we use math to represent a bit as either 0 or 1. That's pretty straightforward, right? Well, in the quantum world, a qubit isn't so easily pinned down. Instead of being definitively 0 or 1, it exists in this hazy, uncertain state—a blend of both 0 and 1 simultaneously. This 'blurry mixture' of multiple states is what we capture mathematically using a special form of function. This special form of function to represent a specific state of a quantum bit is called Quantum State Function. It's a powerful tool that helps us understand and work with the unique behavior of qubits.

In more formal words

Now let's talk about quantum state function in a little bit formal way.

In quantum computing, a quantum state function describes the state of a quantum system, much like a variable or data structure in traditional programming, but with some unique properties. For a single quantum bit (qubit), this state function is typically written as:

|ψ〉 = α|0〉 + β|1〉

Here’s a breakdown that fits a software engineering mindset:

  • Qubit: The fundamental unit of quantum information, like a bit in classical computing. It can be in the state |0〉, |1〉, or any combination (superposition) of both.
  • Superposition: Unlike a classical bit that is either 0 or 1, a qubit can be in a state that is simultaneously a mix of |0〉 and |1〉. The coefficients α (alpha) and β (beta) in the state function are complex numbers that define how much of |0〉 and |1〉 are in this mix.
  • Probability Interpretation: When we measure the qubit, it "collapses" to either |0〉 or |1〉, with probabilities defined by the squared magnitudes of α and β. Specifically:
    • |α|2 is the probability that the qubit will collapse to |0〉.
    • |β|2 is the probability that it will collapse to |1〉.
    • These probabilities must sum to 1 (|α|2 + |β|2 = 1).
  • Phase: The fact that α and β are complex numbers means that the state of a qubit also has a phase component. The relative phase between α and β influences the outcomes when qubits are entangled or interfere with each other. This phase information is crucial in many quantum algorithms, enabling them to perform tasks like interference-based computations.

In programming terms, think of |ψ〉 as a vector or a list containing two complex numbers (α and β), representing how the qubit behaves when manipulated and measured. Understanding and manipulating this quantum state is key to performing computations on a quantum computer.

Understanding the canonical definition of a quantum state function as described above is important and it provides the mathematical foundation for describing how qubits behave. However, the abstract nature of concepts like superposition, phase, and interference can be challenging to grasp through equations alone. This is why illustrative examples, like specific cases with defined values for α and β, are essential. These examples translate complex mathematical ideas into more intuitive visualizations, allowing us to see how phase affects interference patterns, and how probabilities change based on the qubit's state. By bridging the gap between theory and intuition, such examples make the principles of quantum mechanics more accessible to those with backgrounds in programming and engineering, offering deeper insights into how quantum algorithms work in practice.

Example 1: Pure State |0〉

    Quantum State:

      |ψ〉 = 1|0〉 + 0|1〉

      , indicating α = 1, β = 0

    Interpretation:

    • This state means that the qubit is definitely in the state |0〉.
    • |α|2 = 1, which means a 100% probability of measuring the qubit as |0〉.
    • |β|2 = 0, which means a 0% probability of measuring the qubit as |1〉.

    This corresponds to a classical bit being 0.

 

Example 2: Pure State |1〉

    Quantum State:

      |ψ〉 = 0|0〉 + 1|1〉

      , indicating α = 0, β = 1

    Interpretation:

    • This state means that the qubit is definitely in the state |1〉.
    • |α|2 = 0, which means a 0% probability of measuring the qubit as |0〉.
    • |β|2 = 1, which means a 100% probability of measuring the qubit as |1〉.

    This corresponds to a classical bit being 1.

 

Example 3: Superposition State

    Quantum State:

      |ψ〉 = √2/2|0〉 + √2/2|1〉

      , indicating α = √2/2, β = √2/2

    Interpretation:

    • This state is a balanced superposition of |0〉 and |1〉.
    • |α|2 = (√2/2)2 = 0.5, which means a 50% probability of measuring the qubit as |0〉.
    • |β|2 = (√2/2)2 = 0.5, which means a 50% probability of measuring the qubit as |1〉.

    This is one of the most basic examples of a qubit in superposition, where it has an equal chance of collapsing to |0〉 or |1〉 when measured.

 

Example 4: Unequal Superposition State

    Quantum State:

      |ψ〉 = 1/3|0〉 + 2√2/3|1〉

      , indicating α = 1/3, β = 2√2/3

    Interpretation:

    • |α|2 = (1/3)2 = 1/9 ≈ 0.11, which means about an 11% probability of measuring the qubit as |0〉.
    • |β|2 = (2√2/3)2 = 8/9 ≈ 0.89, which means about an 89% probability of measuring the qubit as |1〉.

    In this state, the qubit is more likely to be measured as |1〉, but there is still a small chance it will collapse to |0〉.

 

Example 5: State with a Phase

    Quantum State:

      |ψ〉 = 1/√2|0〉 + i/√2|1〉

      α = 1/√2, β = i/√2

    Interpretation:

    • |α|2 = (1/√2)2 = 0.5, which means a 50% probability of measuring the qubit as |0〉.
    • |β|2 = (i/√2)2 = 0.5, which means a 50% probability of measuring the qubit as |1〉.
    • The presence of i in β indicates that this state has a relative phase of 90 degrees (π/2 radians) between |0〉 and |1〉.

    This state still has equal probabilities for |0〉 and |1〉, but the phase difference can influence how this qubit interacts with others.

 

Example 6: State with a 45-Degree Phase

    Quantum State:

      |ψ〉 = √2/2|0〉 + √2/2eiπ/4|1〉

      α = √2/2, β = √2/2eiπ/4

    Interpretation:

    • |α|2 = (√2/2)2 = 0.5, meaning a 50% probability of measuring the qubit as |0〉.
    • |β|2 = (√2/2)2 = 0.5, meaning a 50% probability of measuring the qubit as |1〉.
    • Phase Difference: The phase factor eiπ/4 represents a 45-degree phase shift. This phase does not change the probabilities of measuring |0〉 or |1〉 but affects how the qubit interacts with other qubits, especially during operations like interference and entanglement.

 

Example 7: State with a 180-Degree Phase (π Radians)

    Quantum State:

      |ψ〉 = √3/2|0〉 + √3/2eiπ|1〉

      α = √3/2, β = √3/2eiπ

    Interpretation:

    • |α|2 = (√3/2)2 = 0.75, meaning a 75% probability of measuring the qubit as |0〉.
    • |β|2 = (√3/2)2 = 0.75, meaning a 75% probability of measuring the qubit as |1〉.
    • Phase Difference: The phase factor eiπ = -1 represents a 180-degree shift. This means that |1〉 is multiplied by -1, which can lead to destructive interference when combined with other qubits, altering the result of certain quantum operations.

 

Example 8: State with a 90-Degree Phase (π/2 Radians)

    Quantum State:

      |ψ〉 = 1/2|0〉 + i/√2|1〉

      α = 1/2, β = i/√2

    Interpretation:

    • |α|2 = (1/2)2 = 0.25, meaning a 25% probability of measuring the qubit as |0〉.
    • |β|2 = (i/√2)2 = 0.5, meaning a 50% probability of measuring the qubit as |1〉.
    • Phase Difference: The imaginary unit i in β corresponds to a 90-degree phase shift between |0〉 and |1〉. This phase difference can result in constructive or destructive interference patterns when this qubit interacts with others.

 

Example 9: General Complex Coefficients

    Quantum State:

      |ψ〉 = √2/3|0〉 + √2/3ei2π/3|1〉

      α = √2/3, β = √2/3ei2π/3

    Interpretation:

    • |α|2 = (√2/3)2 = 0.22, meaning about a 22% probability of measuring the qubit as |0〉.
    • |β|2 = (√2/3 ei2π/3)2 = 0.22, meaning about a 22% probability of measuring the qubit as |1〉.
    • Phase Difference: The phase factor ei2π/3 represents a 120-degree phase shift. This affects the way the qubit interferes with other qubits in a quantum system, which can be particularly important in quantum gates that rely on phase differences.

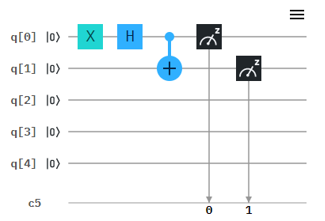
Why bother to understand Quantum State Function ?

Imagine you're trying to understand a quantum program. You see a sequence of quantum operations (gates), like a series of instructions. But here's the catch: these instructions are written in a language that directly manipulates the quantum state function.

Each gate is like a tiny machine that transforms the state function of a qubit. It might flip the probabilities, mix them in new ways, or even create entanglement with other qubits. Without understanding what the state function represents, you're essentially looking at these instructions with a blindfold on.

You won't grasp how each gate changes the qubit's state, how different gates combine to achieve a specific outcome, or ultimately, how the entire algorithm works its magic. It's like trying to decipher a coded message without the key.

So, understanding the state function is like having the Rosetta Stone for quantum programming. It allows you to decode the instructions, understand the mechanisms at play, and truly grasp the essence of quantum algorithms."

This approach emphasizes the direct link between the state function and quantum operations, making it clear why understanding the former is crucial for comprehending the latter.

Let's take a look into a simple quantum circuit and see how we can apply the quantum state function. Let's suppose we have a circuit as shown below.

How do you analyze this circuit (I assume that we already understand the operation/mechanism of each Gate used here : X, H, CNOT gate).

    1. Starting Point:

      Both qubits begin in the state |0⟩. So, our initial state function is:

      |ψ> = |00>

      // this is a state function of two bit quantum state |ψ⟩ = 1|00⟩ + 0|01⟩ + 0|10⟩ + 0|11⟩

    2. Flipping q[0]:

      We apply an X gate to q[0], which flips its state to |1⟩:

      |ψ> = X|00> = |10>

      // this is a state function of two bit quantum state |ψ⟩ = 0|00⟩ + 0|01⟩ + 1|10⟩ + 0|11⟩

    3. Creating Superposition:

      Now, we use a Hadamard (H) gate on q[0]. This puts q[0] into a superposition, a mix of |0⟩ and |1⟩:

      |ψ> = H|10> = (|0> + |1>)/√2 ⊗ |0> = (|00> + |10>)/√2

      // this is a state function of two bit quantum state |ψ⟩ = √2 |00⟩ + 0|01⟩ + √2 |10⟩ + 0|11⟩

      See how the state function now shows q[0] as a combination of both states?

    4. Entangling the Qubits:

      Next, we apply a CNOT gate, with q[0] as the control and q[1] as the target. This entangles the two qubits:

      |ψ> = CNOT ((|00> + |10>)/√2) = (|00> + |11>)/√2

       // this is a state function of two bit quantum state |ψ⟩ = √2 |00⟩ + 0|01⟩ + 0 |10⟩ + √2|11⟩

      The state function now shows that the qubits are linked. If we measure q[0] as |0>, q[1] will also be |0>. If we measure q[0] as |1>, then q[1] will be |1>. They are connected!

NOTE : Why This Matters ?

Without understanding the state function, we wouldn't be able to:

  • Track the changes: See how each gate changes the state of the qubits.
  • Understand superposition: Grasp how the H gate creates this "both-at-once" state.
  • Appreciate entanglement: Recognize how the CNOT gate links the fates of the two qubits.

This simplified example shows how the state function acts like a magnifying glass, allowing us to see the inner workings of a quantum circuit and understand the effects of each operation

Simply put, the explanation for each of the steps shown above are all expressed as manipulation of state functions.

Reference

  •  

YouTube