|
Electronics |
||
|
Impedance
Impedance was one of very confusing concept (terminology) to me. Followings are the many questions that comes up in my mind when I was first learning the concept of impedance. Are same questions annoying you as well ? When I first learn about 'Resistance' in high school physics, it said " Resistance is a tendancy to make current flow difficult" and it has sound intuitive to me for long time. As usual, I just tried to convert into a plain language when I first heard of 'impedance'. But as soon as I tried to convert it into plain language, all the confusion start poping up and I would get more questions as I was trying to get deeper into the concept. I don't see much difference in terms of plain language between 'Resistance' and 'Impedance'. But if there is no difference, why we need a new terminology ? So... I would say "Resistance" and "Impendance" has very close relationship but not exactly same. Then what is the difference ? This is what I am going to talk in next section.
What is impedance ?
Now let's try to define 'Impdeance' in more formal way. If I am asked to define 'Impedence' in my own words, I would define "Impedance is any form of tendancy to CHANGE the current flow". I used the word 'CHANGE' in my definition, not "OPPOSE" or "MAKE DIFFICULT". Of course, "OPPOSE" or "MAKE DIFFICULT" can be a kind of "CHANGE" but does not explain all aspect of "CHANGE".
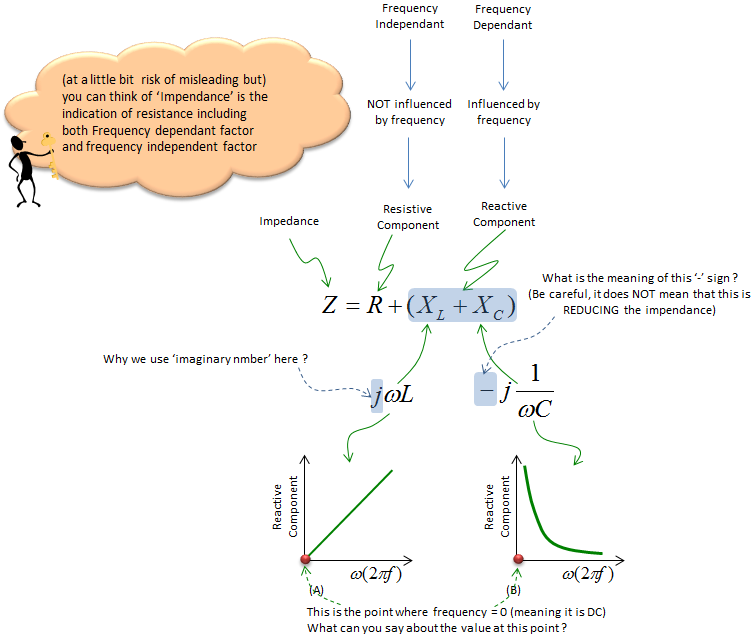
I understand you wouldn't much about the math -:), but sometimes it would be clearer/easier to understand a concept if the math is not too complicated. Let's try anyway. You will see the detailed meaning of this formula in following sections. Just try to get the big picture here. Also think about how you would answer the questions I put here.
At the point (A) where the frequency is 0, you see the value of Reactive Component is Zero (0). It mean that the reactive factor caused by an Inductor at frequency 0 becomes 0. Meaning the Inductor does not contribute anything to Impendence in DC circuit (you can say 'Frequency = 0' mean DC). Also you can say "L act like 'short' (or just a simple wire) in DC circuit".
At the point (B) where the frequency is Infinity, you see the value of Reactive Component is Infinity. It mean that the reactive factor caused by a Capacitor at frequency 0 becomes Infinitely large. you can say "C act like 'open' (or just a broken wire) in DC circuit".
Details of Each Impendence Component
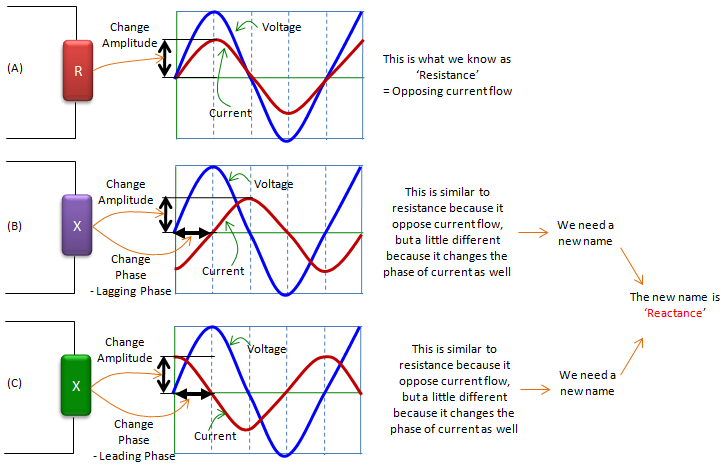
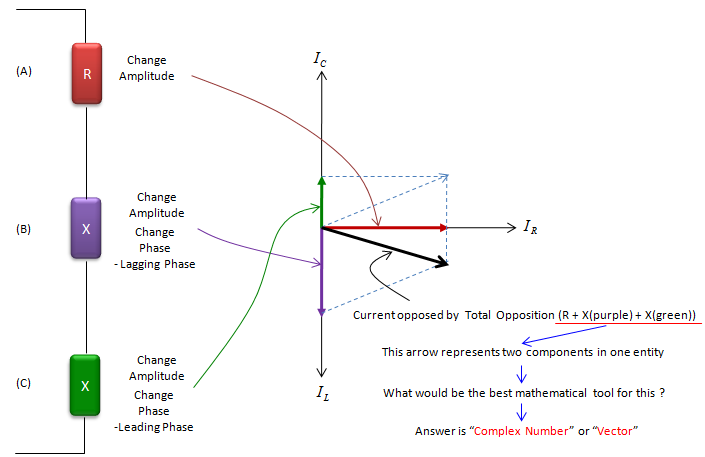
Let's look into following three illustration. We have three cases labeled (A), (B), (C) and each of the cases has single component labeled 'R', 'X', 'Y' respectively. Let's assume that we applied the same electrical source suppyplying AC voltage/current. (I will talk later about why I use AC (not DC) source here). On right side, you see the voltage and current graph measured across each of the component. Do each of the component appose current flow ? Yes. How do you know ? If it does not oppose current flow at all, the current flow should be infinately large.. but they are not infinately large here.. so we can say all of these component oppose(hinder) current flow. Then what is the difference among the case (A), (B), (C) ? The difference lies in the phase difference in current curve. In case (A), there is no phase difference between current and voltage curve. But in case (B), there is 90 degree phase difference between the voltage curve and current curve. (In (B), current curve is leading the voltage curve by 90 degree. In (C), current curve is lagging the voltage curve by 90 degree). The property (tendancy) to change the current flow as in case (A) is called 'Resistance' and The property (tendancy) to change the current flow as in case (B) or (C) is called 'Reactance'. The electrical device called 'Resistor' has property as in case (A). The electrical device called 'Inductor' has property as in case (B) and the electrical device called 'Resistor' has property as in case (C).
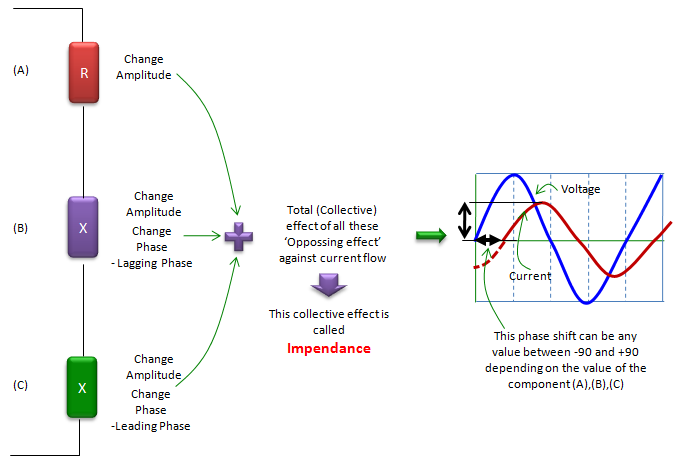
In real circuit (especially in AC circuit), there is not so many cases where you use only single type of component like type (A), (B), or (C). In most case, a circuit is made up of the combination of all of these types. And in reality, there is no devices which shows 100% of type (A) property and 0 % of type (B)/(C), and there is no device which shows 100% of type (B)/(C) property and 0 % of type (A). I would say every electrical device has at least a little bit of all of these three properties in it. So if we take a look at the current flow of overal circuit (or a block of circuit), we would see the combined effect of all the type (A), (B), (C). This combined property of type (A), (B), (C) is called 'Impedance' as illustrated below. As you see in this illustration, the impedance indicates two properties of current flow changes (current opposition property and phase change property) simultaneously.
Why we use a complex number for it ?
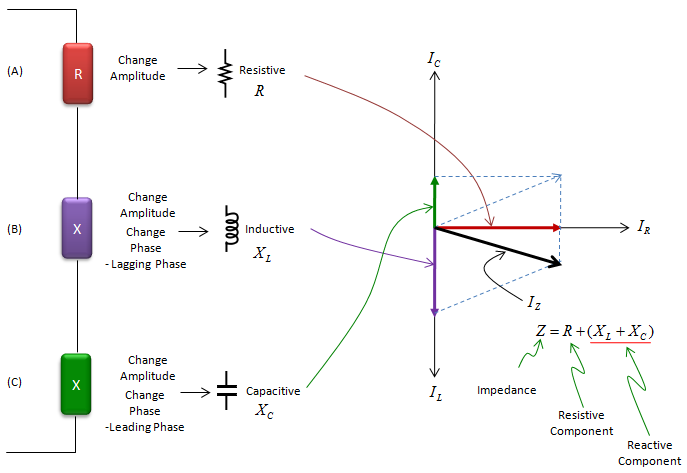
As I mentioned above, 'Impedence' is an indicator to show the combined properties of 'Resistance' and 'Reactance'. Then how can we represent this multiple properties in mathematical terms. You can think of a couple of possibility. One possibility is just to represent it as two separate numbers. Another possibility is to represent it in a vector with two element, and another possibility is to represent it as a complex number. What would be the best option ? It would be hard to mathematically prove which one is the best choice but it is most widely accepted to represent it as a complex number. The relationship between Registance/Reactance and the real/imaginary part of complex number is illustrated as below.
If you plug each electrical component (R,L,C) into the case shown above, you would understand how these electrical component properties can be represented in the complex number of Impedance. See the illustration below.
What is impedance matching ?
In most electrical circuit or a system, Energy is supplied from a source and go through multiple intermediate blocks and finally reaches the output of the circuit/system. And we usually tries to convey the energy from to source to the output with as little loss as possible. To minimize the energy loss while the energy propagate from one block to another block, one of the most important condition is that the impedance of a block and the impedance of next block should be same. Impedance Matching is a process (practice) of making the impendance of neighbouring blocks 'Matched'. (I used the term 'Matched', not 'Same'. You will see why later). Impedance matching is one of the most important things in most RF circuit design and implementation. It normally requires not only some theory behind it but also a lot of experience. Even more tricky thing is that a condition for impendance matching at a specific frequency may not work at another frequency. So it tends to be very difficult to find the best impedance matching condition for a component which has to work in wide frequency range (e.g, Wide band RF filters).
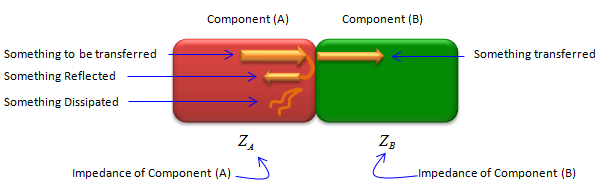
Putting it into an illustration, it can go as follows. If you put some energy into a component (labeled as (A)) and transfer it to a next block (labeled as (B)), the energy may split into three portions. Some portions would get transferred to (B) as we want, but some portion would bounce back to (A) and some other portion would get lost (dissipate as heat).
Our goal here is to maximize the portions of energy being transferred and minimize the engergy that is bounced back or lost. One way to do that is to adjust the impedance of each block so that they become 'matched'.
Then what does it mean by 'Matched' ? i.e, what is the condition for 'Matched Impedance' ? The answer can be summarized as below.
Recommended Video
|
||