|
|
||
|
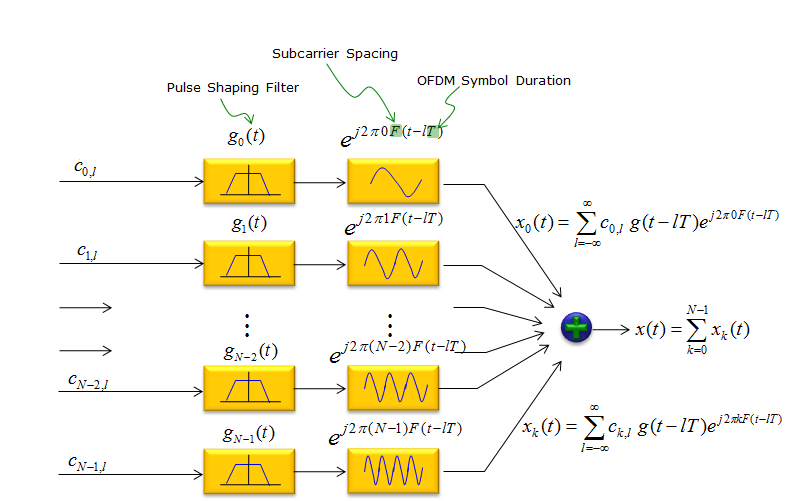
In this scheme, a filter is applied per sub carrier and can be modeled as shown below. Basic concept and characteristics of FBMC is well explained in the video 5G Waveform Comparison from Anritsu as stated below. In FBMC, Each of the individual sub-channel is filtered on its own. It uses the very narrow band filter with long time length. This gives us very good control of each filter bank. It gives a good control over emisson of each of the subcarriers. We have very good spectral efficieny and very good data rate but because we don't have cyclic prefix, it is a little difficult to process MIMO. It is not supporting very well for the large MIMO array technology. For those application with MIMO or short time/burst transmission, it is not so effective. The important thing is that each of the subcarrier goes through a filter called 'Pulse Shaping Filter'.
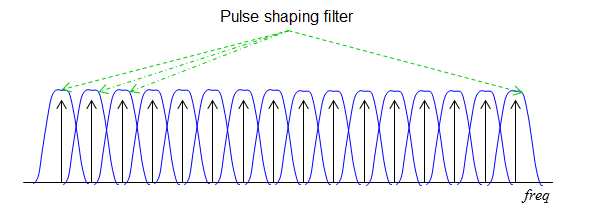
The process illustrated above can be represented in more intuitive way as shown below. As you see, each of sub channel goes through a bandpass filter.
The critical steps for FBMC is to implement filters for each sub channels and align the multiple filters into a filter bank. The way to build the filter bank is .. we design a basic form (template) of a filter called prototype filter. Once we finish the design of the prototype filter, the next step is simple. Just make a copy of the prototype filter and shift it to neighbouring sub channels step by step. (Following illustration is based on Ref [4])
Example 01 > --------------------------------------------------------------------------------------------------- Following is an example of generating FBMC signal. The generation part came from Michel TERRE's Matlab code (Refer to Ref [5] for original code and Copyright Info). I added plotting parts and I will describe on each of the steps. clear all; close all; clc; N=16;
% Prototype Filter (cf M. Bellanger, Phydyas project) H1=0.971960; H2=sqrt(2)/2; H3=0.235147; factech=1+2*(H1+H2+H3); hef(1:4*N)=0; for i=1:4*N-1 hef(1+i)=1-2*H1*cos(pi*i/(2*N))+2*H2*cos(pi*i/N)-2*H3*cos(pi*i*3/(2*N)); end hef=hef/factech;
% % Prototype filter impulse response h=hef;
% Initialization for transmission Frame=1; y=zeros(1,4*N+(Frame-1)*N/2);
s=zeros(N,Frame); for ntrame=1:Frame
% OQAM Modulator if rem(ntrame,2)==1 s(1:2:N,ntrame)=sign(randn(N/2,1)); s(2:2:N,ntrame)=j*sign(randn(N/2,1)); else s(1:2:N,ntrame)=j*sign(randn(N/2,1)); s(2:2:N,ntrame)=sign(randn(N/2,1)); end
x=ifft(s(:,ntrame));
% Duplication of the signal x4=[x.' x.' x.' x.'];
% We apply the filter on the duplicated signal signal=x4.*h; %signal=x4;
% Transmitted signal y(1+(ntrame-1)*N/2:(ntrame-1)*N/2+4*N)=y(1+(ntrame-1)*N/2:(ntrame-1)*N/2+4*N)+signal;
end
yfft = [zeros(1,length(y)/2) fft(y) zeros(1,length(y)/2)] yTx = ifft(yfft); yTxFreq = fft(yTx,8192); yTxFreqAbs = abs(yTxFreq); yTxFreqAbs = yTxFreqAbs/max(yTxFreqAbs); yTxFreqAbsPwr = 20*log(yTxFreqAbs);
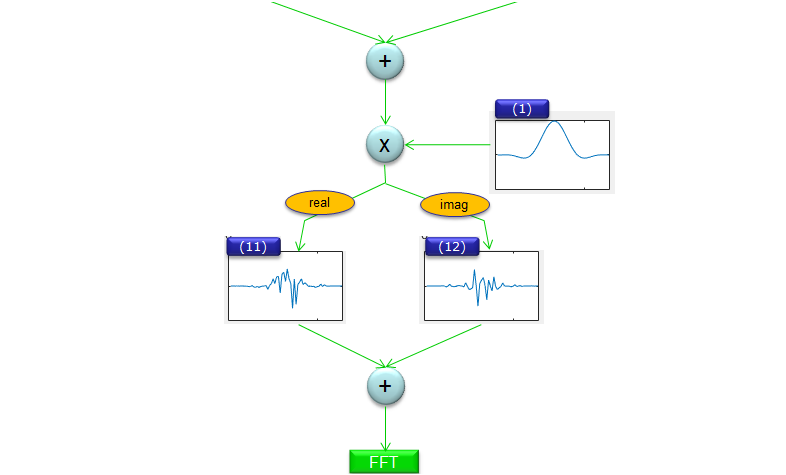
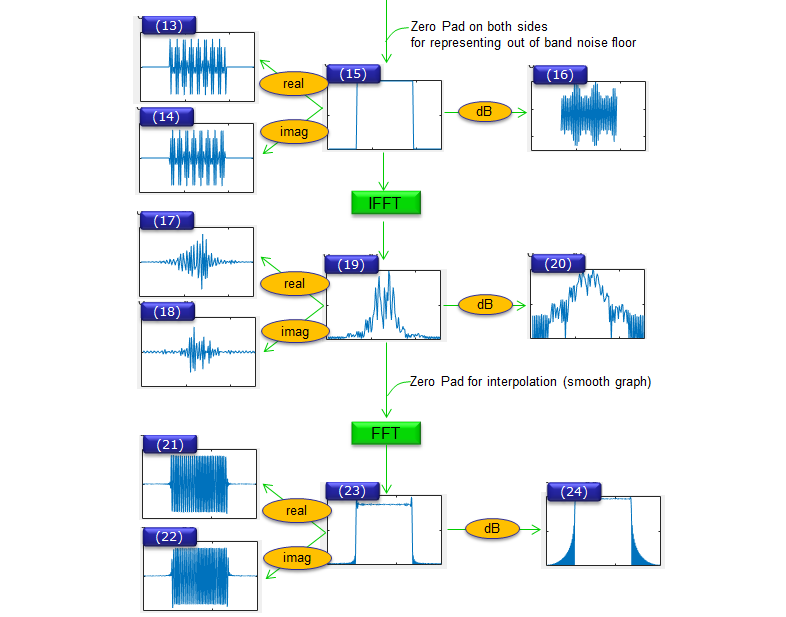
subplot(6,4,1); plot(h);xlim([0 length(h)]);set(gca,'yticklabel',[]); subplot(6,4,2); plot(s);xlim([-1.2 1.2]);ylim([-1.2 1.2]);set(gca,'yticklabel',[]); subplot(6,4,3); stem(real(s));xlim([1 length(s)]);ylim([-1.2 1.2]);set(gca,'yticklabel',[]); subplot(6,4,4); stem(imag(s));xlim([1 length(s)]);ylim([-1.2 1.2]);set(gca,'yticklabel',[]); subplot(6,4,5); plot(real(x));xlim([1 length(x)]);set(gca,'yticklabel',[]); subplot(6,4,6); plot(imag(x));xlim([1 length(x)]);set(gca,'yticklabel',[]); subplot(6,4,7); plot(real(x4));xlim([0 length(x4)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,8); plot(imag(x4));xlim([0 length(x4)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,9); plot(real(signal));xlim([0 length(signal)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,10); plot(imag(signal));xlim([0 length(signal)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,11); plot(real(y));xlim([0 length(y)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,12); plot(imag(y));xlim([0 length(y)]);ylim([-0.5 0.5]);set(gca,'yticklabel',[]); subplot(6,4,13); plot(real(yfft));xlim([0 length(yfft)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,14); plot(imag(yfft));xlim([0 length(yfft)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,15); plot(abs(yfft)/max(abs(yfft)));xlim([0 length(yfft)]);set(gca,'yticklabel',[]);%ylim([0 1]); subplot(6,4,16); plot(20*log(abs(yfft)/max(abs(yfft))));xlim([0 length(yfft)]);set(gca,'yticklabel',[]);%ylim([-10 0]); subplot(6,4,17); plot(real(yTx));xlim([0 length(yTx)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,18); plot(imag(yTx));xlim([0 length(yTx)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,19); plot(abs(yTx)/max(abs(yTx)));xlim([0 length(yTx)]);ylim([0 1]);set(gca,'yticklabel',[]); subplot(6,4,20); plot(20*log(abs(yTx)/max(abs(yTx))));xlim([0 length(yTx)]);ylim([-100 0]);set(gca,'yticklabel',[]); subplot(6,4,21); plot(real(yTxFreq));xlim([0 length(yTxFreq)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,22); plot(imag(yTxFreq));xlim([0 length(yTxFreq)]);set(gca,'yticklabel',[]);%ylim([-0.5 0.5]); subplot(6,4,23); plot(yTxFreqAbs);xlim([0 length(yTxFreqAbs)]);ylim([0 1]);set(gca,'yticklabel',[]); subplot(6,4,24);plot(yTxFreqAbsPwr); xlim([0 length(yTxFreqAbsPwr)]);ylim([-100 0]);set(gca,'yticklabel',[]); Following is the output of this code. The 'X' of subplot(6,4,X) corresponds to the number in following graphs. First, try to understand on your own the meaning of each of these plots based on the source code and then follow through my description. I know it looks complicated and confusing. You may take a look at the importants parts first and then get into details. (3), (4) is the I/Q data of symbols to be transmitted and like OFDM case (3),(4) is generated in frequency domain. (11),(12) is the I/Q part that is the output of FBMC process and these are time domain signal. All other plots before(13) are the ones generated in the middle of FBMC process and all the plots from (13) is just to show the frequency domain result of FBMC. (24) is the final outcome of FBMC process in frequency spectrum. Let me briefly go through each of the plots and see what they indicates. (1) - This is coefficients of Protocol Type Filter that will be used in FBMC process. (2) - This is the representation of (3), (4) in constellation (the constellation of data symbols to be transmitted). (3),(4) - These are the I/Q data of symbols to be transmitted and like OFDM case (3),(4) is generated in frequency domain. ((3) is real number, (4) is imaginary number) (5),(6) - These are the IFFT result of (3),(4), meaning the time domain representation of (3),(4). ((5) is real number, (6) is imaginary number) (7) - Four copies of (5) concatenated back-to-back. (I don't know why the author of the program did this) (8) - Four copies of (6) concatenated back-to-back. (I don't know why the author of the program did this) (9) - The result of multiplication of (1) and (7). It means this is filtered version of (7) (10) - The result of multiplication of (1) and (8). It means this is filtered version of (8) (11) - In this example, this is same as (9) because I set the variable 'Frame' to be '1', meaning Number of Frame is 1. (12) - In this example, this is same as (10) because I set the variable 'Frame' to be '1', meaning Number of Frame is 1. (13),(14) - This is the FFT result of '(11),(12)' in linear scale. ((13) is real number, (14) is imaginary number) (15) - This is the FFT result of (11),(12) in linear Magintude with Zero pad on both sides.. (16) - This is the magnified view of passband part of (15) (17),(18) - This is the real and imanaginary number of IFFT result of (15). (19) - This is the magnitude of IFFT result of (15) (20) - This is the representation of (19) in dB scale. (21),(22) - This is the real and imanaginary number of FFT result of (19) with more zero padding for smoothing. (23) - This is the magnitude of (21),(22) (24) - This is the representation of (23) in dB scale.
Following shows how each of the plots are produced along the each steps of FBMC waveform generation. I hope this would be clearer than any verbal (written description). Just putting the important milestone points, (2) is the bit stream mapped to a sequence of complex data and represnted in constallation. (1) is Pulse Shaping Filter. (19) is the time domain physical signal being transmitted through the antenna after upconversion. (21) is the time domain physical signal being transmitted through the antenna after upconversion.
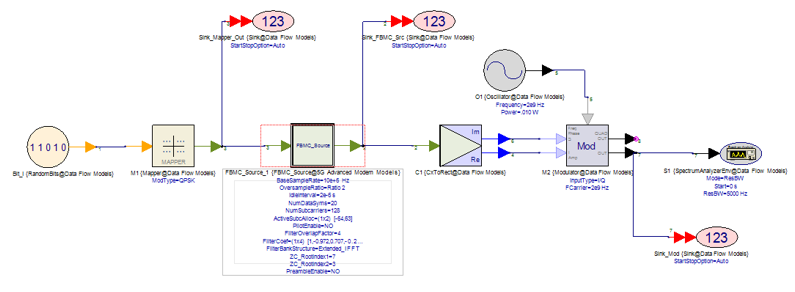
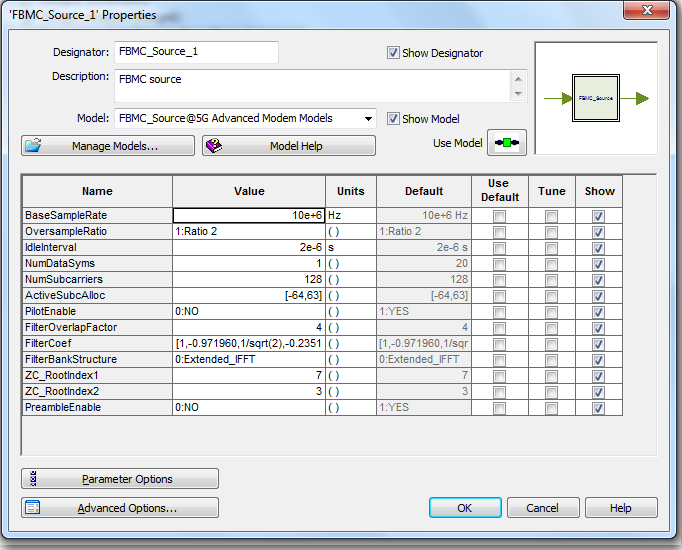
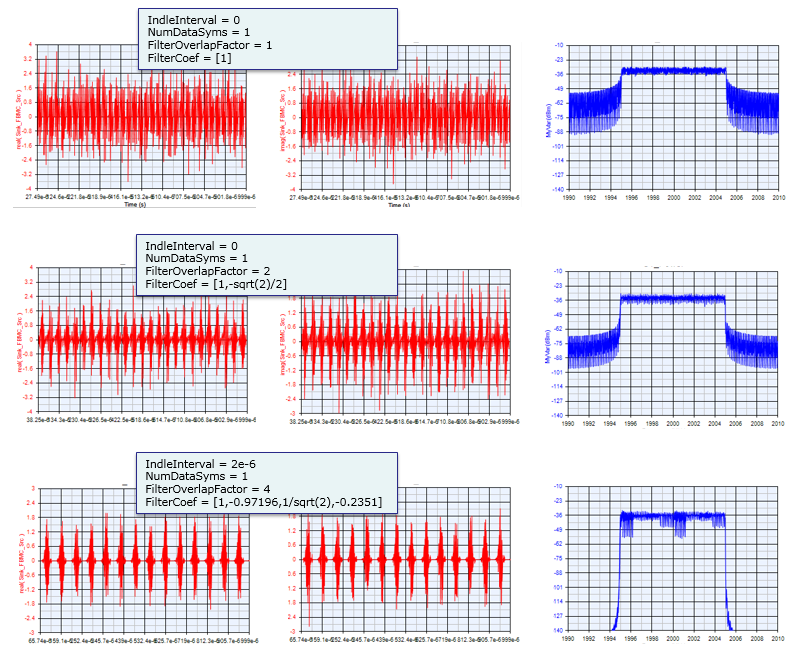
Example 02 > --------------------------------------------------------------------------------------------------- Following is another example for FBMC that I created with SystemVue(Keysight). You may purchase or get trial license of the software and play with it. It will give you more concrete/intuitive understanding of factors for FBMC (SystemVue document says this library is based on Ref [4]. So you may look into the reference if you are interested in technical details.
Reference[1] GFDM Interference Cancellation for Flexible Cognitive Radio PHY Design R. Datta, N. Michailow, M. Lentmaier and G. Fettweis Vodafone Chair Mobile Communications Systems, Dresden University of Technology, 01069 Dresden, Germany Email:[rohit.datta, nicola.michailow, michael.lentmaier, fettweis]@ifn.et.tu-dresden.de [2] 5G NOW. D3.1 5G Waveform Candidate Selection [3] Waveform Contenders for 5G - suitability for short packet and low latency transmissions. Frank Schaich, Thorsten Wild, Yegian Chen Alcatel-Lucent AG Bell Labs Stuttgart, Germany [4] FBMC Physical Layer : a Primer PHYDYAS [5] Matlab Centeral : FBMC Modulation / Demodulation (with BSD Copyright) Copyright (c) 2014, Michel TERRE
All rights reserved.
|
||