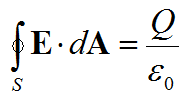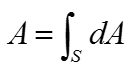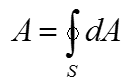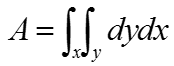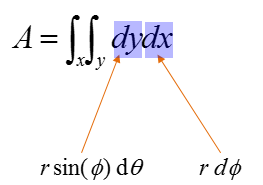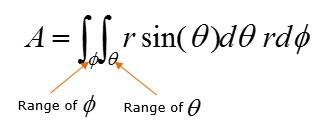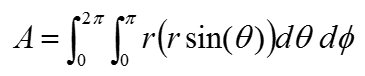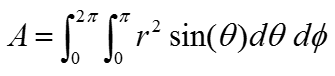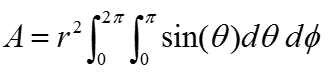|
Engineering Math - Calculus |
||
|
Surface Integral
If you are new to the concept of Integration, I would suggest you to read the "Integration" page first.
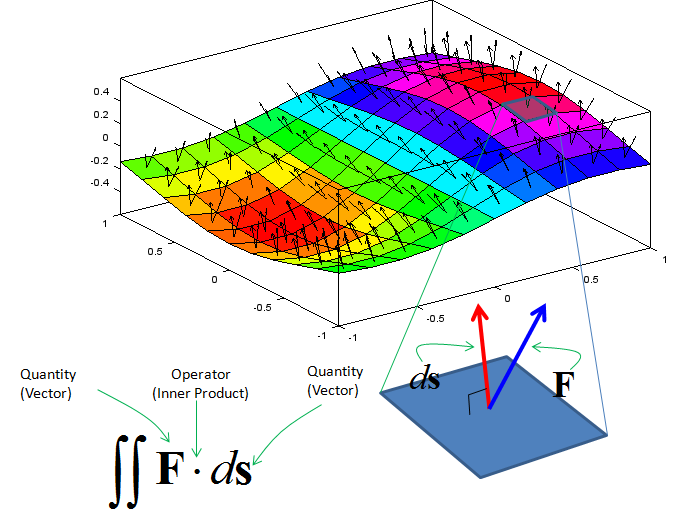
As you may guess from the word itself, surface integral is a type of integraion taken over a surface. There can be many different operations over a surface. One example is as shown below. In this example, you see two vectors in each segments of the surface. one of the vector is normal to each surface segment(This vector is called 'normal vector'). The other vector is an arbitrary angle to the normal vector . Now I want to take the inner product of each red vector and blue vector and sum them all. This operation can be represented in a mathematical form as shown below. The mathematical operation is exactly same as the one shown in previous example. The only differences is that this operation goes along the surface. This kind of integration is called "Surface Integral".
Followings are some of the exaples that uses the surface integral and I will keep adding more examples as I have chance. These examples would not be a completely new one. You would find these examples from the various textbook, but I would explain it in my own way and hopefully help you to understand more easily and intuitively.
Examples 01 > Gauss Law
One of the most common example of surface integral is Gauss Law of electric field which is expressed as shown below. (This is one component of Maxwell equations in electromagnetic theory).
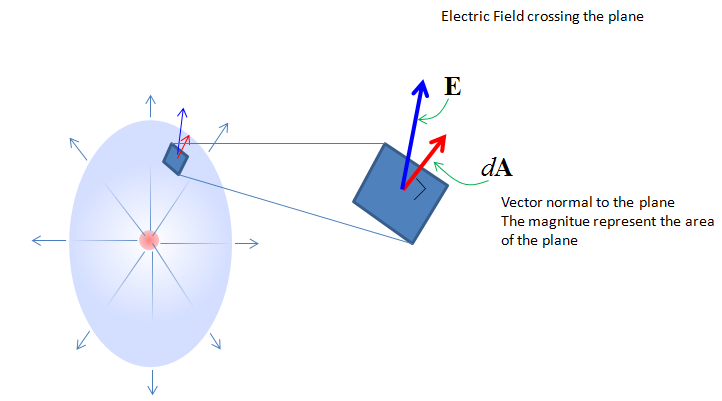
Meaning of the left hand part of the equation (Integration Part) is as shown below. Suppose that you have a closed surface (like a sphere) and put a charge inside of the closed surface. Then the electric field line goes out of the charge (if the charge is positive) and penerate out of the closed surface. If you take a small segment (rectangular plane) of the surface, you will see the field line going through the surface with a certain angle to the plane. The angle between the field line and the surface is defined by the inner product of the normal vector and the field line. If you take the inner product of the two vectors of each segnment accorss the whole surface, it give you the value of the left hand side of the equation.
Examples 02 > Surface Area of a Sphere
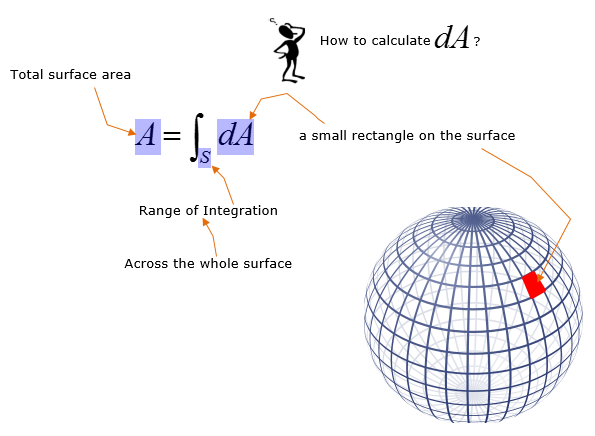
This example itself would be one of the most common one you may see in your multi-variable calculus textbook. But I want to explain it in a little bit different way from what you see in the textbook (hopefully my explanation would help you better to understand this example). The question given to you in this example is 'what is the total surface area of the sphere shown below ?'.
If you have any basic concept of integration and understand you can apply the concept to solve this problem, you may easily come up with the idea that 'if I split the shole surface into a lot of small area and sum up all of those small area across the whole surface, you can get the total area of the surface'. The first step is to turn this into mathematical form. When you do this, I would suggest you not to worry too much of how to solve it. If you think too much of getting the solution from the first place, you would have more trouble reaching to the solution. My first mathematical interpretation for the satement 'split the shole surface into a lot of small area and sum up all of those small area across the whole surface' is as follows. Isn't it simple ?
Or you may write it as follows.
The meaning of this expression can be illustrated as below. I hope this illustration and short comments on it is good enough for your understanding.
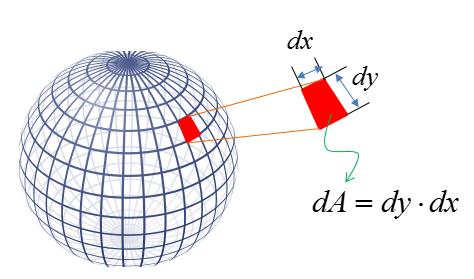
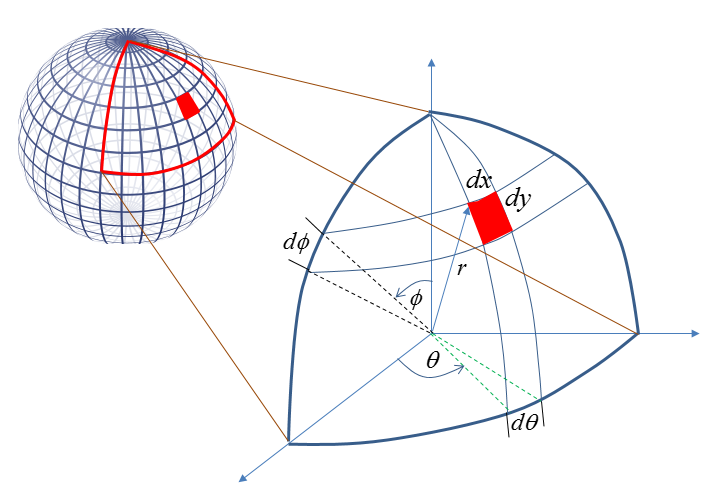
The expression written above is very simple and not so much scary, it does not have much details on getting the specific solution. In order to bring you closer to the specific solution, I would break down the term dA into more detailed parameters as shown below. If you assume that the red shape is a rectangle, the area (dA) can be calculated by (dx * dy). In this illustration, the red area would not look like a rectangle (it would look like a trapezoid), however if you break down the area very small you can approximate it as a rectangle.
Now let's rewrite the equation by replacing the term dA with dy dx. It becomes as follows. Since the single variable dA has become two variable (dx dy), the number of integral symbol becomes two as well. Getting scared ? Don't worry.. I would not solve this equation for now.. just try to understand the meaning of the equation.
Now the next step is to figure out how to figure out the dx and dy. In order to do this, I would need to expand the picture and put many lines and labels as shown below. However, you would need to put your own effort on this to clearly understand the meaning of each labels and lines. It is difficult to show you the 3 dimensional object into 2 dimensional surface (the monitor). Actualy even if you see this in real 3D space, it would not be so easy unless you put some of your own effort.
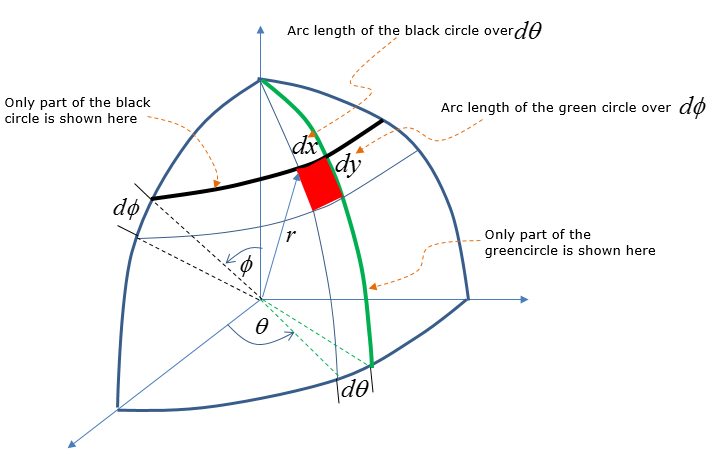
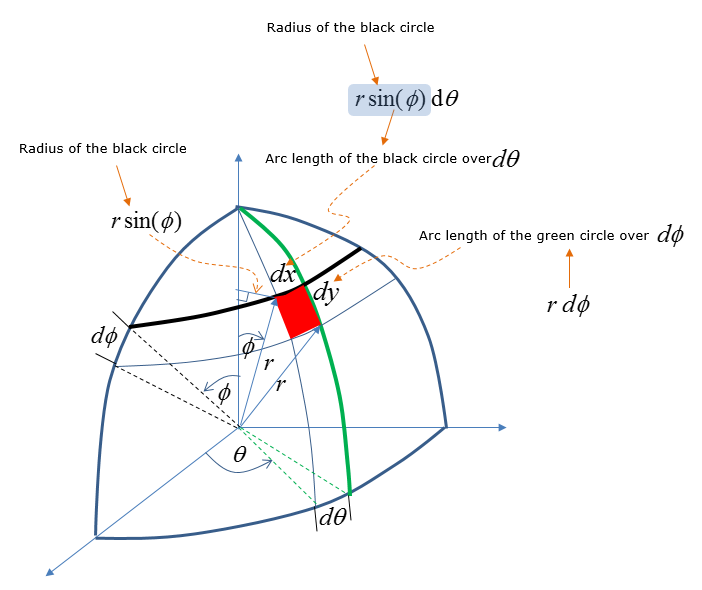
Using the additional lines and parameters (i.e, radius, angles), you can figure out dx and dy as shown below. In this figure, dx and dy is calculated by the arc length. As you know, an arc is not the straight line.. but if you make the red area small enough you can approximate the arc as a straight line that represents a side of a rectangle.
From the high school math (junior high school or senior high school depending on where you are educated), you would remember that you can calculate the length of an arc on the circumference of a circle from the radius and angle.(If you arleady forgot about this, like me :), refer to the definition of arc length page in www.mathisfun.com ). Using this arc length calculation method, you can figure out dx and dy as shown below. It would take some time and effort for you to understand how dx and dy can be written as follows. But this is the most important step. So make it sure that you clearly understand this figure before you move any further.
With this new expression, you can label the dx and dy in the equation as shown below.
If you repalce the term dx and dy with the new information you get, the equation should become as below.
Now let's specify the range of the two angles. I don't have any good idea to show this range clearly in two dimentional drawing. Just for the conclusion the range of the two angle is specified as follows. Think of how this range came out on your own. You may not get it just in a couple of seconds.. but if you keep thinking I think you can figure it out in several minutes. Specifying the range of the angle and with a little bit of rewriting, you would get following equation.
Simplifying the equation just a little bit, you can rewrite it as shown below.
In case of sphere, the radius r is same in every point on the surface. it means the r is a constant. So you can pull out the r term out of the integration as below. (If the shape of the object is not a sphere where r changes depending on location, just put the r as shown above).
|
||