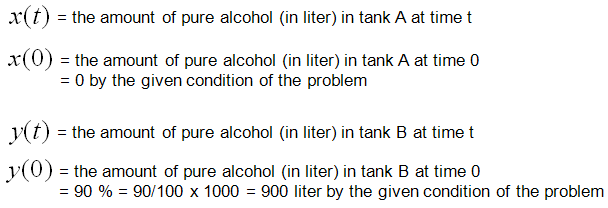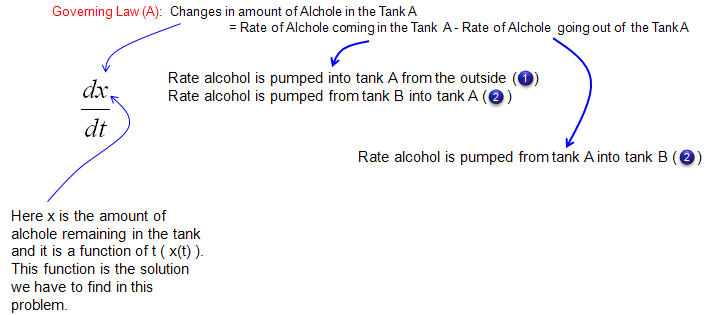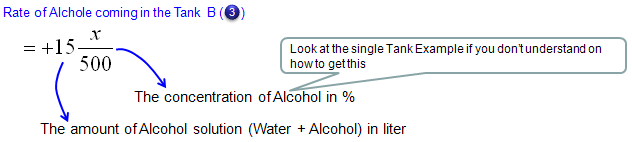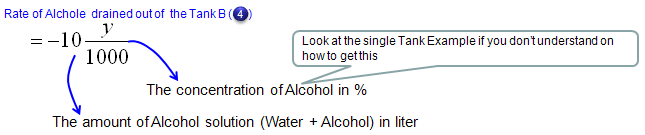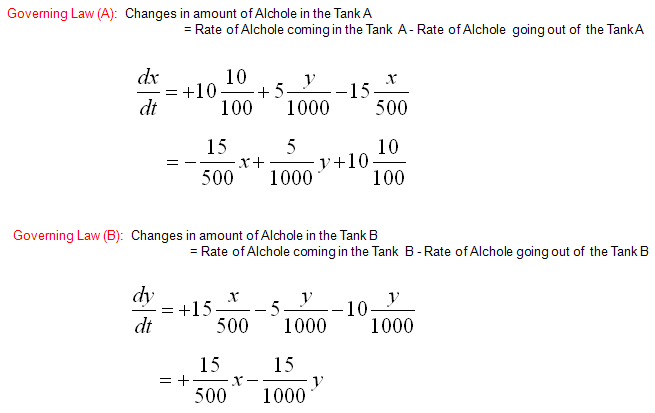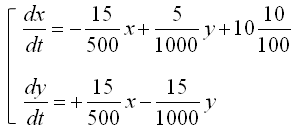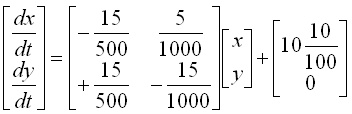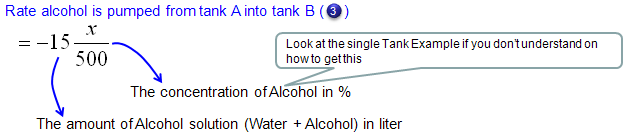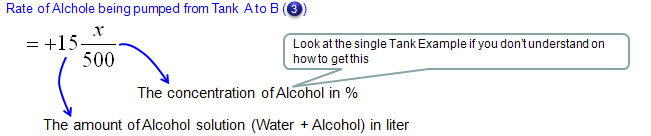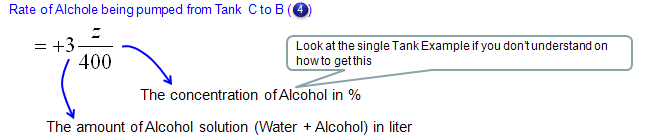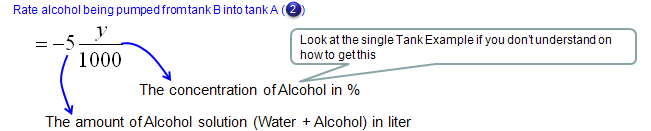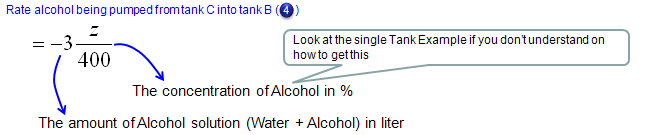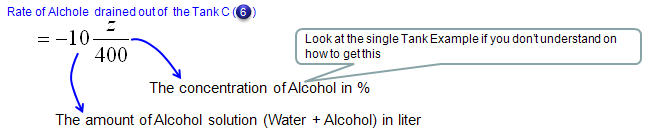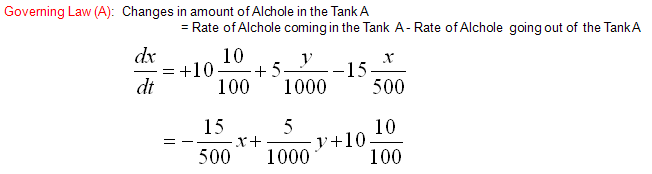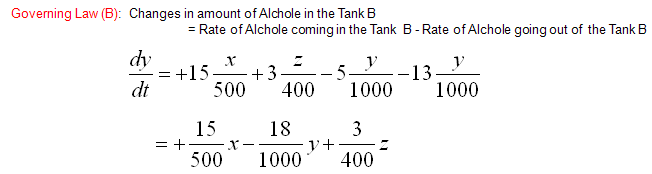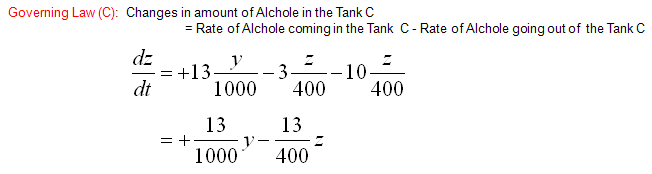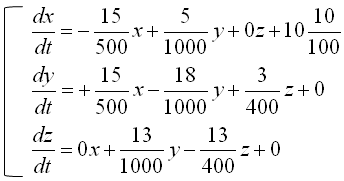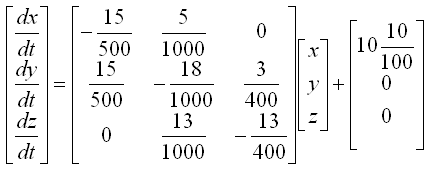A mixing problem asks how the amount of a dissolved material in a tank changes while solution flows in and out. The governing law is a simple balance. The rate of change equals the rate coming in minus the rate going out. Each tank adds one unknown and one equation. So a single tank gives one first order differential equation, and connected tanks give a system of first order equations.
The Modeling examples in this page are :
Example : Mixing Problem
This is one of the most common problems for differential equation course. You will see the same or similar type of examples from almost any books on differential equations under the title/label of "Tank problem", "Mixing Problem" or "Compartment Problem". But I think (hope) I will be providing the most detailed / step-by-step explanation -:)
To be honest I was not so good at solving this kind of problems when I first studying the problem even though it is only simple first order differential equation. Come to think of it, the reason why I was not so good at this was because I didn't clearly understand the steps through which we generate a differential equation from the description of the problem. That is, I was not so good at the modeling process.
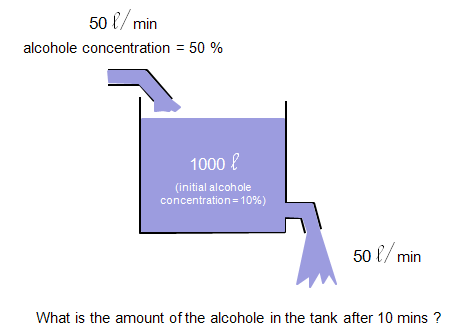
One example for this kind of problems is as follows :
i) There is a tank which has a mixture of Water and Alcohole. (Total volume of the mixture(solution) is 1000 liter).
ii) The initial concentration of Alcohol is 10 % (it means that Water is solvent and Alcohol is solute)
iii) There is an outlet through which the solution is going out at the rate of 50 liter/min.
iv) There is an inlet through which a solution (mixture of water and alcohol) is coming in at the rate of 50 liter/min. The concentration of the alcohol in the incoming solution is 50%.
The question is what will be the concentration of the alcohol of the solution in the tank after 10 mins ?
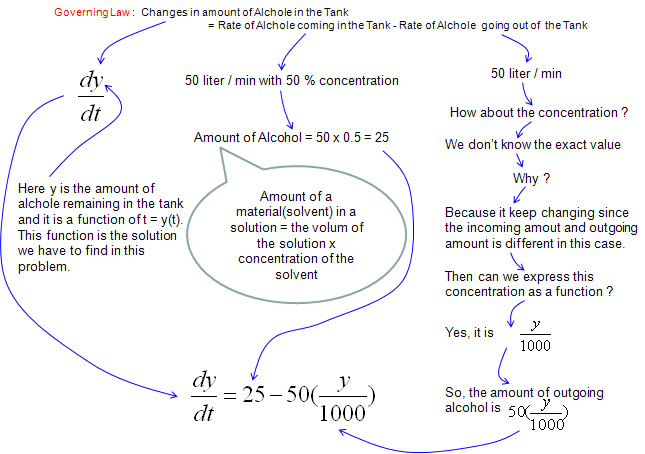
The process of deducing the differential equation (modeling) is as follows. I think you have already went through a couple of examples of this kind in your Differential equation course (or you can search several tutorials of this kind in the internet) and see if the following process that I put down makes any sense to you.
Note : Don't you have any question at this point ? If you have the question saying "In the description of the problem, I see the statement 'the initial concentration of alcohol in the tank is 10%', but I don't see this condition is being used in the derivation of the equation. Does this mean that this initial condition is useless ?"
We don't need the initial condition at least for modeling process (the process of deriving the differential equation), but we need the initial condition when we solve the equation to get a specific values from the solution. (In this problem, the initial condition y(0) = 1000 liter of solution x 0.1 (10 % of concentration of alcohol) = 100).
Now let's finish the problem and answer the question. The equation dy/dt = 25 - 50(y/1000) is the same as dy/dt = 25 - 0.05y. The tank is in balance when dy/dt = 0. This happens at y = 500 liter, which is a concentration of 50 %. That is the concentration of the incoming solution, as you would expect. With the initial condition y(0) = 100, the solution is y(t) = 500 - 400e-0.05t.
At t = 10 min, y(10) = 500 - 400e-0.5 = 257.4 liter. So the concentration of alcohol in the tank after 10 mins is 257.4/1000, or about 25.7 %. The amount of alcohol moves from 100 liter toward 500 liter, and the gap shrinks with the time constant 1000/50 = 20 min. For example, the tank reaches 40 % (400 liter) only at t = 20 ln 4, which is about 27.7 min.
One label in the governing law diagram of this example needs a correction. The speech balloon says "material(solvent)" and "concentration of the solvent". The material we track is alcohol, and alcohol is the solute, as item ii) of the problem states. So read the balloon as: amount of solute = volume of the solution x concentration of the solute.
A mixing equation is a balance of rates : dy/dt = rate in - rate out. The rate out is the outflow rate multiplied by the concentration in the tank, y/1000 here.The tank moves toward the inflow concentration : With equal inflow and outflow, the steady state is the inflow concentration, 50 % here. The initial concentration does not change the end point.The time constant is the volume divided by the flow rate : 1000 liter / 50 liter/min = 20 min. After 10 min, the tank has covered 1 - e-0.5, about 39 %, of the way from 10 % to 50 %.
Example : Mixing Problem - Two Tank
If you haven't read the previous example (One Tank example), please go through it first and get back to this example and try to find what is the difference and what is common. and more importantly try to find some pattern of extending the logic of thinking on modeling.
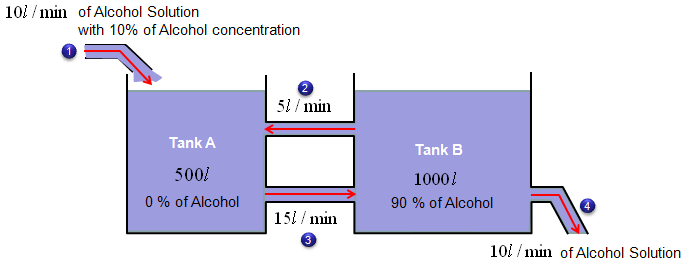
Now we have another tank (the second tank) get connected to the first tank that I used in previous example. First, just take brief look at the diagrame espectiall the direction of arrows.
i) There are two tanks which has a mixture of Water and Alcohole. (Total volume of the mixture(solution) of Tank A is 500 liter and the volume of Tank B is 1000 litter).
ii) The initial concentration of Alcohol for Tank A is 0 % (it means that pure Water)
iii) The initial concentration of Alcohol for Tank B is 90 %
iv) There is an outlet for Tank A through which the solution is going out at the rate of 15 liter/min.
v) There are two outlets for Tank B and the solution is going out at the rate of 5 liter/min through one outlet and the solution is going out at the rate of 10 liter/min through the other outlet.
vi) There are two inlets for Tank A. A solution (mixture of water and alcohol) is coming in at the rate of 10 liter/min with the concentration of 10 % through one inlet and solution (mixture of water and alcohol) is coming in at the rate of 5 liter/min with the yet unknown concentration through one inlet.
vii) There are one inlet for Tank B. A solution (mixture of water and alcohol) is coming in at the rate of 15 liter/min with the yet unknown concentration through the inlet.
The question is what will be the concentration of the alcohol of the solution in the tank A and Tank B after 10 mins ?
Before jumping into the modeling process, let me give you a couple of questions that can easily be overlooked but important.
Would the volume of solution for each tank change over time ?
The answer is NO, the volume does not change over time. Most of this kind of problem from the text book are carefully designed so that the volum of tank does not change over time.
Why do they set the problem so that the volum of the solution in the tank does not change ?
It is because the mathematical equation will simpler under that condition.
Let's summarize some of the initial conditions and define some of the variables for modeling.
Now let's look into the governing law of this problem.
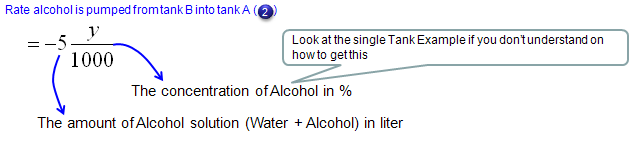
The rule is as follows and you will notice that this law is exactly same as what you saw in previous example (Single Tank case). The only difference is that Tank A has one more inlet.
Next step is to describe the amount of alcohol coming in and out of the tank A in mathmatical terms as follows. Overall the expressions are simple. The only thing you have to think a little bit is the expression for the concentration of alcohol for each tank. They are expressed as x/500 and y/1000. These can be expressed in this kind of simple manner because we set the problem so that the total amount of solution for each tank does not change over time. If the total volume of each tank changes, you cannot express it as a simple number like '500' or '1000'. You would need the functions (a function of t) describing the volume of each tank over time.
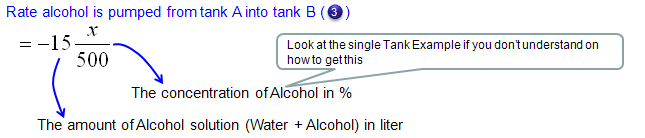
Now let's look into governing law for Tank B. Overall process is as follows and you will notice that the process (logic) is exactly same as you did for Tank A.
Mathematical expression of each terms of governing law (governing equation) are as follows.
Now we have each terms (components) of governing law for Tank A and Tank B. If you just combine those components according to the governing law you will get the following two differential equation.
Writing again the two equations into a simultaneous equation (system equation), we get the following.
This is done with modeling and you can solve the equations as it is, but some software require the system equations to be input in matrix format as follows.
Let's solve this system and answer the question for 10 mins. The initial values are x(0) = 0 and y(0) = 900 liter. The matrix has two negative eigenvalues, about -0.0369 and -0.0081 per min, so both tanks settle to a steady state. At the steady state both derivatives are zero. Solving the two equations then gives x = 50 liter and y = 100 liter. This is a concentration of 10 % in both tanks, the same as the only inflow from the outside.
The approach is slow compared with 10 mins, because the smaller eigenvalue has a time constant of about 1/0.0081 = 123 min. A numerical solution gives x(10) = 44.7 liter and y(10) = 781.5 liter. So after 10 mins, the concentration is about 8.9 % in Tank A and about 78.1 % in Tank B. Tank A does not stop at 10 %, though. It keeps receiving strong solution from Tank B through inlet 2, and it peaks at about 21.8 % near t = 64 min before it comes back down toward 10 %.
One label in the governing law diagram for Tank A needs a correction. The outgoing term, the flow from Tank A into Tank B, carries the circle 2 there. In the tank diagram this flow is circle 3, and the image with the term -15 x/500 uses circle 3 correctly.
Each tank gives one equation : A flow between two tanks appears twice. It has a minus sign in the tank it leaves and a plus sign in the tank it enters, for example -15x/500 in dx/dt and +15x/500 in dy/dt.Check the volume balance first : Tank A receives 10 + 5 = 15 liter/min and loses 15 liter/min. Tank B receives 15 liter/min and loses 5 + 10 = 15 liter/min. This balance is what allows the fixed volumes 500 and 1000 in the denominators.The eigenvalues set the time scale : Both eigenvalues are negative, so the system is stable. The slower one, -0.0081 per min, decides how long both tanks need to reach 10 %.
Example : Mixing Problem - Three Tanks
This is one-step further extention of the previous example. (Make it sure that you have gone through the previous two examples - single tank, two tank problems before you start this example).
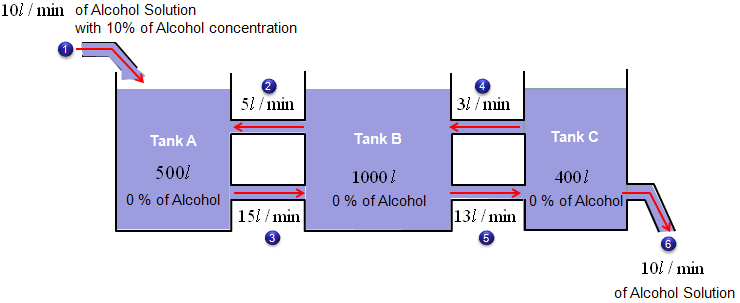
Now we have another tank (the third tank) get connected to the second tank that I used in previous example. First, just take brief look at the diagrame espectiall the direction of arrows.
i) There are three tanks which has a mixture of Water and Alcohole. (Total volume of the mixture(solution) of Tank A is 500 liter and the volume of Tank B is 1000 litter and the volume of Tank C is 400 litter).
ii) The initial concentration of Alcohol for Tank A is 0 % (it means that pure Water)
iii) The initial concentration of Alcohol for Tank B is 0 % (it means that pure Water)
iv) The initial concentration of Alcohol for Tank C is 0 % (it means that pure Water)
v) There is an outlet for Tank A through which the solution is going out at the rate of 15 liter/min.
vi) There are two outlets for Tank B and the solution is going out at the rate of 5 liter/min through one outlet and the solution is going out at the rate of 13 liter/min through the other outlet.
vii) There are two outlets for Tank C and the solution is going out at the rate of 3 liter/min through one outlet and the solution is going out at the rate of 10 liter/min through the other outlet.
viii) There are two inlets for Tank A. A solution (mixture of water and alcohol) is coming in at the rate of 10 liter/min with the concentration of 10 % through one inlet and solution (mixture of water and alcohol) is coming in at the rate of 5 liter/min with the yet unknown concentration through one inlet.
ix) There are two inlet for Tank B. A solution (mixture of water and alcohol) is coming in at the rate of 15 liter/min with the yet unknown concentration through the inlet and solution (mixture of water and alcohol) is coming in at the rate of 3 liter/min with the yet unknown concentration through one inlet..
x) There is one inlet for Tank C. A solution (mixture of water and alcohol) is coming in at the rate of 13 liter/min with the yet unknown concentration through the inlet
The question is what will be the concentration of the alcohol of the solution in the tank A,Tank B and Tank C after 10 mins ?
Before jumping into the modeling process, let me give you a couple of questions that can easily be overlooked but important.
Would the volume of solution for each tank change over time ?
The answer is NO, the volume does not change over time. Most of this kind of problem from the text book are carefully designed so that the volum of tank does not change over time.
Why do they set the problem so that the volum of the solution in the tank does not change ?
It is because the mathematical equation will simpler under that condition.
Let's summarize some of the initial conditions and define some of the variables for modeling.
Now let's look into the governing law of this problem.
The rule is as follows and you will notice that this law is exactly same as what you saw in previous example (Two Tank case).
Next step is to describe the amount of alcohol coming in and out of the tank A in mathmatical terms as follows. Overall the expressions are simple. The only thing you have to think a little bit is the expression for the concentration of alcohol for each tank. They are expressed as x/500 and y/1000. These can be expressed in this kind of simple manner because we set the problem so that the total amount of solution for each tank does not change over time. If the total volume of each tank changes, you cannot express it as a simple number like '500' or '1000'. You would need the functions (a function of t) describing the volume of each tank over time.
Now let's look into governing law for Tank B. Overall process is as follows and you will notice that the process (logic) is exactly same as you did for Tank A.
Mathematical expression of each terms of governing law (governing equation) are as follows.
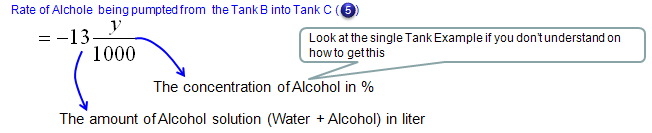
Now let's look into governing law for Tank C. Overall process is as follows and you will notice that the process (logic) is exactly same as you did for Tank A.
Mathematical expression of each terms of governing law (governing equation) are as follows.
Now we have each terms (components) of governing law for Tank A,Tank B and Tank C. If you just combine those components according to the governing law you will get the following three differential equation.
Writing again the three equations into a simultaneous equation (system equation), we get the following.
This is done with modeling and you can solve the equations as it is, but some software require the system equations to be input in matrix format as follows.
Let's look at the structure of this matrix before solving it. Tank A exchanges solution only with Tank B, and Tank C exchanges solution only with Tank B. So the corner entries are zero and the matrix is tridiagonal. Also, each column adds up to minus the outflow to the outside divided by the tank volume. The columns for Tank A and Tank B add up to 0, and the column for Tank C adds up to -10/400. This is how the matrix keeps track of the alcohol that leaves through outlet 6.
Now the numbers. The eigenvalues are about -0.0075, -0.0314 and -0.0416 per min, so the system is stable again. The steady state is x = 50, y = 100 and z = 40 liter, which is 10 % in all three tanks. All three tanks start with pure water, and alcohol enters only through inlet 1. So alcohol has to pass Tank A before it reaches Tank B, and Tank B before it reaches Tank C. A numerical solution at t = 10 min gives x = 8.66, y = 1.28 and z = 0.053 liter. The concentrations are about 1.73 % in Tank A, 0.13 % in Tank B and 0.013 % in Tank C.
In the governing law diagram for Tank C, the note at the lower left says "Here y is the amount of alchole". For Tank C it should read z, as the function z(t) in the same note shows.
A chain of tanks gives a tridiagonal matrix : Each tank is connected only to its neighbours, so each row has at most three non-zero entries.Column sums show where material leaves : A column adds up to zero when the tank sends everything to other tanks. It adds up to minus the drain rate over the volume when the tank drains to the outside.Alcohol arrives with a delay along the chain : After 10 min, the concentration falls by roughly a factor of ten from each tank to the next. Each tank receives only what the previous one has already collected.The slowest eigenvalue decides the settling time : The time constant of -0.0075 per min is about 134 min. All three tanks need several hours to approach 10 %.