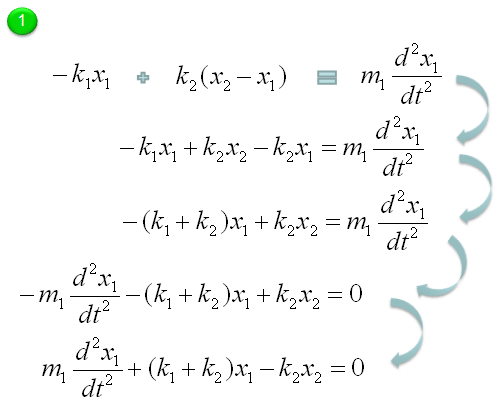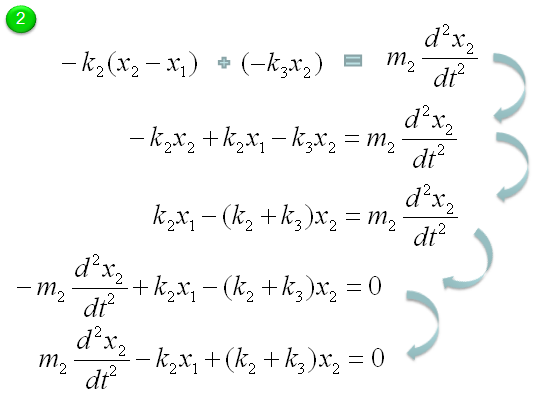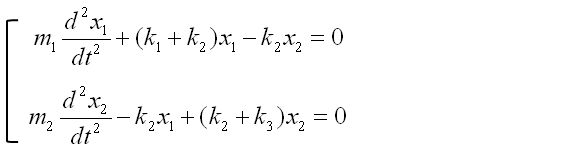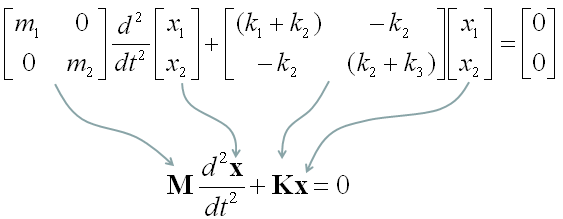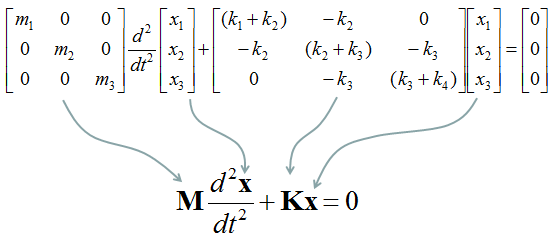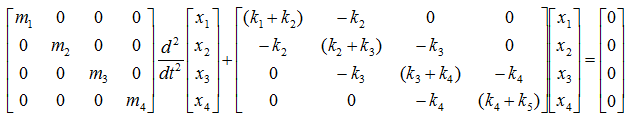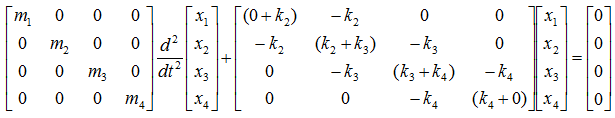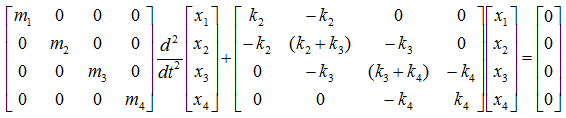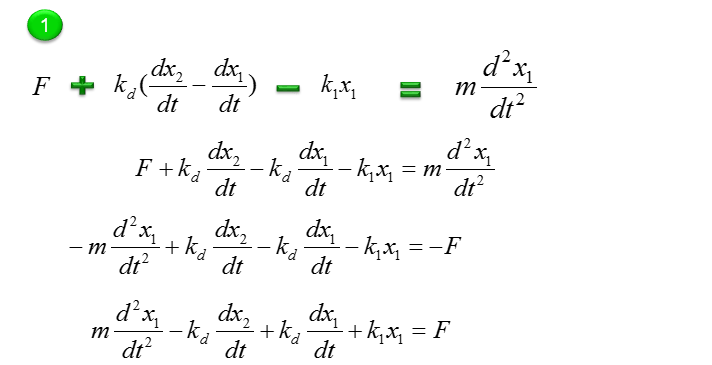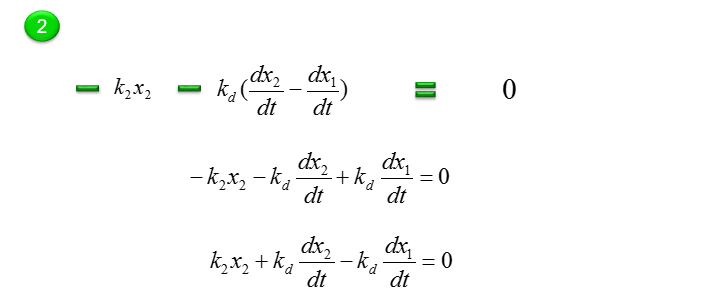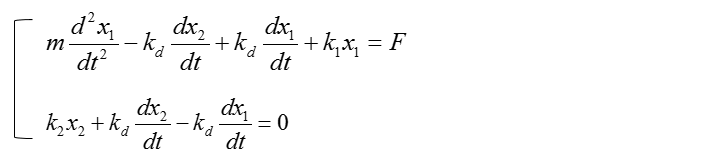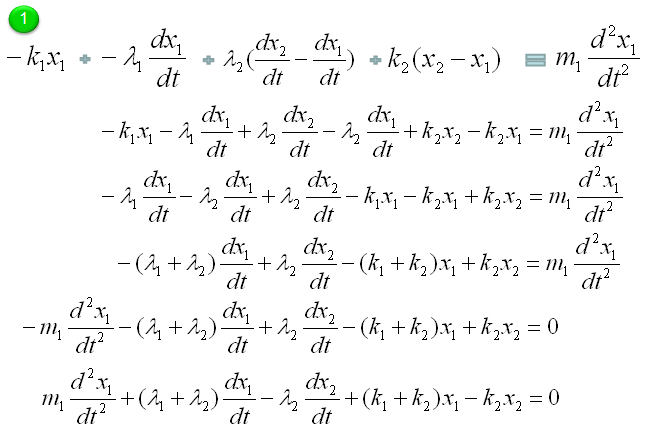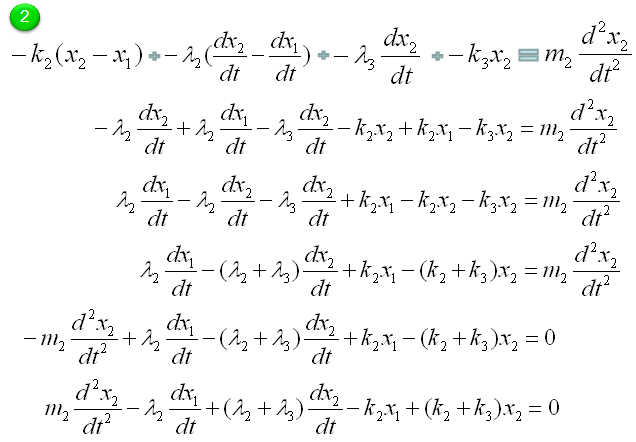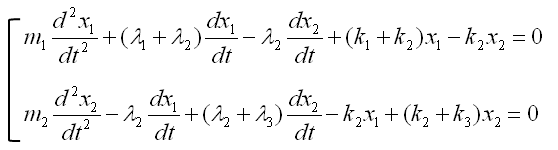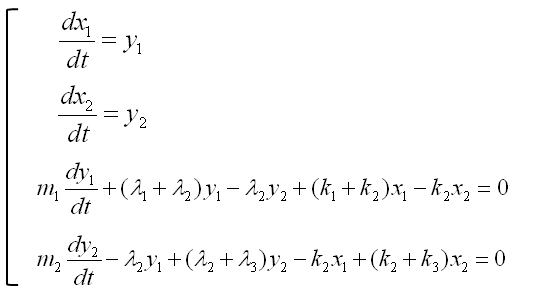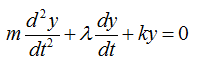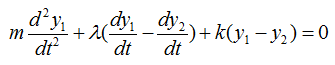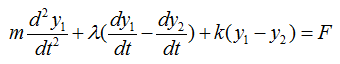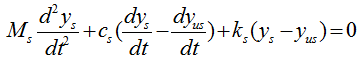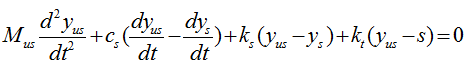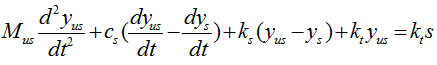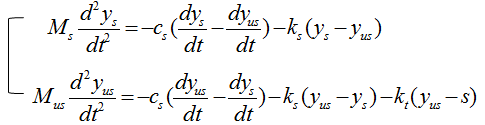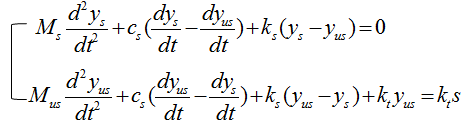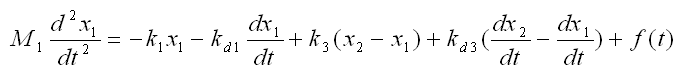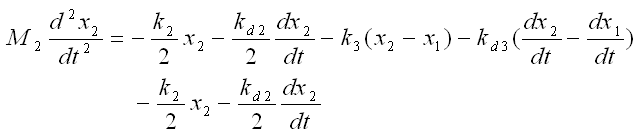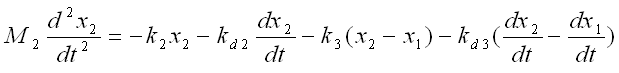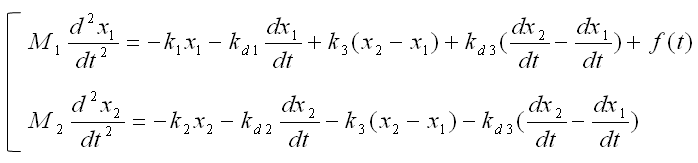|
Engineering Math - Differential Equation |
||
|
Spring Mass Model
Spring mass problem would be the most common and most important example as the same time in differential equation. Especially you are studying or working in mechanical engineering, you would be very familiar with this kind of model.
The Modeling Examples in this Page are :
The examples in this section is almost same as what you've learned in high school physics. The only difference is that in high school physics they don't teach anything about differential equation. So they just show you the final conclusion of the mathematical modeling without using differential terms. However, the physical model is exactly same.
< Example : Simple Harmonic Motion - Vertical Motion>
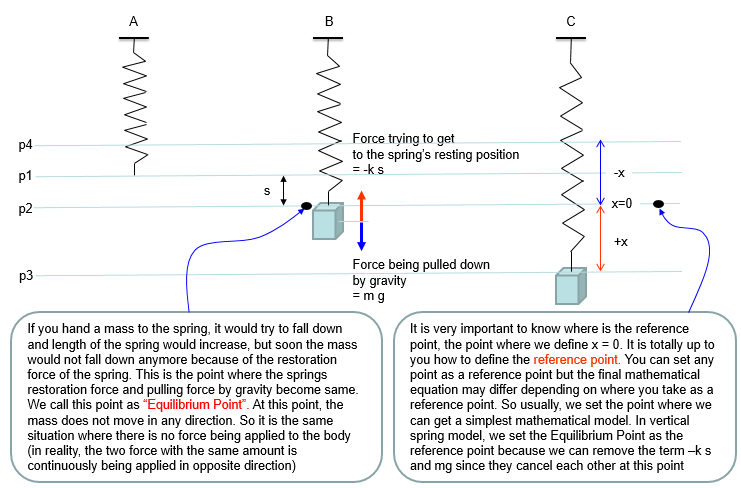
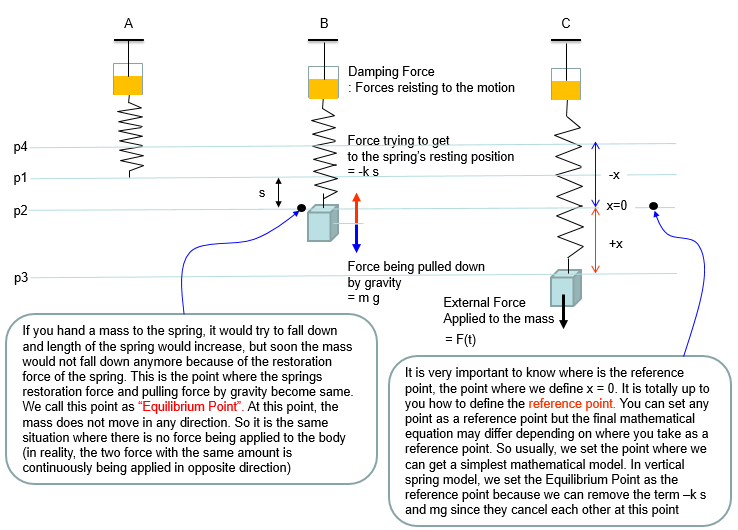
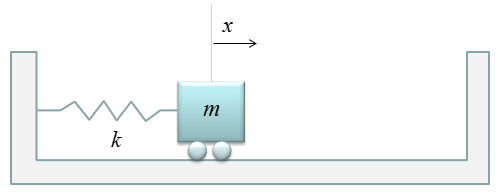
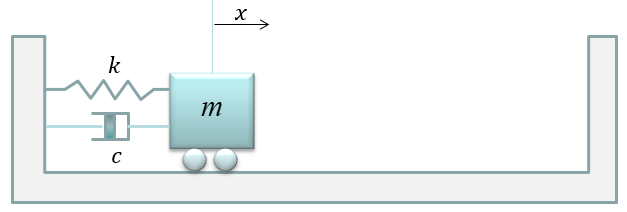
This is one of the most famous example of differential equation. Probably you may already learned about general behavior of this kind of spring mass system in high school physics in relation to Hook's Law or Harmonic Motion. Of course, you may not heard anything about 'Differential Equation' in the high school physics. (As for the general introduction of this system, see this excelent video and get some intuitive idea on the system: Mechanical Universe 16 - Harmonic Motion. If this link does not work, try searching in YouTube with the keyword 'Mechanical Universe 16 - Harmonic Motion').
The example in this section is about ideal case of single spring and single mass system and it is assumed that there is no friction , no damping.. i.e there is nothing that oppose the motion of each component (spring and mass). In reality, you cannot have this kind of idea system. However, a lot of textbook (other materials) about differential equation would start with these example mainly because these would give you the most fundamental form of differential equations based on Newton's second law and a lot of real life examples are derived from these examples just by adding some realistic factors (e.g, damping , frictions , external forces etc).
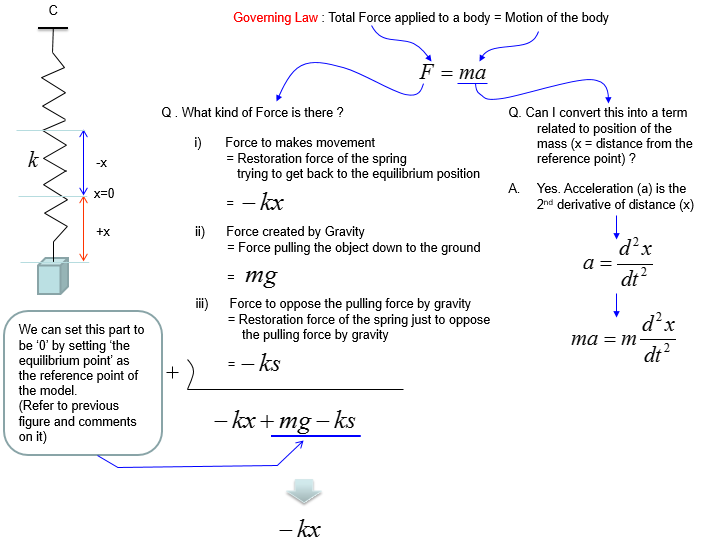
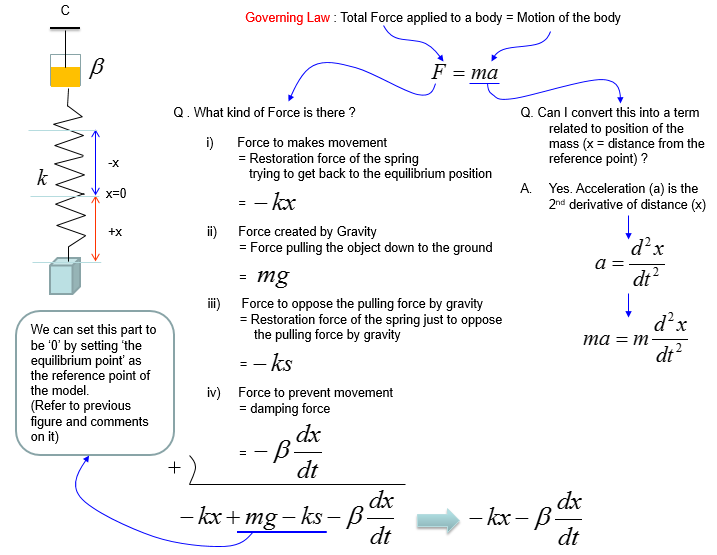
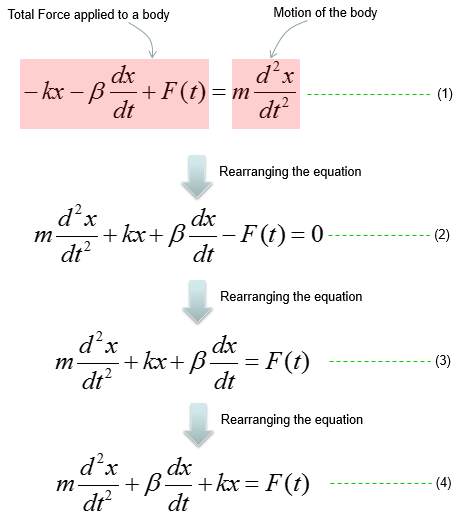
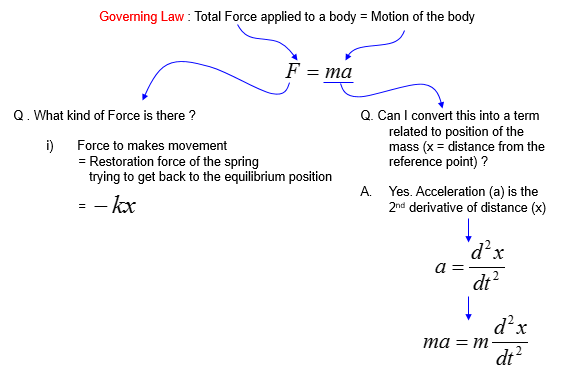
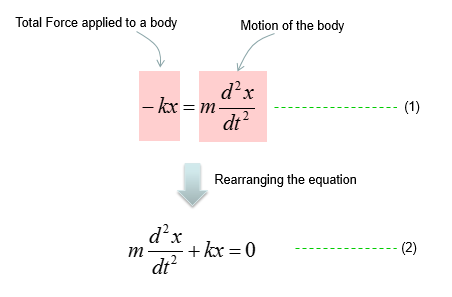
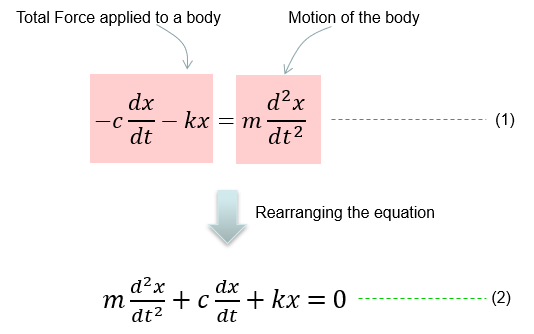
Based on the governing equation for this system, you would be able to list up all the component forces acting upon the system as shown below.
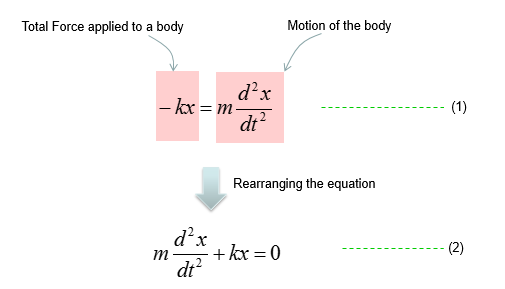
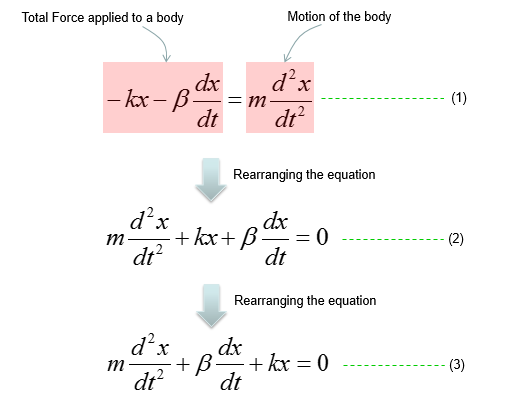
Combining these two parts you will get the equation as (1) and with a little bit of rearrangement you will get the equation as (2). You may ask "Do I have to rearrange (1) always ?". The answer is NO. The equation (1) and (2) are completely same. The physical interpretation of (1) and (2) may vary a little bit, but mathemtically they are same. You will see both forms for the exactly same physical model in various material(e.g, textbook, internet etc).
Solution : Solution to this equation in graphical form is posted in my visual note. It is presented in multiple cases depending on change of each parameters as listed below.
< Example : Simple Harmonic Motion - Vertical Motion with Damping >
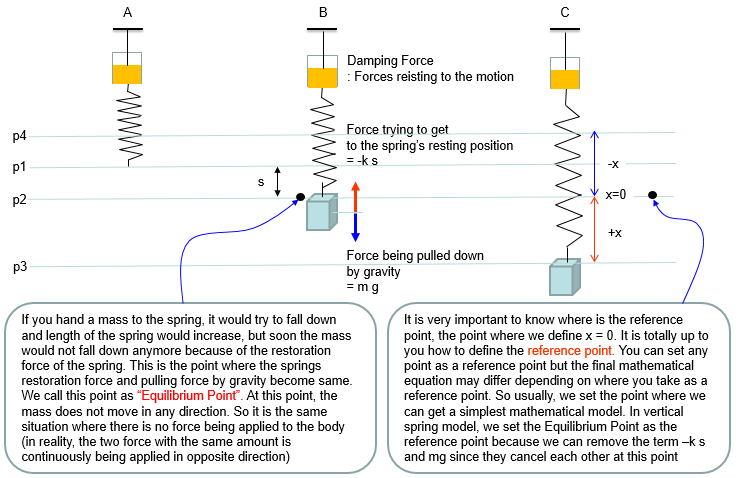
This example is just a small extention from the previous example. As I mentioned above, the previous example is about an ideal case where there is nothing that opposes (resists) the motion of spring or mass. In this example, we just add a small components that make the system more like real life system. In real life spring, there is always some factors that is opposing the spring movement (contraction and expansion) as if there is always some kind of frictions when you move any object(a mass) on a surface (e.g, table). This kind of opposing factor in the spring syste is called Damping. As you cannot completely remove the friction on a surface, you cannot completely remove this kind damping however hard you try. In some case (e.g, in shock absorbers in mortor bike or automatives), we physically add special components that increases this kind of damping, So in real life modeling of a spring system, the first additional component to be added to the idea model would be a damper. Usually a damper is illustrated as shown below (looks like a very simple piston).
Based on the governing equation for this system, you would be able to list up all the component forces acting upon the system as shown below. You would notice that most of the component factors are same as previous example. The only difference is that a damping force is added to the equation.
Combining these two parts you will get the equation as (1) and with a little bit of rearrangement you will get the equation as (2). You may ask "Do I have to rearrange (1) always ?". The answer is NO. The equation (1) and (2) are completely same. The physical interpretation of (1) and (2) may vary a little bit, but mathemtically they are same. You will see both forms for the exactly same physical model in various material(e.g, textbook, internet etc).
< Example : Simple Harmonic Motion - Vertical Motion with Damping and External Force >
< Simple Harmonic Motion - Horizontal Motion - No Damping >
This example is also a kind of ideal case as in the first example. It is assumed that there is no friction on the surface and no damping on the spring. The only difference is that the spring and mass lies in horizontal direction and the object is moving in horizontal direction.
Governing equation is same as in previous example (i.e, based on Newton's second law). But you would notice that the list of factors (forces) applied to the mass is much simpler than the case in previous example. It is becase we don't have to worry about the gravitation forcess in this ideal system.
Combining these two parts you will get the equation as (1) and with a little bit of rearrangement you will get the equation as (2). You may ask "Do I have to rearrange (1) always ?". The answer is NO. The equation (1) and (2) are completely same. The physical interpretation of (1) and (2) may vary a little bit, but mathemtically they are same. You will see both forms for the exactly same physical model in various material(e.g, textbook, internet etc).
NOTE : I put the graphical solution of this equation in my visual note visual note. You can check how the solution changes as the parameters in the equations varies as listed below.
< Simple Harmonic Motion - Horizontal Motion - with Damping >
This example is a little bit of extention to the previous one. In this condition, we assume that the spring experience damping as it moves.
Governing equation is same as in previous example (i.e, based on Newton's second law). You see that one additional factor (damping) is added here.
Combining these two parts you will get the equation as (1) and with a little bit of rearrangement you will get the equation as (2). You may ask "Do I have to rearrange (1) always ?". The answer is NO. The equation (1) and (2) are completely same. The physical interpretation of (1) and (2) may vary a little bit, but mathemtically they are same. You will see both forms for the exactly same physical model in various material(e.g, textbook, internet etc).
NOTE : I put the graphical solution of this equation in my visual note visual note. You can check how the solution changes as the parameters in the equations varies as listed below.
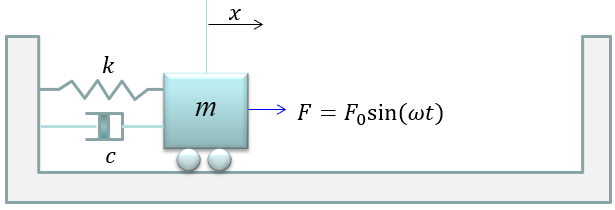
Single Spring with External Force
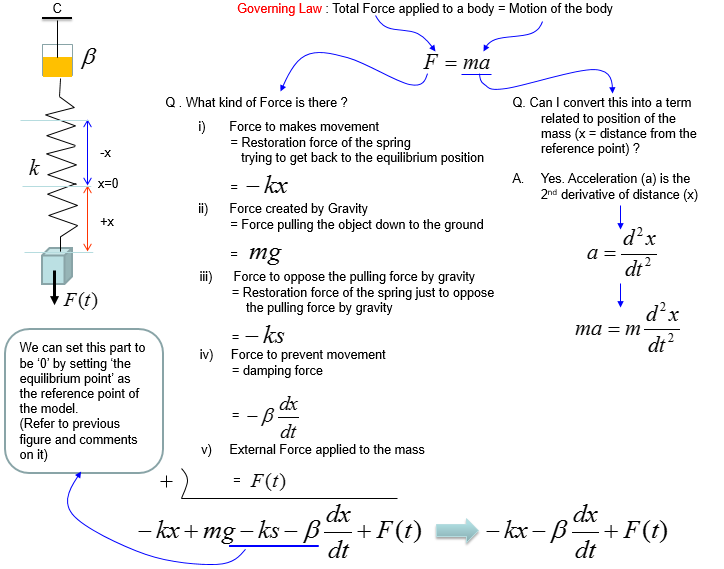
This example is a little bit of extention to the previous one. In this condition, we assume the cases where some external forces acting upon the mass. I think this can be an example with almost all the essential component/factors of a spring mass system. You see the mass, damping, spring coefficient and external force. In theory, by combining (concatenating) this fundmental component you would be simulate almost any form of dynamic system.
You can think of external forces in many different pattern. In this example, I assume that the external force is in the form of sinosoidal which means it is changing at certain periodicity and amplitude.
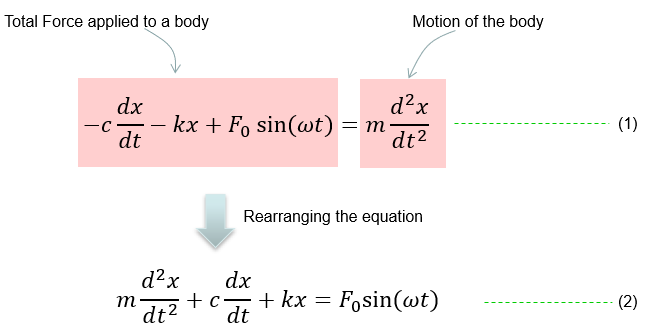
Governing equation is same as in previous example (i.e, based on Newton's second law). You see that one additional factor (External Force) is added here.
Combining these two parts you will get the equation as (1) and with a little bit of rearrangement you will get the equation as (2). You may ask "Do I have to rearrange (1) always ?". The answer is NO. The equation (1) and (2) are completely same. The physical interpretation of (1) and (2) may vary a little bit, but mathemtically they are same. You will see both forms for the exactly same physical model in various material(e.g, textbook, internet etc).
NOTE : I put the graphical solution of this equation in my visual note. You can check how the solution changes as the parameters in the equations varies as listed below. One thing I want to emphasize about the solution of this equation (i.e, the behavior of the motion) is that it would show the much complicated pattern comparing to the case without the external force. With this kind of perodic external force, the system would show an interesting behavior called 'Resonance'. I will write a seprate note about resonance later.. for now I would recommend you to look into some of the solution of this equation association with frequency response.
Matlab Solution for Single Spring System
In this example, you have learned how to model the motion of a mass tied to a vertical spring. From this very simple example, you can extend to more and more complicated situation which is closer to real engineering example. Following would be general steps on how to extend this simple spring model to more complicated situation (There are no detailed explanation about the modeling process. It would just give you the differential equation and show how the solution of the equation look like, but I hope you would not have much difficulties understand the equations). First two are the one you saw in this example, but I listed here to show you how the solution look like.
Example : Coupled Spring (Multi Spring)
The examples in this section will be very usefull to model various mechanical system. You would say "This is just two springs or three springs connected to each other.. doesn't look like very useful". But there are many mechanical problems that can be described in the form of multiple masses connected to each other with springs. For example, you can model an entire automobiles with several hundreds masses connected to each other by several undreds springs and can analyze how the each parts of the whole car vibrate when you drive it along a bumpy road. You may think this kind of simple two or three spring model is not related to such a complicated model for the entire car, but in reality the logic and process of modeling is exactly same. You would just have several dozens of differential equations in stead of two or three equeations, which is very similar to what you see here. Don't worry about solving a system differential equation which is made up of several hundred equations. Nobody do it by hand. There is a lot of computer tools to do this. Your job is to fill in the parameters or sometimes mathmatical equations to such tools and to do that you have to understand the meaning/logics of the mathematical model.
< Example : Two Masses coupled three springs without damping >
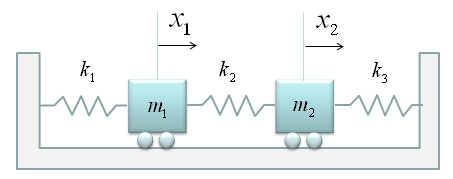
Now let's look into a little bit more complex spring model as shown below.
At the first look, you may be overwhelmed by the complexity of the situation. But don't be scared, there is an easy way to do the modeling for this kind. The trick is to split the problem into multiple single spring situation. Then you can use the logic that you have learned in the single spring model. (Note : This is a model which may be simpler than the real life system. First, you don't see any external forces applied to any of the mass. Also, you don't see any friction (or damping) is applied to the mass. It means the movement of the mass is only determined by spring force).
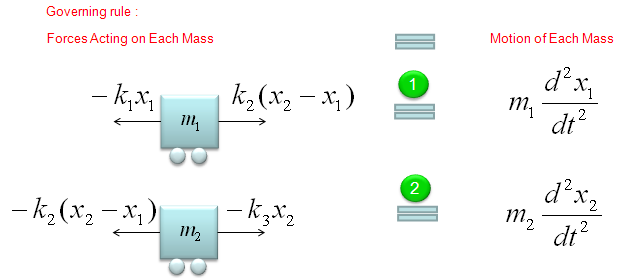
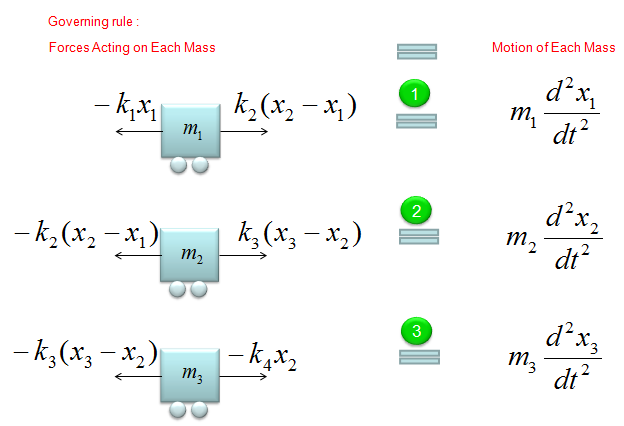
In this example, we can split the whole system into following two single spring model. As you see, the governing rule is same as the one we saw in the single spring model. (If you get familiar with this kind of splitting method, you can easily do the modeling for a system with even 100 mass/springs. Logic would be the same. You would get 100 differential equations of single spring-mass. that's it). I think the biggest question you may have at this point is how the sign of each component equation is determined ? That is, why some part has 'negative' sign and some other parts does not have the negative sign ? (This is super.. super ... super .. important.. but not easy to explain in simple manner. So I created a separate post for this. Refer to 'How each the sign of each component terms are determined ?' )
If you can draw a diagram as shown above and express the behavior of each component in a mathmatical form, it is the end of modeling. You already complete the modeling of this system. But to convert the model into a set of differential equations that is familiar to us, let's rearrange the each of the mathematical components.
Let's start with the model for the first mass-spring component. Actually the first line can express the physical meaning of the model the best, but for mathematical convinience or for applying other analytic method, we often do this kind of rearrangement, but there is no single best expression. if you see various textbooks, you would notice that everybody would use a little bit different format. So just pick one of this form and trying to memorize it would not have any practical use.. try to understand the meaning of each component in stead of memorizing the equation.
Let's start with the model for the second mass-spring component. A
Through the process described above, now we got two differential equations and the solution of this two-spring (couple spring) problem is to figure out x1(t), x2(t) out of the following simultaneous differential equations (system equation).
This is the end of modeling. But some textbook likes to express this kind of simultaneous equations into a matrix form as follows. This is just a different ways of expression but sometimes looks very intimidating. (This is just a psychological issues that I mentioned the introduction page).
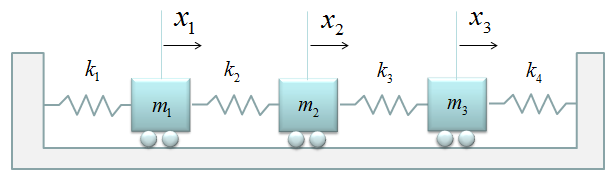
< Example : Three Masses coupled with Four springs without Damping >
Not let's add another Spring-Mass to make it three mass with four springs. You may ask "Until when you will keep adding like this ? Are you going to make 100 examples for these ? Please be patient. We are almost reaching the destination.
Now just summerize the governing equations for each of the masses. It would look as follows.
Now we need to create a system equation from the set of governing equations, but I would not go through this process step-by-step. Please try on your own to make yourself more familiar with the process. The result would look as follows.
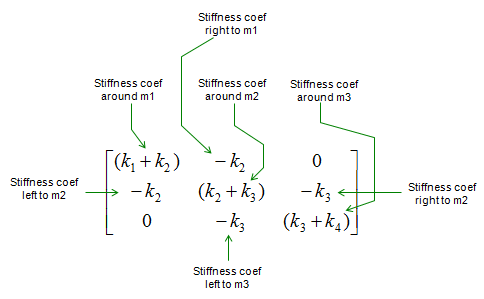
Now let's look into the matrix K more detail and try to see if there is any recognizable pattern. Try to find out pattern on your own before you see the answer. The answer is as follows.
If you gets familiar with this pattern, you don't even think about all the detailed/tedious procedure you went through in previous examples. Your finger can create these matrix mechanically. You can even create a small program to create these matrix even though you are not an expert programmer.
NOTE : You may construct the Stiffness Coefficient matrix just by applyting the technique to construct the Stiffness matrix instead of deriving the whole differential equation.
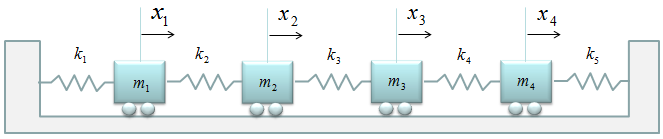
< Example : Four Masses coupled Five Springs without Damping >
Now let's add one more Spring-Mass to make it 4 masses and 5 springs connected as shown below.
Now let's summarize the governing equation for each of the mass and create the differential equation for each of the mass-spring and combine them into a system matrix. Do you really want me to do this ? No worries.. it is just kidding. I just want you to apply the pattern that you saw in previous example. You can easily(?) get the following system equation.(If this is not easy for you, look into the illustration showing the pattern in previous example).
NOTE : You may construct the Stiffness Coefficient matrix just by applyting the technique to construct the Stiffness matrix instead of deriving the whole differential equation.
< Example : N coupled spring without Damping >
You would yell at me if I ask you to build the system equation by going through the governing equation for each of the spring-mass. of the following Spring-Mass System
However, you can build the system equation if you apply the pattern that you saw in previous example. I know it would take long time, but it would not drive you crazy. If you have anlalyzed the logics (patterns) of the matrix shown in previous example, you may (I hope) construct the N x N matrix as shown below.
NOTE : You may construct the Stiffness Coefficient matrix just by applyting the technique to construct the Stiffness matrix instead of deriving the whole differential equation.
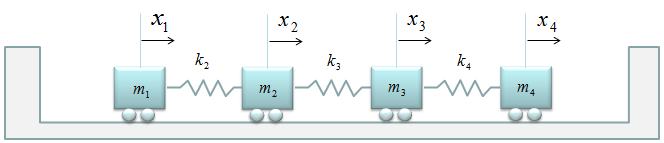
< Example : Four Masses coupled spring with Free Ends without Damping >
What if we have the coupled spring system as shown below. It would look almost the same as we saw in previous example. If you look carefully into it, you will notice that the first and last spring has open end which is not tied to the wall.
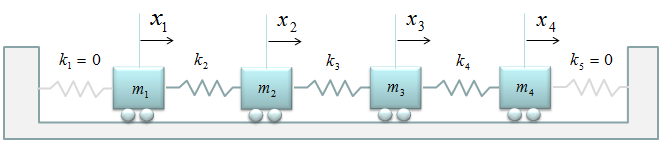
If you are trying to create the governining equations for each mass from scratch, you may feel some difficulties to create the differential equation for the first and last spring since it is new pattern for you. But if you think this problem from just a little bit different perspective, you will realize that this is also exactly same problem as you saw in previous examples. Just replace the open ends with a spring which has k = 0 as shown below.
With this small modification and the matrix creation pattern you saw in previous example, you can build the system equation within one minute. Just plug 0 into k1 and k5.
And you will get answer as shown below.
NOTE : You may construct the Stiffness Coefficient matrix just by applyting the technique to construct the Stiffness matrix instead of deriving the whole differential equation.
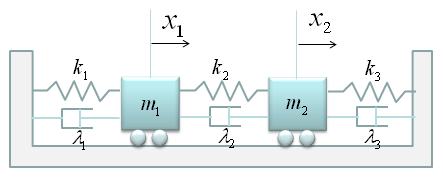
< Example : Single Mass and Two spring with Common Damping >
< Example : Two Mass and Three spring with Damping >
This example is just half step extension of previous example. It is made up of two mass and three springs which is the same as in previous example. The only difference is that damping factors are introduced as shown below.
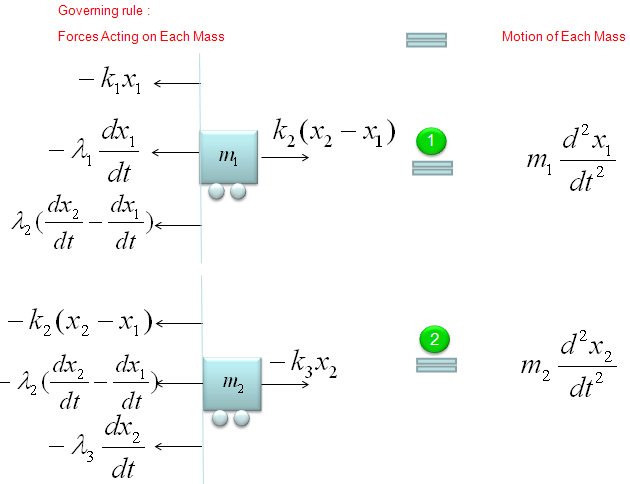
If you have followed through the previous examples, you may know what to do by now. i) Split the given model into each component ii) Define the governing rules for each component. This is the procedure for any kind of mathemtical modeling.
The governing rule of the first component is as follows. Overall logic is i) Define all the forces being applied to the object ii) Draw arrows represending the direction of the force (Be very careful of determining the direction of arrows since it determines the sign of the mathematical term) iii) Write the mathematical formula to each of the forces (arrows)
Next step is to combine all the mathematical components of each arrow and the motion of the movement into a single equation as follows. The first line is the orginal form. All the other lines are just rearrangement of the first line, so mathematically they are all same. You can just pick whatever you want for your needs/preference, but the last one and the second-to-the-last one are the most common forms.
Do the same thing for the second component as shown below.
Now we have two differential equations for two mass (component of the system) and let's just combine the two equations into a system equations (simultaenous equations) as shown below.
In most cases and in purely mathematical terms, this system equation is all you need and this is the end of the modeling. But in some case you may want to convert these system equations into a set of the first order equations as follows. (If you are not familiar with this kind of conversion process, refer to Converting High Order Differential Equation into First Order Simultaneous Differential Equation)
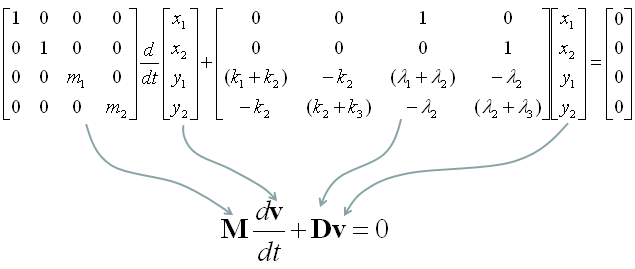
Once you have a set of differential equation which are all first order, you can easily convert it in the form of Matrix equation as shown below. (If you are not familiar with this kind of conversion, refer to Differential Equation meeting Matrix)
Example : Inverted Spring System
< Example : Inverted Spring-Mass with Damping >
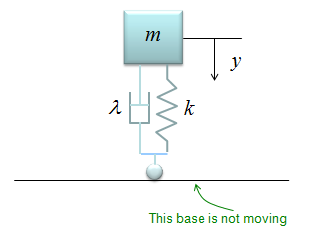
Now let's look at a simple, but realistic case. Let's assume that a car is moving on the perfactly smooth road. This can be illustrated as follows. The body of the car is represented as m, and the suspension system is represented as a damper and spring as shown below. (Note: You may ask why the gravitational force being applied to the mass is not considered here. It is because of the assupmtion that the equilibrium point is set so that the gravitational force is cancelled out. See the Simple Spring example about the equilibrim point)
The differential equation can be represented as shown below. I will not describe the steps to come up with this equation. Try yourself to figure out how to derive this equation based on previous examples. You would not have much difficulties for it.
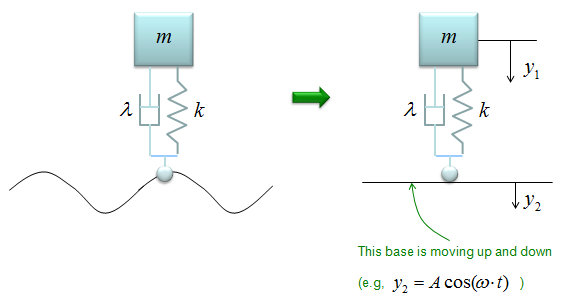
< Example : Inverted Spring-Mass with Damping and Moving Base Line >
This example is similar to previous example, but has one additional factor. In this example, the car is not moving along a smooth road. it is moving a long a bumpy road as illustrated on the left side. This can be modeled in a similar way to the previous example except that the base line is moving as illustrated on the right side.
The differential equation can be represented as shown below. I will not describe the steps to come up with this equation. Try yourself to figure out how to derive this equation based on previous examples. You would not have much difficulties for it. You would notice that another displace variable y2 is introduced in this equation.
If the car is moving on perfectly harmonic surface, the y2 can be expressed as a trigonometric function (e.g, cos(w t)) and the w can be determined by the speed of the car. So with this equation, you can figure out how the body of the car will move up and down when the car is moving on a bumpy road with a certain velocity.
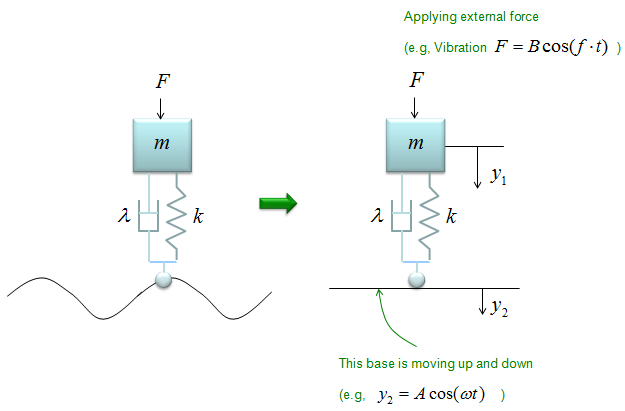
< Example : Inverted Spring-Mass with Damping and Moving Base Line and External Force>
This example is similar to previous example, but has one additional factor. In this example, the car is moving along a bumpy road and it also is under some external force. (In most case, the car is experencing various internal vibration and the vibration can be a kind of external force). This can be modeled in a similar way to the previous example except that the base line is moving as illustrated on the right side.
The differential equation can be represented as shown below. I will not describe the steps to come up with this equation. Try yourself to figure out how to derive this equation based on previous examples. You would not have much difficulties for it. You would notice that another displace variable y2 is introduced in this equation.
If the car is vibrating in a harmonic function with a certain frequency and the F can be expressed as a trigonometric function (e.g, cos(f t)). So with this equation, you can figure out how the body of the car will move up and down when the car is moving on a bumpy road with a certain velocity and the body is also expericing vibration.
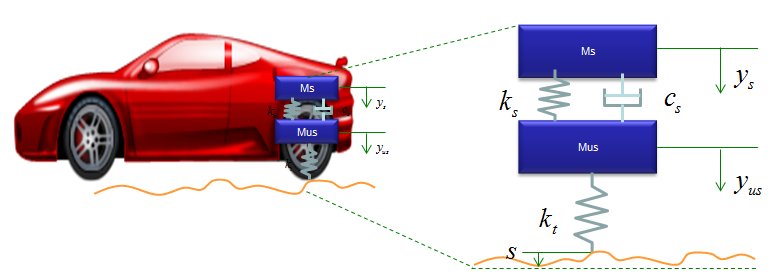
< Example : Inverted Spring - Quarter Car Model (Car Suspension for hone wheel) >
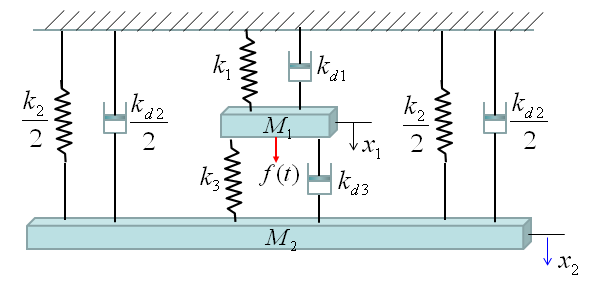
< Example : Coupled spring - Vehicle Suspension System >
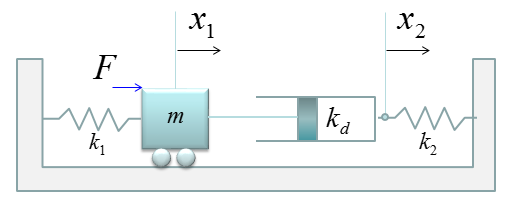
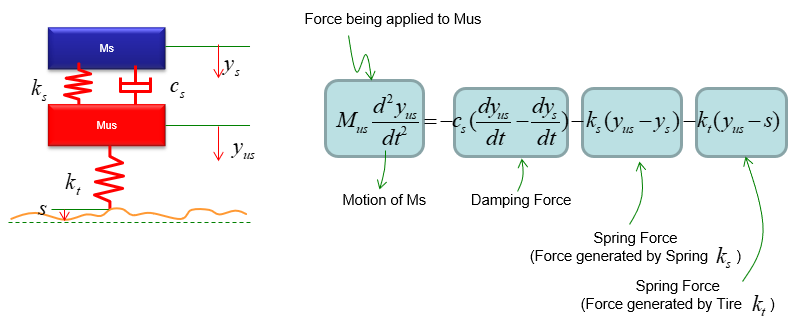
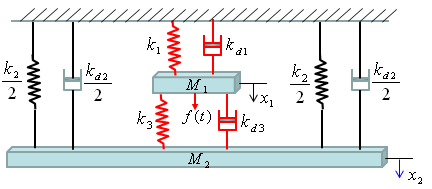
You can practice what you learned from the previous two examples and this is the one that can be easily extended for a real life problem. You can easily apply this example to model a suspension system of a vehicle. It may look a little bit scary, but the logic of the modeling is always the same however complex system it is. Do you remember the logic (process) ? i) Break down the system into each component. (When you see this kind of spring-mass system, each Mass is the building block of the system). ii) Draw the arrows (vectors) to represent the direction of Forces being applied to each component. iii) Write down mathematical formula for each of the arrows (vectors). iv) Combine all the component formula into a single differential equation
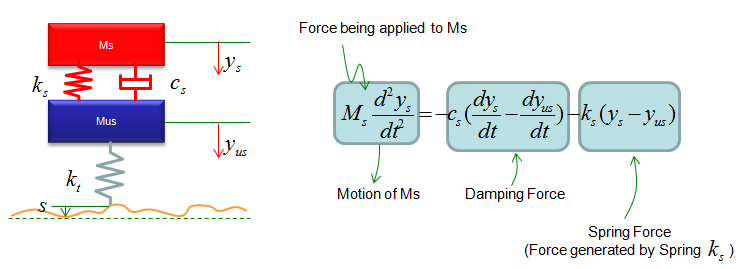
Now Let's start with the first component. Can you identify the component ? M1 is the first component. Mark all the springs, damper and applied force for the component as shown below.
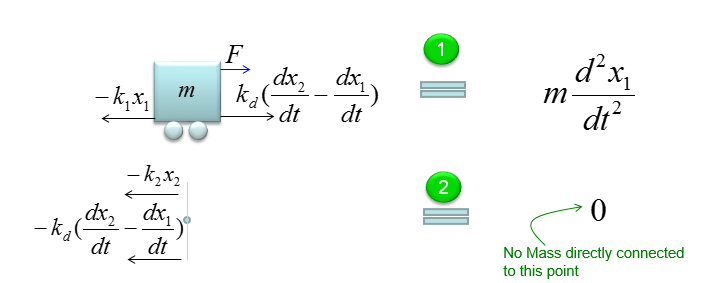
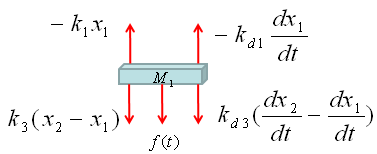
Now draw arrows (vectors) to represent forces being aplied to the component (Mass) as shown below.
Now combine each component formula into single differential equation as shown below.
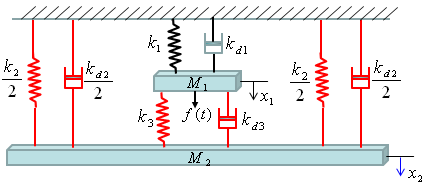
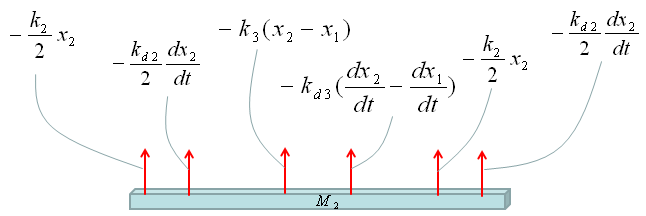
Now Let's start with the second component. Can you identify the component ? M2 is the first component. Mark all the springs, damper and applied force for the component as shown below.
Now draw arrows (vectors) to represent forces being aplied to the component (Mass) as shown below.
Now combine each component formula into single differential equation as shown below.
With a little bit of operation, you can simplify the equation into the one as follows.
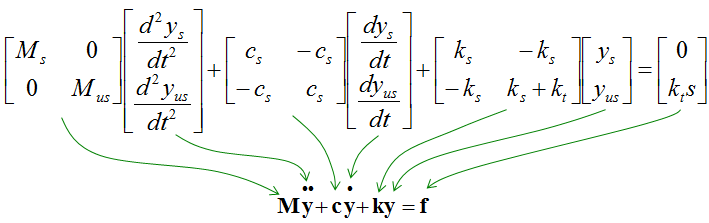
If you combine the equation for component 1 and component 2, you would get a system equation as follows.
I wouldn't do this here, but I recommend you to try to convert this into a matrix form. It will be a good practice for first order conversion and matrix form conversion.
More Readings
|
||