I would say to many of friends and juniors working in engineering area "If you are good at two topics, Matrix and Differential Equations, you would be good at ANY of the engineering field." Of course, just being good at math would not automatically lead you to success in the field, but we cannot deny the fact that mathematical understanding is very crucial in most of engineering. In this page, I would like to explain the basic concept of differential equation and it's applications as easy as I can do, but in some cases it is hard to avoid tackling the mathematical equations directly.

• What is Differential Equation ?
• Difference between Differential Equation and Algebraic Equation
• Various Way of Presentation
• Terminology and Classification
• Why Differential Equation ?

What is Differential Equation ?

Let's start from the name itself. A differential equation is an ordinary equation with one extra ingredient. Everything else on this page depends on seeing that ingredient clearly.

Just putting the question in a little bit different way, we can get the answer to this question as follows.

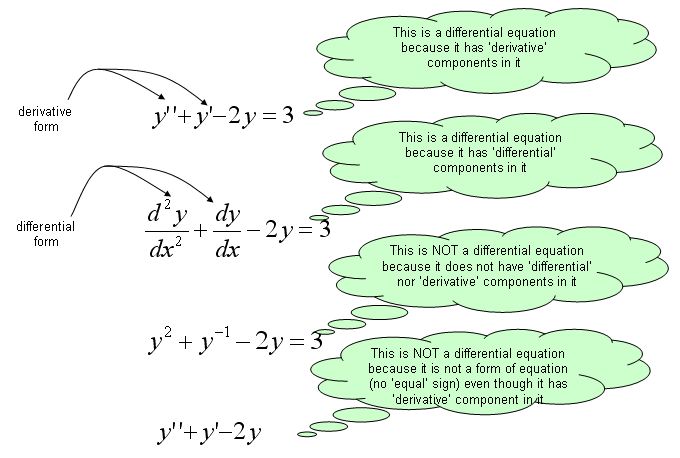
Differential Equation is a kind of Equation that has a or more 'differential form' of components within it.

Somebody say as follows. (This is exactly same as stated above).

Differential equation is an equation that has derivatives in it.

As you see here, you only have to know the two keywords 'Equation' and 'Differential form (derivatives)'.

Let's think about the first keyword 'Equation'. What is an Equation ? You can find so many different type of definition of Equation from various text books and pages from internet. One of the definition/explanation that I found the best is from a math site for elementary school student (http://www.mathsisfun.com/algebra/equation-formula.html)

An equation says that two things are equal. It will have an equals sign "=" like this:

x + 2 = 6

That equations says: what is on the left (x + 2) is equal to what is on the right (6)

So an equation is like a statement "this equals that"

According to this definition,  3 + 5 = 8 type of statement is also an Equation. But this kind of equation is not much of our interest. The type of equation that we are interested is the equation that has one or more variables (unknown values) as shown in the definition above.

For example, x + 2 = 6. 'x' is the unknown value in the equation. Solving the equation means 'finding the value for the variable' which satisfies the equation.

Now let's think about the second keyword, derivative (differential form). Unfortunately, you would not find such a nice definition as above from elementary school website because they don't learn it -:). So I would like to quote a definition from Wikipedia as follows. (http://en.wikipedia.org/wiki/Derivative)

the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a moving object with respect to time is the object's instantaneous velocity

Considering that derivative is expressed in the form of dy/dt or y' or df/dt, f'(t) etc. So differential equation can be described as any equation that contains components of dy/dt or y', y'', f'(t) etc.

The diagram below tests four expressions against the two keywords. Two of them pass. Each of the other two fails on a different keyword.

An expression is a differential equation only when it has both an equals sign and a derivative.

• The first two are the same equation : y'' + y' - 2y = 3 and d²y/dx² + dy/dx - 2y = 3 differ only in notation. The derivative form uses primes, and the differential form uses d/dx.
• The third fails on the derivative : y² + y^-1 - 2y = 3 has powers of y but no rate of change. So it is an algebraic equation.
• The fourth fails on the equation : y'' + y' - 2y has derivatives but no equals sign. It is an expression, and there is nothing to solve.

Difference between Differential Equation and Algebraic Equation

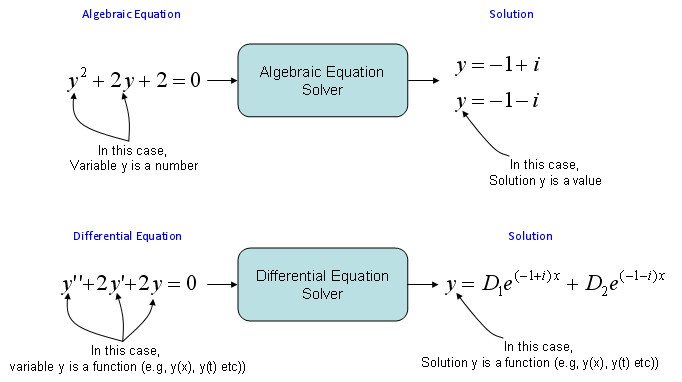
I think you would know what is Algebaic Equation. You may not be able to explain exactly what it is, but I am pretty sure that you would have some intuitive understandings on what is the algebraic equation.

One of the best way to learn a new area is to compare the new concept with the concepts which you are already familiar with.

Algebraic equation is to describe a relationship among multiple 'Numbers' and 'Finding the solutions' to an Algebraic equations is to 'find Numbers' that satisfy the equation.

Differential equation is to describe a relationship among multiple 'Functions' and 'Finding the solutions' to a Differential equations is to 'find Functions' that satisfy the equation.

The diagram below puts the two kinds of equation side by side. Both use the same coefficients 1, 2 and 2, which makes the link between them easy to see.

An algebraic equation is solved by numbers, and a differential equation is solved by functions.

• The same numbers appear in both solutions : y² + 2y + 2 = 0 has the roots -1 + i and -1 - i. The same two numbers appear in the exponents of the solution to the differential equation.
• This is not a coincidence : try y = e^rx in y'' + 2y' + 2y = 0. Each derivative brings down one factor of r, so the equation becomes (r² + 2r + 2) e^rx = 0. Because e^rx is never zero, r must solve the algebraic equation above. This is called the characteristic equation.
• A differential equation has a family of solutions : the constants D₁ and D₂ can take any value. A second-order equation needs two extra conditions, such as y(0) and y'(0), to pick one member of the family.
• The same solution in real form : by Euler's formula, the two complex exponentials combine into y = e^-x(C₁ cos x + C₂ sin x). This is a decaying oscillation, the same shape a damped spring or an RLC circuit shows.

Various Way of Presentation

The same differential equation can be written in several ways. Textbooks, papers and software tools each prefer a different one. So you need to recognise all of them as the same equation before going further.

The picture below names the parts of a function written as y(t). Every form that follows is built from these parts.

A function prototype names the dependent variable and the independent variable together.

• The two variable labels are swapped in the picture : y is the dependent variable, because its value depends on t. t is the independent variable, the one you choose freely. The order illustration in the Terminology section labels them the right way round, with y(x).
• The prototype carries both names : writing y(t) states the dependent variable and the independent variable at the same time. The shorter forms below drop one or both.

The picture below writes one third-order linear equation in four ways, from the most detailed form to the most compact one.

All four lines are the same equation. They differ only in how much of the notation they spell out.

• Forms 1 and 2 use Leibniz notation : dⁿy/dtⁿ names both variables. So it is the safest form when more than one independent variable is around.
• Form 3 uses prime notation : y', y'' and y''' leave the independent variable implicit. You have to know from the context whether it is t or x.
• Form 4 uses dot notation : a dot means a derivative with respect to time only. Physics and control texts use it for motion, where the independent variable is always t.
• The coefficients do not change : a₂, a₁ and a₀ are the same in every form. So moving between the forms is only a change of notation.

Terminology and Classification

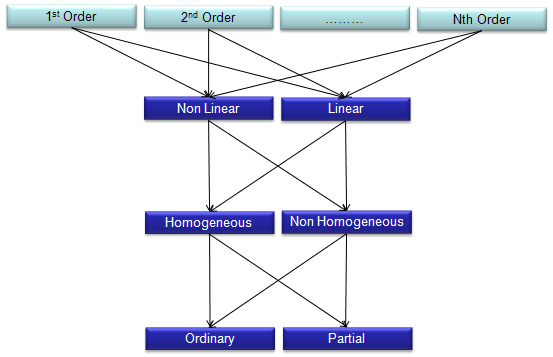
One of the things that made me feel very confused (difficult) about the differential equation when I first read books were that there are so many different types of differential equations and I got confused with just those names, not to mention of solving the equations.

After struggling for long time, I came out with a couple of criteria that helps me a little bit clearer understandings of classification as illustrated below. If you just follow the path from the top to the bottom, you would get all the possible types of differential equations.. at least those names -:)

For example, you can follow through these arrows and come up with followings

• 1st order linear homogeneous ordinary differential equation
• 2nd order non-linear homogeneous ordinary differential equation
• 3rd order non-linear non-homogeneous ordinary differential equations
• ....

Why do we have to care about these classification and the confusing names ?

Unfortunately there is no single method that can solve all different types of differential equations. If you see the text books, there is specific method for the specific types. This naming/classification would be very helpful for you to find proper method for those equations given to you.

• Linear has a precise meaning : y and its derivatives appear only to the first power, and they are never multiplied together. The coefficients may depend on the independent variable. For example, y'' + x y = 0 is linear, while y'' + y² = 0 and y y' = 1 are not.
• Homogeneous is normally defined for linear equations : the test in the homogeneous illustration below looks for a term r(x) with no y in it. That test only makes sense once the equation is linear. So a name such as non-linear homogeneous is rarely used. Some textbooks also use homogeneous in a different sense for first-order equations.

Now let's look into the meaning of each word in this classification path.

'Order' of a differential equation is explained in the following illustration.

Homogeneous and Non-Homogeneous differential equations are defined as follows.

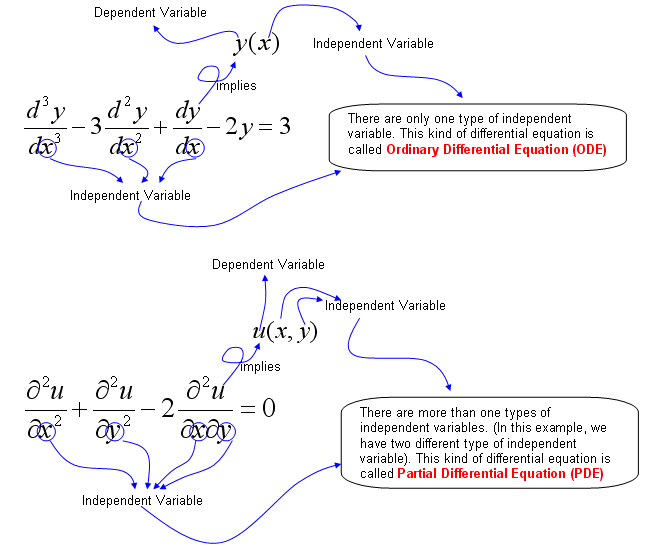
The difference between Ordinary differential equation and partial differential equation is explained in the following illustration.

Why Differential Equation ?

So far the page has shown what a differential equation looks like. This section answers the practical question behind it: why engineers write their problems in this form at all.

Why we do the mathematical modeling ?

It is to predict something based on the rules of changes of a system.

Here we have two important tems marked in red, "predict" and "rules of changes".

Let's think about the first term "predict". What is definition of "predict" ? Two definitions that I found in internet are as follows.

• A prediction is a statement about the way things will happen in the future
• Say or estimate that (a specified thing) will happen in the future or will be a consequence of something.

In plain terms, 'predict', 'prediction' is to figure out NOW something that will happen in the FUTURE.

For this kind of prediction, we need some 'information' or 'knowledge' ? To predict something without any information or knowledge is impossible at least in science and engineering area. (It may be possible to predict something without any background information in fortune telling, but it is not called 'science' or 'engineering).

Then what do you mean by 'information' or 'knowledge' ?

Information (Knowledge) in this context is "rules of changes" for the things that we want to predict.

The "rules of changes" is given in most case in the form of "If something changes over time like this", "If something changes over space".

Now we have two critical terms to describe the background information for prediction

i) changes over time

ii) changes over space

as you would know, if we just convert these statement into mathmatical form it becomes as follows

i) changes over time = d (something)/dt

ii) changes over space = d (something)/dx

So the most of the prediction problem is given as follows.

i) If d (something)/dt = an expression(description), what will happend to the 'something' in the future ?

ii) If d (something)/dx = an expression(description), what will happend to the 'something' at the point which is far away from here ?

If you just convert the statements above into a mathematical form, it is a differential equation.  I hope you got my point now.

Here is a small example. Newton's law of cooling says that a cup of coffee loses heat at a rate proportional to its temperature difference from the room. Let T be the coffee temperature and T_a the room temperature. Then the rule of change is dT/dt = -k(T - T_a). Solving it gives T(t) = T_a + (T₀ - T_a) e^-kt, where T₀ is the starting temperature. Take coffee at 90 degrees C in a 20 degrees C room, with k = 0.1 per minute. The prediction after 10 minutes is 20 + 70e^-1, about 45.8 degrees C.

• A differential equation states the rule of change : it says how fast something changes, not what its value is.
• Solving it turns the rule into a prediction : the solution gives the value at any future time or at any distant point.
• A starting value is always needed : the same rule with a different T₀ gives a different future. That is why every prediction problem comes with initial or boundary conditions.