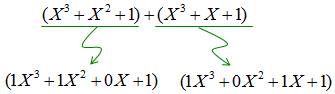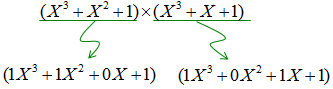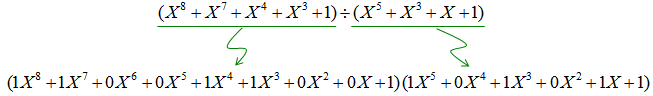Communication Technology

GF(2) : Galois Field 2

Galois Field is a term that is made up of 'Galois' (name of a person) and 'Field' (a mathematical term).  Galois Field is a kind of Field that is contains a finite number of elements. Explaining about 'What is Field' is not a scope of this page. To be honest, I don't have enough mathematical knowledge to describe the concept of Field in my own words.

GF(2) represents a kind of Galois Field that is made up of only two elements 0 and 1. It can be represented in mathematical term as follows.

You can think of GF(2) as a special mathematical tools that explains various properties of binary operation (mathematical operations about binary numbers). The reason why this is important in communication is that the digital communication is based on binary data and various mathematical operations dealing with binary numbers. You wouldn't see this term on every day job in communication engineering, but many technologies (especially 'coding' techniques) are based on this theory even though you are not aware of it.

Some important rules (properties) of GF(2) can be summarized as follows. Simply put, the two most common operation is GF(2) is 'Addition' and 'Multiplication'. These two operations are defined as follows.

In most applications of GF(2), we represents a binary data into polynomials (Galois polynomials) and do various operations on those polynomials.  Rather than explaining too much, just going throug several examples would be more helpful.

Examples :

• Example 1 : Addition of GF(2) Polynomial

• Example 2 : Multiplication of GF(2) Polynomial

• Example 3 : Division of GF(2) Polynomial

• Example 4 : Application of GF(2) - CRC Checksum Bit Calculation

Example 1 : Addition of GF(2) Polynomial >

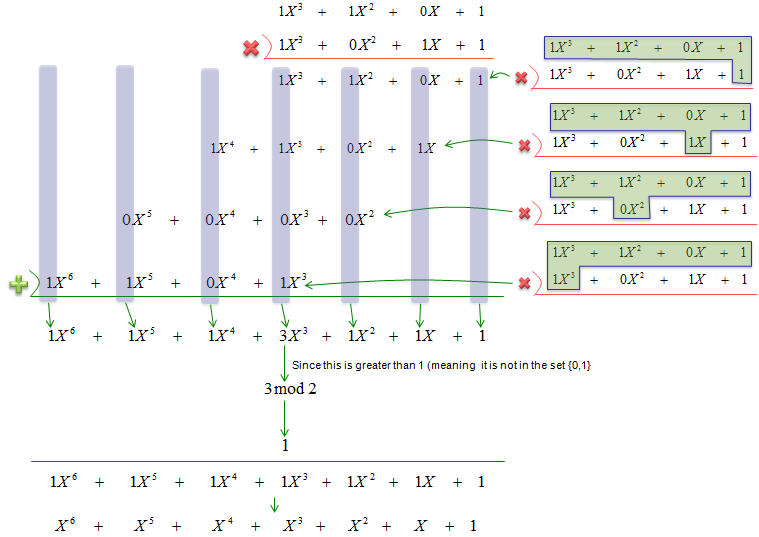
Example 2 : Multiplication of GF(2) Polynomial >

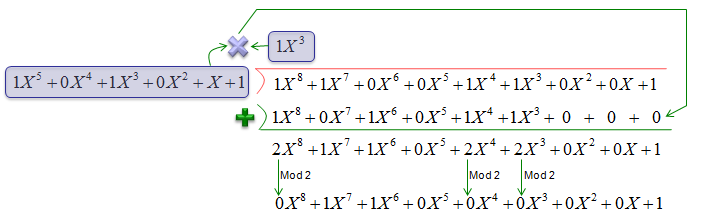
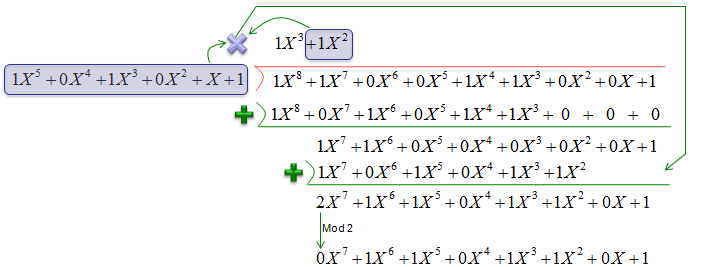
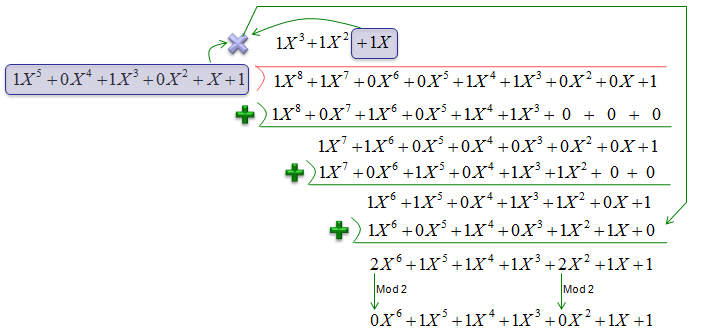
Example 3 : Division of GF(2) Polynomial >

NOTE : In this process, you see the following operations. This two step operation is same as 'XOR' in binary number. In real compuation (especially in digital process, 'XOR' is used in stead of this kind of two step process).

Step 1 : Add coefficient values for each term

Step 2 : If the added value is less then 2 (i.e, 0 or 1), write the number as it is. If the added value is 2, apply 'mod 2' to the numbr (i.e, if the value is 2, change the number to 0).

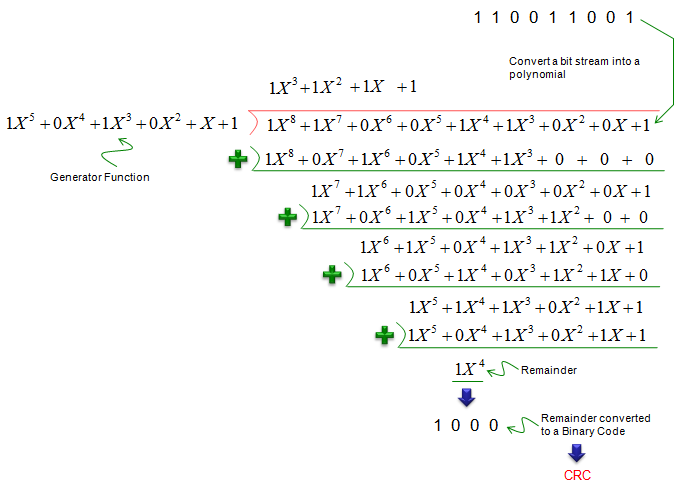
Example 4 : Application of GF(2) - CRC Checksum Bit Calculation >